Цифровые схемы - Краткое руководство
Если основание или основание системы счисления - 'r', тогда числа, присутствующие в этой системе счисления, находятся в диапазоне от нуля до r-1. Общее количество чисел в этой системе счисления - "r". Итак, мы получим различные системы счисления, выбирая значения системы счисления больше или равные двум.
В этой главе давайте обсудим popular number systemsи как представить число в соответствующей системе счисления. Наиболее часто используются следующие системы счисления.
- Десятичная система счисления
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричная система счисления
Десятичная система счисления
В base или основание десятичной системы счисления 10. Итак, в этой системе счисления используются числа от 0 до 9. Часть числа, лежащая слева отdecimal pointназывается целой частью. Точно так же часть числа, которая находится справа от десятичной точки, называется дробной частью.
В этой системе счисления последовательные позиции слева от десятичной точки имеют веса 10 0 , 10 1 , 10 2 , 10 3 и так далее. Точно так же последовательные позиции справа от десятичной точки имеют веса 10 -1 , 10 -2 , 10 -3 и так далее. Это означает, что каждая позиция имеет определенный вес, которыйpower of base 10
пример
Рассмотрим decimal number 1358.246. Целая часть этого числа - 1358, дробная часть - 0,246. Цифры 8, 5, 3 и 1 имеют веса 100, 101, 10 2 и 10 3 соответственно. Точно так же цифры 2, 4 и 6 имеют веса 10 -1 , 10 -2 и 10 -3 соответственно.
Mathematically, мы можем записать это как
1358,246 = (1 × 10 3 ) + (3 × 10 2 ) + (5 × 10 1 ) + (8 × 10 0 ) + (2 × 10 -1 ) +
(4 × 10 -2 ) + (6 × 10 -3 )
После упрощения членов с правой стороны мы получим десятичное число, которое находится слева.
Двоичная система счисления
Все цифровые схемы и системы используют эту двоичную систему счисления. Вbase или основание этой системы счисления 2. Итак, в этой системе счисления используются числа 0 и 1.
Часть числа, лежащая слева от binary pointназывается целой частью. Точно так же часть числа, которая находится справа от двоичной точки, называется дробной частью.
В этой системе счисления последовательные позиции слева от двоичной точки имеют веса 2 0 , 2 1 , 2 2 , 2 3 и так далее. Точно так же последовательные позиции справа от двоичной точки имеют веса 2-1 , 2-2 , 2-3 и так далее. Это означает, что каждая позиция имеет определенный вес, которыйpower of base 2.
пример
Рассмотрим binary number 1101.011. Целая часть этого числа - 1101, а дробная часть - 0,011. Цифры 1, 0, 1 и 1 целой части имеют веса 2 0 , 2 1 , 2 2 , 2 3 соответственно. Точно так же цифры 0, 1 и 1 дробной части имеют веса 2–1 , 2–2 , 2–3 соответственно.
Mathematically, мы можем записать это как
1101.011 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (0 × 2 -1 ) +
(1 × 2 -2 ) + (1 × 2 -3 )
После упрощения членов правой части мы получим десятичное число, которое является эквивалентом двоичного числа в левой части.
Восьмеричная система счисления
В base или основание восьмеричной системы счисления 8. Итак, в этой системе счисления используются числа от 0 до 7. Часть числа, лежащая слева отoctal pointназывается целой частью. Точно так же часть числа, которая находится справа от восьмеричной точки, называется дробной частью.
В этой системе счисления последовательные позиции слева от восьмеричной точки имеют веса 8 0 , 8 1 , 8 2 , 8 3 и так далее. Точно так же последовательные позиции справа от восьмеричной точки имеют веса 8 -1 , 8 -2 , 8 -3 и так далее. Это означает, что каждая позиция имеет определенный вес, которыйpower of base 8.
пример
Рассмотрим octal number 1457.236. Целая часть этого числа равна 1457, а дробная часть - 0,236. Цифры 7, 5, 4 и 1 имеют веса 8 0 , 8 1 , 8 2 и 8 3 соответственно. Точно так же цифры 2, 3 и 6 имеют веса 8-1 , 8-2 , 8-3 соответственно.
Mathematically, мы можем записать это как
1457,236 = (1 × 8 3 ) + (4 × 8 2 ) + (5 × 8 1 ) + (7 × 8 0 ) + (2 × 8 -1 ) +
(3 × 8 -2 ) + (6 × 8 -3 )
После упрощения членов правой части мы получим десятичное число, которое является эквивалентом восьмеричного числа в левой части.
Шестнадцатеричная система счисления
В base или основание шестнадцатеричной системы счисления 16. Итак, в этой системе счисления используются числа от 0 до 9 и буквы от A до F. Десятичный эквивалент шестнадцатеричных цифр от A до F - от 10 до 15.
Часть числа, лежащая слева от hexadecimal pointназывается целой частью. Точно так же часть числа, которая находится справа от десятичной шестнадцатеричной точки, называется дробной частью.
В этой системе счисления последовательные позиции слева от десятичной шестнадцатеричной точки имеют веса 16 0 , 16 1 , 16 2 , 16 3 и так далее. Аналогичным образом, последовательные позиции справа от десятичной шестнадцатеричной точки имеют веса 16 -1 , 16 -2 , 16 -3 и так далее. Это означает, что каждая позиция имеет определенный вес, которыйpower of base 16.
пример
Рассмотрим Hexa-decimal number 1A05.2C4. Целая часть этого числа - 1A05, а дробная часть - 0,2C4. Цифры 5, 0, A и 1 имеют веса 16 0 , 16 1 , 16 2 и 16 3 соответственно. Точно так же цифры 2, C и 4 имеют веса 16-1 , 16-2 и 16-3 соответственно.
Mathematically, мы можем записать это как
1A05.2C4 = (1 × 16 3 ) + (10 × 16 2 ) + (0 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 ) +
(12 × 16 -2 ) + (4 × 16 -3 )
После упрощения членов правой части мы получим десятичное число, которое эквивалентно шестнадцатеричному десятичному числу слева.
В предыдущей главе мы рассмотрели четыре известные системы счисления. В этой главе давайте переведем числа из одной системы счисления в другую, чтобы найти эквивалентное значение.
Преобразование десятичного числа в другое основание
Если десятичное число содержит как целую, так и дробную часть, тогда конвертируйте обе части десятичного числа в другую основу по отдельности. Выполните следующие действия для преобразования десятичного числа в эквивалентное ему число с основанием "r".
Делать division целой части десятичного числа и successive quotientsс основанием 'r' и запишите остаток, пока частное не станет равным нулю. Рассмотрим остатки в обратном порядке, чтобы получить целую часть эквивалентного числа по основанию 'r'. Это означает, что первый и последний остатки обозначают наименее значащую цифру и наиболее значительную цифру соответственно.
Делать multiplication дробной части десятичного числа и successive fractionsс основанием 'r' и записывайте перенос, пока результат не станет нулевым или не будет получено желаемое количество эквивалентных цифр. Рассмотрим обычную последовательность переноса, чтобы получить дробную часть эквивалентного числа по основанию 'r'.
Преобразование десятичного числа в двоичное
При преобразовании десятичного числа в его эквивалентное двоичное число выполняются следующие два типа операций.
- Деление целой части и последовательных частных с основанием 2.
- Умножение дробной части и последовательных дробей с основанием 2.
Example
Рассмотрим decimal number 58.25. Здесь целая часть равна 58, а дробная часть - 0,25.
Step 1 - Деление 58 и последовательные частные с основанием 2.
| Операция | Частное | Остаток |
|---|---|---|
| 58/2 | 29 | 0 (LSB) |
| 29/2 | 14 | 1 |
| 14/2 | 7 | 0 |
| 7/2 | 3 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1(MSB) |
⇒ (58) 10 = (111010) 2
Следовательно integer part эквивалентного двоичного числа 111010.
Step 2 - Умножение 0,25 и последовательных дробей с основанием 2.
| Операция | Результат | Нести |
|---|---|---|
| 0,25 х 2 | 0,5 | 0 |
| 0,5 х 2 | 1.0 | 1 |
| - | 0,0 | - |
⇒ (0,25) 10 = (0,01) 2
Следовательно fractional part эквивалентного двоичного числа .01
⇒ (58,25) 10 = (111010,01) 2
Следовательно binary equivalent десятичного числа 58,25 равно 111010,01.
Преобразование десятичных чисел в восьмеричные
При преобразовании десятичного числа в его эквивалентное восьмеричное число выполняются следующие два типа операций.
Деление целой части и последовательных частных с основанием 8.
Умножение дробной части и последовательных дробей с основанием 8.
Example
Рассмотрим decimal number 58.25. Здесь целая часть равна 58, а дробная часть - 0,25.
Step 1 - Деление 58 и последовательные частные с основанием 8.
| Операция | Частное | Остаток |
|---|---|---|
| 58/8 | 7 | 2 |
| 7/8 | 0 | 7 |
⇒ (58) 10 = (72) 8
Следовательно integer part эквивалентного восьмеричного числа 72.
Step 2 - Умножение 0,25 и последовательных дробей с основанием 8.
| Операция | Результат | Нести |
|---|---|---|
| 0,25 х 8 | 2,00 | 2 |
| - | 0,00 | - |
⇒ (0,25) 10 = (0,2) 8
Следовательно fractional part эквивалентного восьмеричного числа .2
⇒ (58,25) 10 = (72,2) 8
Следовательно octal equivalent десятичного числа 58,25 равно 72,2.
Преобразование десятичного числа в шестнадцатеричное
При преобразовании десятичного числа в его эквивалентное шестнадцатеричное число имеют место следующие два типа операций.
- Деление целой части и последовательных частных с основанием 16.
- Умножение дробной части и последовательных дробей с основанием 16.
Example
Рассмотрим decimal number 58.25. Здесь целая часть равна 58, а десятичная часть - 0,25.
Step 1 - Деление 58 и последовательные частные с основанием 16.
| Операция | Частное | Остаток |
|---|---|---|
| 58/16 | 3 | 10 = А |
| 3/16 | 0 | 3 |
⇒ (58) 10 = (3A) 16
Следовательно integer part эквивалентного шестнадцатеричного числа - 3А.
Step 2 - Умножение 0,25 и последовательных дробей с основанием 16.
| Операция | Результат | Нести |
|---|---|---|
| 0,25 х 16 | 4.00 | 4 |
| - | 0,00 | - |
⇒ (0,25) 10 = (0,4) 16
Следовательно fractional part эквивалентного шестнадцатеричного числа .4.
⇒(58.25)10 = (3A.4)16
Следовательно Hexa-decimal equivalent десятичного числа 58,25 равно 3A.4.
Преобразование двоичного числа в другие базы
Процесс преобразования числа из двоичного в десятичное отличается от процесса преобразования двоичного числа в другие основания. Теперь давайте обсудим преобразование двоичного числа в десятичную, восьмеричную и шестнадцатеричную системы счисления по очереди.
Преобразование двоичного числа в десятичное
Для преобразования двоичного числа в его эквивалентное десятичное число сначала умножьте биты двоичного числа на соответствующие позиционные веса, а затем сложите все эти произведения.
Example
Рассмотрим binary number 1101.11.
Mathematically, мы можем записать это как
(1101.11) 2 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (1 × 2 -1 ) +
(1 × 2 -2 )
⇒ (1101,11) 2 = 8 + 4 + 0 + 1 + 0,5 + 0,25 = 13,75
⇒ (1101,11) 2 = (13,75) 10
Следовательно decimal equivalent двоичного числа 1101,11 равно 13,75.
Двоичное преобразование в восьмеричное
Мы знаем, что основания двоичной и восьмеричной систем счисления равны 2 и 8 соответственно. Три бита двоичного числа эквивалентны одной восьмеричной цифре, поскольку 2 3 = 8.
Выполните эти два шага для преобразования двоичного числа в его эквивалентное восьмеричное число.
Начните с двоичной точки и сделайте группы по 3 бита по обе стороны от двоичной точки. Если при формировании группы из 3-х битов на один или два бита меньше, то необходимо включить необходимое количество нулей на крайних сторонах.
Запишите восьмеричные цифры, соответствующие каждой группе из 3 бит.
Example
Рассмотрим binary number 101110.01101.
Step 1 - Сделайте группы по 3 бита с обеих сторон двоичной точки.
101 110.011 01
Здесь, справа от двоичной точки, последняя группа имеет только 2 бита. Итак, добавьте один ноль на крайнюю сторону, чтобы сделать его группой из 3 бит.
⇒ 101 110.011 010
Step 2 - Запишите восьмеричные цифры, соответствующие каждой группе из 3 бит.
⇒ (101 110,011 010) 2 = (56,32) 8
Следовательно octal equivalent двоичного числа 101110.01101 равно 56.32.
Преобразование двоичного числа в шестнадцатеричное
Мы знаем, что основания двоичной и шестнадцатеричной систем счисления равны 2 и 16 соответственно. Четыре бита двоичного числа эквивалентны одной десятичной шестнадцатеричной цифре, поскольку 2 4 = 16.
Выполните эти два шага для преобразования двоичного числа в его эквивалентное шестнадцатеричное десятичное число.
Начните с двоичной точки и сделайте группы по 4 бита по обе стороны от двоичной точки. Если при образовании группы из 4-х битов несколько бит меньше, то по крайним сторонам нужно добавить необходимое количество нулей.
Запишите шестнадцатеричные цифры, соответствующие каждой группе из 4 бит.
Example
Рассмотрим binary number 101110.01101
Step 1 - Составляйте группы по 4 бита с обеих сторон двоичной точки.
10 1110.0110 1
Здесь первая группа имеет только 2 бита. Итак, добавьте два нуля на крайнюю сторону, чтобы получилась группа из 4 бит. Точно так же добавьте три нуля на крайнюю сторону, чтобы последняя группа также была группой из 4 бит.
⇒ 0010 1110.0110 1000
Step 2 - Запишите шестнадцатеричные десятичные цифры, соответствующие каждой группе из 4 бит.
⇒ (0010 1110.0110 1000) 2 = (2E.68) 16
Следовательно Hexa-decimal equivalent двоичного числа 101110.01101 равно (2E.68).
Преобразование восьмеричного числа в другое основание
Процесс преобразования восьмеричного числа в десятичное отличается от процесса преобразования восьмеричного числа в другие основания. Теперь давайте обсудим преобразование восьмеричного числа в десятичную, двоичную и шестнадцатеричную системы счисления по очереди.
Восьмеричное преобразование в десятичное
Для преобразования восьмеричного числа в его эквивалентное десятичное число сначала умножьте цифры восьмеричного числа на соответствующие позиционные веса, а затем сложите все эти произведения.
Example
Рассмотрим octal number 145.23.
Mathematically, мы можем записать это как
(145,23) 8 = (1 × 8 2 ) + (4 × 8 1 ) + (5 × 8 0 ) + (2 × 8 -1 ) + (3 × 8 -2 )
⇒ (145,23) 8 = 64 + 32 + 5 + 0,25 + 0,05 = 101,3
⇒ (145,23) 8 = (101,3) 10
Следовательно decimal equivalent восьмеричного числа 145,23 равно 101,3.
Восьмеричное преобразование в двоичное
Процесс преобразования восьмеричного числа в эквивалентное двоичное число прямо противоположен процессу преобразования двоичного числа в восьмеричное. Представляя каждую восьмеричную цифру 3 битами, мы получим эквивалентное двоичное число.
Example
Рассмотрим octal number 145.23.
Представьте каждую восьмеричную цифру 3 битами.
(145,23) 8 = (001 100 101,010 011) 2
Значение не меняется при удалении нулей, которые находятся на крайнем крае.
⇒ (145,23) 8 = (1100101.010011) 2
Следовательно binary equivalent восьмеричного числа 145.23 равно 1100101.010011.
Восьмеричное преобразование в шестнадцатеричное
Выполните эти два шага для преобразования восьмеричного числа в его эквивалентное шестнадцатеричное десятичное число.
- Преобразуйте восьмеричное число в его эквивалентное двоичное число.
- Преобразуйте указанное выше двоичное число в его эквивалентное шестнадцатеричное десятичное число.
Example
Рассмотрим octal number 145.23
В предыдущем примере мы получили двоичный эквивалент восьмеричного числа 145,23 как 1100101.010011.
Следуя процедуре преобразования двоичного кода в шестнадцатеричный, мы получим
(1100101.010011) 2 = (65,4 ° C) 16
⇒ (145,23) 8 = (65,4C) 16
Следовательно Hexa-decimal equivalentвосьмеричного числа 145.23 является 65.4 С .
Преобразование шестнадцатеричных чисел в другие основания
Процесс преобразования шестнадцатеричного числа в десятичное отличается от процесса преобразования шестнадцатеричного числа в другое основание. Теперь давайте обсудим преобразование шестнадцатеричного числа в десятичную, двоичную и восьмеричную системы счисления по очереди.
Преобразование шестнадцатеричного числа в десятичное
Для преобразования шестнадцатеричного числа в его эквивалентное десятичное число сначала умножьте цифры шестнадцатеричного числа на соответствующие позиционные веса, а затем сложите все эти произведения.
Example
Рассмотрим Hexa-decimal number 1A5.2
Mathematically, мы можем записать это как
(1A5.2) 16 = (1 × 16 2 ) + (10 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 )
⇒ (1A5.2) 16 = 256 + 160 + 5 + 0,125 = 421,125
⇒ (1A5.2) 16 = (421,125) 10
Следовательно decimal equivalent шестнадцатеричного числа 1A5.2 равно 421,125.
Шестнадцатеричное преобразование в двоичное
Процесс преобразования шестнадцатеричного числа в его эквивалентное двоичное число прямо противоположен процессу преобразования двоичного числа в шестнадцатеричное. Представляя каждую шестнадцатеричную цифру 4 битами, мы получим эквивалентное двоичное число.
Example
Рассмотрим Hexa-decimal number 65.4C
Представьте каждую шестнадцатеричную цифру 4 битами.
(65.4C) 6 = (0110 0101.0100 1100) 2
Значение не меняется при удалении нулей, которые находятся на двух крайних сторонах.
⇒ (65,4C) 16 = (1100101.010011) 2
Следовательно binary equivalent шестнадцатеричного числа 65.4C равно 1100101.010011.
Преобразование шестнадцатеричного числа в восьмеричное
Выполните эти два шага для преобразования шестнадцатеричного числа в его эквивалентное восьмеричное число.
- Преобразуйте десятичное шестнадцатеричное число в его эквивалентное двоичное число.
- Преобразуйте указанное выше двоичное число в его эквивалентное восьмеричное число.
Example
Рассмотрим Hexa-decimal number 65.4C
В предыдущем примере мы получили двоичный эквивалент шестнадцатеричного числа 65.4C как 1100101.010011.
Следуя процедуре преобразования двоичного числа в восьмеричное, мы получим
(1100101.010011) 2 = (145,23) 8
⇒ (65,4C) 16 = (145,23)
Следовательно octal equivalentшестнадцатеричного числа 65,4 C равно 145,23.
Мы можем разделить двоичные числа на следующие две группы: Unsigned numbers и Signed numbers.
Беззнаковые числа
Беззнаковые числа содержат только величину числа. У них нет никаких знаков. Это означает, что все двоичные числа без знака положительны. Как и в десятичной системе счисления, размещение положительного знака перед числом необязательно для представления положительных чисел. Следовательно, все положительные числа, включая ноль, можно рассматривать как числа без знака, если перед числом не установлен положительный знак.
Подписанные номера
Числа со знаком содержат знак и величину числа. Как правило, знак ставится перед числом. Итак, мы должны учитывать положительный знак для положительных чисел и отрицательный знак для отрицательных чисел. Следовательно, все числа можно рассматривать как числа со знаком, если перед числом поставлен соответствующий знак.
Если бит знака равен нулю, это означает, что двоичное число положительно. Аналогично, если бит знака равен единице, это означает, что двоичное число отрицательно.
Представление двоичных чисел без знака
Биты, присутствующие в двоичном числе без знака, содержат magnitudeчисла. Это означает, что если двоичное число без знака содержит‘N’ биты, то все N биты представляют величину числа, поскольку у него нет знакового бита.
Example
Рассмотрим decimal number 108. Двоичный эквивалент этого числа:1101100. Это представление двоичного числа без знака.
(108) 10 = (1101100) 2
Он имеет 7 бит. Эти 7 битов представляют величину числа 108.
Представление двоичных чисел со знаком
Старший значащий бит (MSB) двоичных чисел со знаком используется для обозначения знака чисел. Следовательно, его также называютsign bit. Положительный знак представлен помещением «0» в знаковый бит. Точно так же отрицательный знак представлен помещением «1» в знаковый бит.
Если двоичное число со знаком содержит N битов, тогда (N-1) биты представляют только величину числа, поскольку один бит (MSB) зарезервирован для представления знака числа.
Есть три types of representations для двоичных чисел со знаком
- Форма "Знак-величина"
- Форма дополнения 1
- Форма дополнения 2
Представление положительного числа во всех этих трех формах одинаково. Но в каждой форме будет отличаться только представление отрицательного числа.
Example
Рассмотрим positive decimal number +108. Двоичный эквивалент величины этого числа - 1101100. Эти 7 битов представляют величину числа 108. Поскольку это положительное число, считайте знаковый бит равным нулю, который помещается в крайнюю левую часть величины.
(+108) 10 = (01101100) 2
Следовательно signed binary representationположительного десятичного числа +108. Таким образом, одно и то же представление действительно в форме знак-величина, в форме дополнения до единицы и в форме дополнения до двух для положительного десятичного числа +108.
Форма "Знак-величина"
В форме знака-величины MSB используется для представления sign числа, а остальные биты представляют magnitudeчисла. Итак, просто включите знаковый бит в крайнюю левую часть двоичного числа без знака. Это представление похоже на представление десятичных чисел со знаком.
Example
Рассмотрим negative decimal number -108. Величина этого числа 108. Мы знаем, что двоичное представление 108 без знака - это 1101100. Оно имеет 7 бит. Все эти биты представляют величину.
Поскольку данное число отрицательное, считайте знаковый бит равным единице, который находится в крайней левой части величины.
(-108) 10 = (11101100) 2
Следовательно, знак-величина -108 представляет собой 11101100.
Форма дополнения 1
Дополнение числа до 1 получается следующим образом: complementing all the bitsзнакового двоичного числа. Таким образом, дополнение положительного числа до единицы дает отрицательное число. Точно так же дополнение отрицательного числа до единицы дает положительное число.
Это означает, что если вы выполните два раза дополнение двоичного числа до единицы, включая знаковый бит, то вы получите исходное двоичное число со знаком.
Example
Рассмотрим negative decimal number -108. Величина этого числа 108. Мы знаем, что двоичное представление числа 108 со знаком - 01101100.
Он имеет 8 бит. Старший бит этого числа равен нулю, что указывает на положительное число. Дополнение к нулю равно единице, и наоборот. Итак, заменим нули на единицы, а единицы на нули, чтобы получить отрицательное число.
(-108) 10 = (10010011) 2
Следовательно 1’s complement of (108)10 является (10010011)2.
Форма дополнения 2
Дополнение до 2 двоичного числа получается следующим образом: adding one to the 1’s complementзнакового двоичного числа. Итак, дополнение до 2 положительного числа дает отрицательное число. Точно так же дополнение отрицательного числа до 2 дает положительное число.
Это означает, что если вы выполните двойное дополнение двоичного числа, включая знаковый бит, то вы получите исходное двоичное число со знаком.
Example
Рассмотрим negative decimal number -108.
Мы знаем, что до единицы (108)10 является (10010011)2
Дополнение 2 к (108) 10 = 1 дополнение (108) 10 + 1.
= 10010011 + 1
= 10010100
Следовательно 2’s complement of (108)10 является (10010100)2.
В этой главе давайте обсудим основные арифметические операции, которые могут быть выполнены с любыми двумя двоичными числами со знаком, используя метод дополнения до 2. Вbasic arithmetic operations сложение и вычитание.
Сложение двух двоичных чисел со знаком
Рассмотрим два двоичных числа со знаком A и B, которые представлены в виде дополнения до 2. Мы можем выполнитьadditionэтих двух чисел, что аналогично сложению двух двоичных чисел без знака. Но, если результирующая сумма содержит бит переноса из знака, то отбросьте (игнорируйте) его, чтобы получить правильное значение.
Если результирующая сумма положительна, вы можете определить ее величину напрямую. Но, если результирующая сумма отрицательна, то возьмите ее дополнение до 2, чтобы получить величину.
Пример 1
Давайте выполним addition двух десятичных чисел +7 and +4 используя метод дополнения до 2.
В 2’s complement представления +7 и +4 с 5 битами каждое показаны ниже.
(+7) 10 = (00111) 2
(+4) 10 = (00100) 2
Сложение этих двух чисел есть
(+7) 10 + (+ 4) 10 = (00111) 2 + (00100) 2
⇒ (+7) 10 + (+ 4) 10 = (01011) 2 .
Результирующая сумма содержит 5 бит. Таким образом, нет никакого переноса из знакового бита. Знаковый бит '0' указывает, что результирующая сумма равнаpositive. Итак, величина суммы равна 11 в десятичной системе счисления. Следовательно, сложение двух положительных чисел даст еще одно положительное число.
Пример 2
Давайте выполним addition двух десятичных чисел -7 и -4 используя метод дополнения до 2.
В 2’s complement Представление -7 и -4 с 5 битами каждое показано ниже.
(−7) 10 = (11001) 2
(−4) 10 = (11100) 2
Сложение этих двух чисел есть
(−7) 10 + (−4) 10 = (11001) 2 + (11100) 2
⇒ (−7) 10 + (−4) 10 = (110101) 2 .
Результирующая сумма содержит 6 бит. В этом случае перенос получается из знакового бита. Итак, мы можем удалить это
Итоговая сумма после удаления переноса составляет (−7) 10 + (−4) 10 =(10101)2.
Знаковый бит '1' указывает, что результирующая сумма равна negative. Итак, взяв двойное дополнение к нему, мы получим величину результирующей суммы как 11 в десятичной системе счисления. Следовательно, сложение двух отрицательных чисел даст еще одно отрицательное число.
Вычитание двух двоичных чисел со знаком
Рассмотрим два двоичных числа со знаком A и B, которые представлены в виде дополнения до 2. Мы знаем, что дополнение до 2 положительного числа дает отрицательное число. Итак, всякий раз, когда нам нужно вычесть число B из числа A, возьмите дополнение B до 2 и добавьте его к A. Итак,mathematically мы можем записать это как
A - B = A + (2's complement of B)
Точно так же, если нам нужно вычесть число A из числа B, возьмем дополнение A до 2 и прибавим его к B. Итак, mathematically мы можем записать это как
B - A = B + (2's complement of A)
Итак, вычитание двух двоичных чисел со знаком аналогично сложению двух двоичных чисел со знаком. Но мы должны взять 2-кратное дополнение числа, которое предполагается вычесть. Этоadvantage2-х комплементарной техники. Следуйте тем же правилам сложения двух двоичных чисел со знаком.
Пример 3
Давайте выполним subtraction двух десятичных чисел +7 and +4 используя метод дополнения до 2.
Вычитание этих двух чисел равно
(+7) 10 - (+4) 10 = (+7) 10 + (−4) 10 .
В 2’s complement Представление +7 и -4 с 5 битами каждое показано ниже.
(+7) 10 = (00111) 2
(+4) 10 = (11100) 2
⇒ (+7) 10 + (+4) 10 = (00111) 2 + (11100) 2 = (00011) 2
Здесь перенос, полученный из знакового бита. Итак, мы можем удалить это. Итоговая сумма после удаления переноса равна
(+7) 10 + (+4) 10 =(00011)2
Знаковый бит '0' указывает, что результирующая сумма равна positive. Итак, его величина в десятичной системе счисления равна 3. Следовательно, вычитание двух десятичных чисел +7 и +4 равно +3.
Пример 4
Давайте выполним subtraction of два десятичных числа +4 и +7 используя метод дополнения до 2.
Вычитание этих двух чисел равно
(+4) 10 - (+7) 10 = (+4) 10 + (−7) 10 .
В 2’s complement Представление +4 и -7 с 5 битами каждое показано ниже.
(+4) 10 = (00100) 2
(-7) 10 = (11001) 2
⇒ (+4) 10 + (-7) 10 = (00100) 2 + (11001) 2 = (11101) 2
Здесь перенос не получается из знакового бита. Знаковый бит '1' указывает, что результирующая сумма равнаnegative. Итак, взяв двойное дополнение к нему, мы получим величину итоговой суммы как 3 в десятичной системе счисления. Следовательно, вычитание двух десятичных чисел +4 и +7 равно -3.
При кодировании, когда числа или буквы представлены определенной группой символов, говорят, что это число или буква кодируются. Группа символов называетсяcode. Цифровые данные представляются, хранятся и передаются как группа битов. Эта группа бит также называетсяbinary code.
Двоичные коды можно разделить на два типа.
- Взвешенные коды
- Невзвешенные коды
Если в коде есть позиционные веса, то он называется weighted code. В противном случае это невзвешенный код. Взвешенные коды могут быть дополнительно классифицированы как коды с положительным весом и коды с отрицательным весом.
Двоичные коды для десятичных цифр
В следующей таблице показаны различные двоичные коды десятичных цифр от 0 до 9.
| Десятичная цифра | Код 8421 | Код 2421 | 84-2-1 Код | Код превышения 3 |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0111 | 0100 |
| 2 | 0010 | 0010 | 0110 | 0101 |
| 3 | 0011 | 0011 | 0101 | 0110 |
| 4 | 0100 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1011 | 1000 |
| 6 | 0110 | 1100 | 1010 | 1001 |
| 7 | 0111 | 1101 | 1001 | 1010 |
| 8 | 1000 | 1110 | 1000 | 1011 |
| 9 | 1001 | 1111 | 1111 | 1100 |
У нас есть 10 цифр в десятичной системе счисления. Чтобы представить эти 10 цифр в двоичном формате, нам требуется минимум 4 бита. Но с 4 битами будет 16 уникальных комбинаций нулей и единиц. Поскольку у нас всего 10 десятичных цифр, остальные 6 комбинаций нулей и единиц не требуются.
8 4 2 1 код
Веса этого кода 8, 4, 2 и 1.
В этом коде все положительные веса. Итак, этоpositively weighted code.
Этот код также называется natural BCD (Десятичное число с двоичным кодом) code.
Example
Давайте найдем двоично-десятичный эквивалент десятичного числа 786. Это число состоит из трех десятичных цифр 7, 8 и 6. Из таблицы мы можем записать двоично-десятичные (8421) коды 7, 8 и 6: 0111, 1000 и 0110 соответственно. .
∴ (786)10 = (011110000110)BCD
В представлении BCD 12 бит, поскольку каждый десятичный код BCD имеет 4 бита.
2 4 2 1 код
Веса этого кода - 2, 4, 2 и 1.
В этом коде все положительные веса. Итак, этоpositively weighted code.
Это unnatural BCDкод. Сумма весов неестественных кодов BCD равна 9.
Это self-complementingкод. Самостоятельные коды обеспечивают дополнение до 9 десятичного числа, просто меняя местами 1 и 0 в его эквивалентном представлении 2421.
Example
Давайте найдем 2421 эквивалент десятичного числа 786. Это число состоит из 3 десятичных цифр 7, 8 и 6. Из таблицы мы можем записать коды 2421 из 7, 8 и 6: 1101, 1110 и 1100 соответственно.
Следовательно, 2421 эквивалент десятичного числа 786 равен 110111101100.
8 4-2-1 код
Веса этого кода - 8, 4, -2 и -1.
Этот код имеет отрицательные веса наряду с положительными. Итак, этоnegatively weighted code.
Это unnatural BCD код.
Это self-complementing код.
Example
Давайте найдем эквивалент 8 4-2-1 десятичного числа 786. Это число состоит из 3 десятичных цифр 7, 8 и 6. Из таблицы мы можем записать коды 8 4-2-1 чисел 7, 8 и 6. равны 1001, 1000 и 1010 соответственно.
Следовательно, эквивалент 8 4 -2 -1 десятичного числа 786 равен 100110001010.
Код превышения 3
Этот код не имеет весов. Итак, этоun-weighted code.
Мы получим код Превышения 3 десятичного числа, добавив три (0011) к двоичному эквиваленту этого десятичного числа. Следовательно, он называется кодом превышения 3.
Это self-complementing код.
Example
Давайте найдем эквивалент Превышения 3 десятичного числа 786. Это число состоит из 3 десятичных цифр 7, 8 и 6. Из таблицы мы можем записать коды Превышения 3 из 7, 8 и 6: 1010, 1011 и 1001 соответственно.
Следовательно, эквивалент десятичного числа 786 в избытке 3 равен 101010111001
Код Грея
В следующей таблице показаны 4-битные коды Грея, соответствующие каждому 4-битному двоичному коду.
| Десятичное число | Бинарный код | Код Грея |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
Этот код не имеет весов. Итак, этоun-weighted code.
В приведенной выше таблице последовательные коды Грея различаются только одной битовой позицией. Следовательно, этот код называетсяunit distance код.
Преобразование двоичного кода в код Грея
Выполните следующие действия для преобразования двоичного кода в эквивалентный ему код Грея.
Рассмотрим данный двоичный код и поставим ноль слева от MSB.
Сравните следующие два бита, начиная с нуля. Если 2 бита одинаковы, то выход равен нулю. В противном случае на выходе будет один.
Повторяйте вышеуказанный шаг, пока не получите младший бит кода Грея.
Example
Из таблицы мы знаем, что код Грея, соответствующий двоичному коду 1000, равен 1100. Теперь давайте проверим его, используя описанную выше процедуру.
Учитывая, что двоичный код равен 1000.
Step 1 - Если поставить ноль слева от MSB, двоичный код будет 01000.
Step 2 - Сравнивая два последовательных бита нового двоичного кода, мы получим код Грея как 1100.
Мы знаем, что биты 0 и 1 соответствуют двум разным диапазонам аналоговых напряжений. Таким образом, во время передачи двоичных данных из одной системы в другую также может добавляться шум. Из-за этого могут быть ошибки в полученных данных в другой системе.
Это означает, что бит 0 может измениться на 1 или бит 1 может измениться на 0. Мы не можем избежать помех от шума. Но мы можем сначала вернуть исходные данные, определив наличие каких-либо ошибок, а затем исправив эти ошибки. Для этого мы можем использовать следующие коды.
- Коды обнаружения ошибок
- Коды исправления ошибок
Error detection codes- используются для обнаружения ошибок, присутствующих в полученных данных (битовый поток). Эти коды содержат некоторые биты, которые включаются (добавляются) к исходному потоку битов. Эти коды обнаруживают ошибку, если она возникла при передаче исходных данных (битовый поток).Example - Код четности, код Хэмминга.
Error correction codes- используются для исправления ошибок, присутствующих в полученных данных (битовом потоке), чтобы мы получили исходные данные. Коды исправления ошибок также используют аналогичную стратегию кодов обнаружения ошибок.Example - Код Хэмминга.
Поэтому для обнаружения и исправления ошибок к битам данных во время передачи добавляются дополнительные биты.
Код четности
Легко включить (добавить) один бит четности либо слева от MSB, либо справа от LSB исходного потока битов. Существует два типа кодов четности, а именно код четности и код нечетности, в зависимости от выбранного типа четности.
Код четности
Значение бита четности должно быть равно нулю, если в двоичном коде присутствует четное количество единиц. В противном случае он должен быть одним. Так что, четное количество единиц присутствует вeven parity code. Код четности содержит биты данных и бит четности.
В следующей таблице показаны even parity codesсоответствует каждому 3-битному двоичному коду. Здесь бит четности включен справа от младшего разряда двоичного кода.
| Бинарный код | Бит четности | Код четности |
|---|---|---|
| 000 | 0 | 0000 |
| 001 | 1 | 0011 |
| 010 | 1 | 0101 |
| 011 | 0 | 0110 |
| 100 | 1 | 1001 |
| 101 | 0 | 1010 |
| 110 | 0 | 1100 |
| 111 | 1 | 1111 |
Here, the number of bits present in the even parity codes is 4. So, the possible even number of ones in these even parity codes are 0, 2 & 4.
If the other system receives one of these even parity codes, then there is no error in the received data. The bits other than even parity bit are same as that of binary code.
If the other system receives other than even parity codes, then there will be an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, even parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Odd Parity Code
The value of odd parity bit should be zero, if odd number of ones present in the binary code. Otherwise, it should be one. So that, odd number of ones present in odd parity code. Odd parity code contains the data bits and odd parity bit.
The following table shows the odd parity codes corresponding to each 3-bit binary code. Here, the odd parity bit is included to the right of LSB of binary code.
| Binary Code | Odd Parity bit | Odd Parity Code |
|---|---|---|
| 000 | 1 | 0001 |
| 001 | 0 | 0010 |
| 010 | 0 | 0100 |
| 011 | 1 | 0111 |
| 100 | 0 | 1000 |
| 101 | 1 | 1011 |
| 110 | 1 | 1101 |
| 111 | 0 | 1110 |
Here, the number of bits present in the odd parity codes is 4. So, the possible odd number of ones in these odd parity codes are 1 & 3.
If the other system receives one of these odd parity codes, then there is no error in the received data. The bits other than odd parity bit are same as that of binary code.
If the other system receives other than odd parity codes, then there is an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, odd parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Hamming Code
Hamming code is useful for both detection and correction of error present in the received data. This code uses multiple parity bits and we have to place these parity bits in the positions of powers of 2.
The minimum value of 'k' for which the following relation is correct (valid) is nothing but the required number of parity bits.
$$2^k\geq n+k+1$$
Where,
‘n’ is the number of bits in the binary code (information)
‘k’ is the number of parity bits
Therefore, the number of bits in the Hamming code is equal to n + k.
Let the Hamming code is $b_{n+k}b_{n+k-1}.....b_{3}b_{2}b_{1}$ & parity bits $p_{k}, p_{k-1}, ....p_{1}$. We can place the ‘k’ parity bits in powers of 2 positions only. In remaining bit positions, we can place the ‘n’ bits of binary code.
Based on requirement, we can use either even parity or odd parity while forming a Hamming code. But, the same parity technique should be used in order to find whether any error present in the received data.
Follow this procedure for finding parity bits.
Find the value of p1, based on the number of ones present in bit positions b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of p2, based on the number of ones present in bit positions b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of p3, based on the number of ones present in bit positions b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of parity bits.
Follow this procedure for finding check bits.
Find the value of c1, based on the number of ones present in bit positions b1, b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of c2, based on the number of ones present in bit positions b2, b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of c3, based on the number of ones present in bit positions b4, b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of check bits.
The decimal equivalent of the check bits in the received data gives the value of bit position, where the error is present. Just complement the value present in that bit position. Therefore, we will get the original binary code after removing parity bits.
Example 1
Let us find the Hamming code for binary code, d4d3d2d1 = 1000. Consider even parity bits.
The number of bits in the given binary code is n=4.
We can find the required number of parity bits by using the following mathematical relation.
$$2^k\geq n+k+1$$
Substitute, n=4 in the above mathematical relation.
$$\Rightarrow 2^k\geq 4+k+1$$
$$\Rightarrow 2^k\geq 5+k$$
The minimum value of k that satisfied the above relation is 3. Hence, we require 3 parity bits p1, p2, and p3. Therefore, the number of bits in Hamming code will be 7, since there are 4 bits in binary code and 3 parity bits. We have to place the parity bits and bits of binary code in the Hamming code as shown below.
The 7-bit Hamming code is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}=d_{4}d_{3}d_{2}p_{3}d_{1}p_{2}bp_{1}$
By substituting the bits of binary code, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1} = 100p_{3}Op_{2}p_{1}$. Now, let us find the parity bits.
$$p_{1}=b_{7}\oplus b_{5}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{2}=b_{7}\oplus b_{6}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{3}=b_{7}\oplus b_{6}\oplus b_{5}=1 \oplus 0 \oplus 0=1$$
By substituting these parity bits, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$.
Example 2
In the above example, we got the Hamming code as $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$. Now, let us find the error position when the code received is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001111$.
Now, let us find the check bits.
$$c_{1}=b_{7}\oplus b_{5}\oplus b_{3}\oplus b_{1}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{2}=b_{7}\oplus b_{6}\oplus b_{3}\oplus b_{2}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{3}=b_{7}\oplus b_{6}\oplus b_{5}\oplus b_{4}=1 \oplus 0 \oplus 0 \oplus1 =0$$
The decimal value of check bits gives the position of error in received Hamming code.
$$c_{3}c_{2}c_{1} = \left ( 011 \right )_{2}=\left ( 3 \right )_{10}$$
Therefore, the error present in third bit (b3) of Hamming code. Just complement the value present in that bit and remove parity bits in order to get the original binary code.
Boolean Algebra is an algebra, which deals with binary numbers & binary variables. Hence, it is also called as Binary Algebra or logical Algebra. A mathematician, named George Boole had developed this algebra in 1854. The variables used in this algebra are also called as Boolean variables.
The range of voltages corresponding to Logic ‘High’ is represented with ‘1’ and the range of voltages corresponding to logic ‘Low’ is represented with ‘0’.
Postulates and Basic Laws of Boolean Algebra
In this section, let us discuss about the Boolean postulates and basic laws that are used in Boolean algebra. These are useful in minimizing Boolean functions.
Boolean Postulates
Consider the binary numbers 0 and 1, Boolean variable (x) and its complement (x’). Either the Boolean variable or complement of it is known as literal. The four possible logical OR operations among these literals and binary numbers are shown below.
x + 0 = x
x + 1 = 1
х + х = х
х + х '= 1
Точно так же четыре возможных logical AND операции между этими литералами и двоичными числами показаны ниже.
х.1 = х
х.0 = 0
хх = х
x.x '= 0
Это простые булевы постулаты. Мы можем легко проверить эти постулаты, заменив логическую переменную на «0» или «1».
Note- Дополнение к любой логической переменной равно самой переменной. т.е. (x ')' = x.
Основные законы булевой алгебры
Ниже приведены три основных закона булевой алгебры.
- Коммутативный закон
- Ассоциативный закон
- Распределительное право
Коммутативный закон
Если любая логическая операция с двумя логическими переменными дает один и тот же результат независимо от порядка этих двух переменных, то эта логическая операция называется Commutative. Операции логического ИЛИ и логического И для двух логических переменных x и y показаны ниже.
х + у = у + х
xy = yx
Символ «+» обозначает операцию логического ИЛИ. Точно так же символ '.' обозначает логическую операцию И и необязательно представлять. Коммутативный закон подчиняется операциям логического ИЛИ и логического И.
Ассоциативный закон
Если сначала выполняется логическая операция с любыми двумя логическими переменными, а затем такая же операция с оставшейся переменной дает тот же результат, то эта логическая операция называется Associative. Ниже показаны операции логического ИЛИ и логического И для трех логических переменных x, y и z.
х + (у + г) = (х + у) + г
х. (yz) = (ху) .z
Ассоциативный закон подчиняется операциям логического ИЛИ и логического И.
Распределительное право
Если какая-либо логическая операция может быть распределена на все термины, присутствующие в булевой функции, то эта логическая операция называется Distributive. Распределение операций логического ИЛИ и логического И трех логических переменных x, y и z показано ниже.
х. (у + г) = ху + хz
х + (уz) = (х + у). (х + z)
Распределительный закон подчиняется логическим операциям ИЛИ и логическим операциям И.
Это основные законы булевой алгебры. Мы можем легко проверить эти законы, заменив булевы переменные на «0» или «1».
Теоремы булевой алгебры
Следующие две теоремы используются в булевой алгебре.
- Теорема двойственности
- Теорема ДеМоргана
Теорема двойственности
Эта теорема утверждает, что dualлогической функции получается заменой логического оператора И оператором логического ИЛИ и нулей на единицы. Для каждой логической функции будет соответствующая функция Dual.
Разделим булевы уравнения (отношения), которые мы обсуждали в разделе «Булевы постулаты и основные законы», на две группы. В следующей таблице показаны эти две группы.
| Группа 1 | Группа 2 |
|---|---|
| х + 0 = х | х.1 = х |
| х + 1 = 1 | х.0 = 0 |
| х + х = х | хх = х |
| х + х '= 1 | x.x '= 0 |
| х + у = у + х | xy = yx |
| х + (у + г) = (х + у) + г | х. (yz) = (ху) .z |
| х. (у + г) = ху + хz | х + (уz) = (х + у). (х + z) |
В каждой строке есть два булевых уравнения, двойственных друг другу. Мы можем проверить все эти булевы уравнения Группы 1 и Группы 2, используя теорему двойственности.
Теорема ДеМоргана
Эта теорема полезна при нахождении complement of Boolean function. Он утверждает, что дополнение логического ИЛИ по крайней мере двух логических переменных равно логическому И каждой дополненной переменной.
Теорема ДеМоргана с двумя булевыми переменными x и y может быть представлена как
(х + у) '= х'.у'
Двойственная к вышеуказанной булевой функции есть
(ху) '= х' + у '
Следовательно, дополнение логического И двух логических переменных равно логическому ИЛИ каждой дополняемой переменной. Точно так же мы можем применить теорему ДеМоргана для более чем двух булевых переменных.
Упрощение булевых функций.
До сих пор мы обсуждали постулаты, основные законы и теоремы булевой алгебры. Теперь давайте упростим некоторые булевы функции.
Пример 1
Разрешите нам simplify булева функция, f = p'qr + pq'r + pqr '+ pqr
Мы можем упростить эту функцию двумя способами.
Method 1
Для данной булевой функции f = p'qr + pq'r + pqr '+ pqr.
Step 1- В первом и втором членах r является общим, а в третьем и четвертом членах pq является общим. Итак, возьмите общие термины, используяDistributive law.
⇒ f = (p'q + pq ') r + pq (r' + r).
Step 2- Термины, указанные в первых скобках, могут быть упрощены до операции Ex-OR. Термины, представленные во вторых скобках, можно упростить до «1», используяBoolean postulate
⇒ f = (p ⊕q) r + pq (1)
Step 3- Первый термин не подлежит дальнейшему упрощению. Но второй член можно упростить до pq, используяBoolean postulate.
⇒ f = (p ⊕q) r + pq
Следовательно, упрощенная логическая функция f = (p⊕q)r + pq
Method 2
Для данной булевой функции f = p'qr + pq'r + pqr '+ pqr.
Step 1 - Используйте Boolean postulate, х + х = х. Это означает, что операция логического ИЛИ с любой логической переменной n раз будет равна той же переменной. Итак, мы можем написать последний член pqr еще два раза.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - Использование Distributive lawдля 1- го и 4- го , 2- го и 5- го , 3- го и 6- го триместров.
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r).
Step 3 - Использование Boolean postulate, x + x '= 1 для упрощения терминов, содержащихся в каждой скобке.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - Использование Boolean postulate, x.1 = x для упрощения трех приведенных выше терминов.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Следовательно, упрощенная логическая функция f = pq + qr + pr.
Итак, после упрощения данной логической функции в каждом методе мы получили две разные логические функции. Функционально эти две булевы функции одинаковы. Итак, исходя из требований, мы можем выбрать одну из этих двух логических функций.
Пример 2
Давайте найдем complement булевой функции f = p'q + pq '.
Дополнением к булевой функции является f '= (p'q + pq') '.
Step 1 - Используйте теорему ДеМоргана, (x + y) '= x'.y'.
⇒ f '= (p'q)'. (Pq ')'
Step 2 - Используйте теорему ДеМоргана, (xy) '= x' + y '
⇒ f '= {(p') '+ q'}. {P '+ (q') '}.
Step3 - Используйте булев постулат, (x ')' = x.
⇒ f '= {p + q'}. {P '+ q}.
⇒ f '= pp' + pq + p'q '+ qq'
Step 4 - Используйте булев постулат, xx '= 0.
⇒ f = 0 + pq + p'q '+ 0
⇒ f = pq + p'q '
Следовательно complement булевой функции p'q + pq 'равно pq + p’q’.
Мы получим четыре логических термина продукта, объединив две переменные x и y с помощью логической операции И. Эти логические термины продукта называютсяmin terms или же standard product terms. Минимальные члены - это x'y ', x'y, xy' и xy.
Точно так же мы получим четыре члена логической суммы, объединив две переменные x и y с помощью операции логического ИЛИ. Эти логические суммы называютсяMax terms или же standard sum terms. Термины Max: x + y, x + y ', x' + y и x '+ y'.
В следующей таблице показано представление минимальных и максимальных значений для 2 переменных.
| Икс | y | Минимальные сроки | Максимальные сроки |
|---|---|---|---|
| 0 | 0 | m 0 = x'y ' | М 0 = х + у |
| 0 | 1 | m 1 = x'y | М 1 = х + у ' |
| 1 | 0 | м 2 = ху ' | М 2 = х '+ у |
| 1 | 1 | м 3 = ху | М 3 = х '+ у' |
Если двоичная переменная равна «0», то она представляется как дополнение переменной в минимальном термине и как сама переменная в максимальном термине. Точно так же, если двоичная переменная равна «1», то она представлена как дополнение переменной в Max term и как сама переменная в min term.
Из приведенной выше таблицы мы можем легко заметить, что минимальные и максимальные термины дополняют друг друга. Если имеется n логических переменных, то будет 2 n минимальных и 2 n максимальных терминов.
Канонические формы SoP и PoS
Таблица истинности состоит из набора входов и выходов. Если есть n входных переменных, то будет 2 n возможных комбинаций с нулями и единицами. Таким образом, значение каждой выходной переменной зависит от комбинации входных переменных. Таким образом, каждая выходная переменная будет иметь «1» для некоторой комбинации входных переменных и «0» для некоторой другой комбинации входных переменных.
Следовательно, мы можем выразить каждую выходную переменную двумя способами.
- Каноническая форма SoP
- Каноническая форма PoS
Каноническая форма SoP
Каноническая форма SoP означает форму канонической суммы произведений. В этой форме каждый термин продукта содержит все литералы. Итак, эти условия продукта - не что иное, как минимальные условия. Следовательно, каноническая форма SoP также называетсяsum of min terms форма.
Сначала определите минимальные термины, для которых выходная переменная равна единице, а затем выполните логическое ИЛИ этих минимальных терминов, чтобы получить логическое выражение (функцию), соответствующее этой выходной переменной. Эта логическая функция будет иметь форму суммы минимальных членов.
Выполните ту же процедуру и для других выходных переменных, если существует более одной выходной переменной.
пример
Рассмотрим следующие truth table.
| Входы | Вывод | ||
|---|---|---|---|
| p | q | r | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Здесь выход (f) равен «1» для четырех комбинаций входов. Соответствующие минимальные члены - это p'qr, pq'r, pqr ', pqr. Выполнив логическое ИЛИ для этих четырех минимальных членов, мы получим логическую функцию вывода (f).
Следовательно, логическая функция вывода: f = p'qr + pq'r + pqr '+ pqr. Этоcanonical SoP formвыработки, ф. Мы также можем представить эту функцию в следующих двух обозначениях.
$$f = m_{3}+m_{5}+m_{6}+m_{7}$$
$$f = \sum m\left ( 3,5,6,7 \right )$$
В одном уравнении мы представили функцию как сумму соответствующих минимальных членов. В другом уравнении мы использовали символ для суммирования этих минимальных членов.
Каноническая форма PoS
Каноническая форма PoS означает форму канонического произведения сумм. В этой форме каждый член суммы содержит все литералы. Итак, эти суммы являются не чем иным, как максимальными условиями. Следовательно, каноническая форма PoS также называетсяproduct of Max terms форма.
Сначала определите условия Max, для которых выходная переменная равна нулю, а затем выполните логическое И этих терминов Max, чтобы получить логическое выражение (функцию), соответствующее этой выходной переменной. Эта логическая функция будет представлена в виде произведения максимальных членов.
Выполните ту же процедуру и для других выходных переменных, если существует более одной выходной переменной.
Example
Рассмотрим ту же таблицу истинности из предыдущего примера. Здесь выход (f) равен «0» для четырех комбинаций входов. Соответствующие члены Max: p + q + r, p + q + r ', p + q' + r, p '+ q + r. Выполнив логическое И для этих четырех максимальных членов, мы получим булеву функцию вывода (f).
Следовательно, логическая функция вывода: f = (p + q + r). (P + q + r '). (P + q' + r). (P '+ q + r). Этоcanonical PoS formвыработки, ф. Мы также можем представить эту функцию в следующих двух обозначениях.
$$f=M_{0}.M_{1}.M_{2}.M_{4}$$
$$f=\prod M\left ( 0,1,2,4 \right )$$
В одном уравнении мы представили функцию как произведение соответствующих членов Max. В другом уравнении мы использовали символ для умножения этих максимальных членов.
Булева функция, f = (p + q + r). (P + q + r '). (P + q' + r). (P '+ q + r), является двойником булевой функции, f = p'qr + pq'r + pqr '+ pqr.
Следовательно, и каноническая форма SoP, и каноническая форма PoS являются Dualдруг другу. Функционально эти две формы одинаковы. Исходя из требований, мы можем использовать одну из этих двух форм.
Стандартные формы SoP и PoS
Мы обсудили две канонические формы представления логического вывода (ов). Точно так же есть две стандартные формы представления логического вывода (ов). Это упрощенная версия канонических форм.
- Стандартная форма SoP
- Стандартная форма PoS
Мы обсудим логические вентили в следующих главах. Главныйadvantageстандартных форм состоит в том, что количество входов, применяемых к логическим элементам, может быть минимизировано. Иногда общее количество требуемых логических вентилей сокращается.
Стандартная форма SoP
Стандартная форма SoP означает Standard Sum of Productsформа. В этой форме каждый термин продукта не обязательно должен содержать все литералы. Таким образом, условия продукта могут быть минимальными, а могут и не быть. Следовательно, стандартная форма SoP - это упрощенная форма канонической формы SoP.
Мы получим стандартную форму выходной переменной SoP за два шага.
- Получите каноническую форму выходной переменной SoP
- Упростите приведенную выше логическую функцию, которая находится в канонической форме SoP.
Выполните ту же процедуру и для других выходных переменных, если существует более одной выходной переменной. Иногда невозможно упростить каноническую форму SoP. В этом случае и каноническая, и стандартная форма SoP одинаковы.
Example
Преобразуйте следующую логическую функцию в стандартную форму SoP.
f = p'qr + pq'r + pqr '+ pqr
Данная булева функция находится в канонической форме SoP. Теперь нам нужно упростить эту логическую функцию, чтобы получить стандартную форму SoP.
Step 1 - Используйте Boolean postulate, х + х = х. Это означает, что операция логического ИЛИ с любой логической переменной n раз будет равна той же переменной. Итак, мы можем написать последний член pqr еще два раза.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - Использование Distributive lawдля 1- го и 4- го , 2- го и 5- го , 3- го и 6- го триместров.
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r).
Step 3 - Использование Boolean postulate, x + x '= 1 для упрощения терминов, содержащихся в каждой скобке.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - Использование Boolean postulate, x.1 = x для упрощения вышеуказанных трех членов.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Это упрощенная логическая функция. Следовательноstandard SoP form соответствующая данной канонической форме SoP f = pq + qr + pr
Стандартная форма PoS
Стандартная форма PoS означает Standard Product of Sumsформа. В этой форме каждый член суммы не обязательно должен содержать все литералы. Таким образом, условия суммы могут быть или не быть максимальными условиями. Таким образом, Стандартная форма PoS - это упрощенная форма канонической формы PoS.
Мы получим стандартную форму выходной переменной PoS за два шага.
- Получите каноническую форму выходной переменной PoS
- Упростите приведенную выше логическую функцию, которая находится в канонической форме PoS.
Выполните ту же процедуру и для других выходных переменных, если существует более одной выходной переменной. Иногда невозможно упростить каноническую форму PoS. В этом случае и каноническая, и стандартная форма PoS одинаковы.
Example
Преобразуйте следующую логическую функцию в стандартную форму PoS.
f = (p + q + r). (p + q + r '). (p + q' + r). (p '+ q + r).
Данная логическая функция находится в канонической форме PoS. Теперь нам нужно упростить эту логическую функцию, чтобы получить стандартную форму PoS.
Step 1 - Используйте Boolean postulate, хх = х. Это означает, что операция логического И с любой логической переменной n раз будет равна той же переменной. Итак, мы можем написать первый член p + q + r еще два раза.
⇒ f = (p + q + r). (P + q + r). (P + q + r). (P + q + r '). (P + q' + r). (P '+ q). + г)
Step 2 - Использование Distributive law,x + (yz) = (x + y). (x + z) для 1- й и 4- й скобок, 2- й и 5- й скобок, 3- й и 6- й скобок.
⇒ f = (p + q + rr '). (P + r + qq'). (Q + r + pp ').
Step 3 - Использование Boolean postulate, x.x '= 0 для упрощения терминов, содержащихся в каждой скобке.
⇒ f = (p + q + 0). (P + r + 0). (Q + r + 0).
Step 4 - Использование Boolean postulate, x + 0 = x для упрощения терминов в каждой скобке
⇒ f = (p + q). (P + r). (Q + r).
⇒ f = (p + q). (Q + r). (P + r).
Это упрощенная логическая функция. Следовательноstandard PoS form соответствующая данной канонической форме PoS, является f = (p + q).(q + r).(p + r). Этоdual булевой функции f = pq + qr + pr.
Следовательно, и стандартные формы SoP, и стандартные формы PoS являются двойными друг другу.
В предыдущих главах мы упростили булевы функции, используя булевы постулаты и теоремы. Это трудоемкий процесс, и мы должны переписывать упрощенные выражения после каждого шага.
Чтобы преодолеть эту трудность, Karnaughпредставил метод упрощения булевых функций простым способом. Этот метод известен как метод карты Карно или метод K-карты. Это графический метод, который состоит из 2 n ячеек для n переменных. Соседние ячейки различаются только позицией одного бита.
K-карты для 2-5 переменных
Метод K-Map лучше всего подходит для минимизации булевых функций от 2 переменных до 5 переменных. Теперь давайте обсудим K-Maps для 2–5 переменных по очереди.
2 переменная K-карта
Количество ячеек в К-карте 2 переменных равно четырем, так как количество переменных равно двум. На следующем рисунке показано2 variable K-Map.
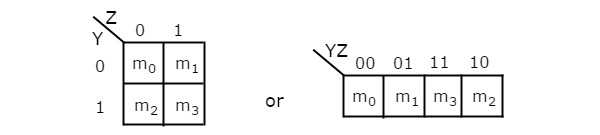
Есть только одна возможность сгруппировать 4 соседних минимальных термина.
Возможные комбинации группировки 2 соседних min термов: {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) и (m 1 , m 3 )}.
3 переменная K-карта
Количество ячеек в К-карте с 3 переменными равно восьми, так как количество переменных равно трем. На следующем рисунке показано3 variable K-Map.
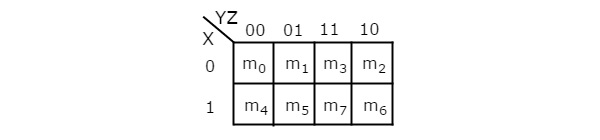
Есть только одна возможность сгруппировать 8 соседних мин. Терминов.
Возможные комбинации группировки 4 соседних min терминов: {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (m 1 , m 3 , m 5 , m 7 ), (m 3 , m 2 , m 7 , m 6 ) и (m 2 , m 0 , m 6 , m 4 )}.
Возможные комбинации группировки 2 соседних min термов: {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 ) , (m 5 , m 7 ), (m 7 , m 6 ), (m 6 , m 4 ), (m 0 , m 4 ), (m 1 , m 5 ), (m 3 , m 7 ) и ( м 2 , м 6 )}.
Если x = 0, то K-карта с 3 переменными становится K-картой с 2 переменными.
4 переменных K-Map
Количество ячеек в K-карте с 4 переменными равно шестнадцати, поскольку количество переменных равно четырем. На следующем рисунке показано4 variable K-Map.
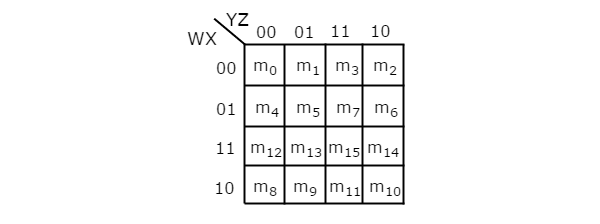
Есть только одна возможность сгруппировать 16 соседних минутных терминов.
Пусть R 1 , R 2 , R 3 и R 4 представляют минимальные члены первой строки, второй строки, третьей строки и четвертой строки соответственно. Точно так же C 1 , C 2 , C 3 и C 4 представляют минимальные члены первого столбца, второго столбца, третьего столбца и четвертого столбца соответственно. Возможные комбинации группировки 8 соседних минимальных терминов: {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 ) , (С 2 , С 3 ), (С 3 , С 4 ), (С 4 , С 1 )}.
Если w = 0, то K-карта с 4 переменными становится K-картой с 3 переменными.
5 переменных K-Map
Количество ячеек в K-карте с 5 переменными равно 32, так как количество переменных равно 5. На следующем рисунке показано 5 variable K-Map.

Есть только одна возможность сгруппировать 32 соседних минимальных термина.
Есть две возможности сгруппировать 16 соседних мин. Терминов. т. е. группировка минимальных терминов от m 0 до m 15 и m 16 до m 31 .
Если v = 0, то K-карта с 5 переменными становится K-картой с 4 переменными.
Во всех вышеупомянутых K-картах мы использовали исключительно обозначение минимальных терминов. Точно так же вы можете использовать исключительно обозначение терминов Max.
Минимизация булевых функций с помощью K-Maps
Если мы рассмотрим комбинацию входов, для которых логическая функция равна '1', то мы получим логическую функцию, которая находится в standard sum of products форма после упрощения K-карты.
Точно так же, если мы рассмотрим комбинацию входов, для которых логическая функция равна '0', мы получим логическую функцию, которая находится в standard product of sums форма после упрощения K-карты.
Следуйте этим rules for simplifying K-maps чтобы получить стандартную форму суммы продуктов.
Выберите соответствующую K-карту на основе количества переменных, присутствующих в булевой функции.
Если логическая функция задана как сумма минимальных терминов, то поместите их в соответствующие ячейки минимальных терминов на K-карте. Если булева функция задана как сумма продуктов, поместите их во все возможные ячейки K-карты, для которых действительны заданные условия продукта.
Проверьте возможности группировки максимального количества соседних. Это должно быть степень двойки. Начните с наибольшей степени двойки и до наименьшей степени двойки. Наивысшая степень равна количеству переменных, рассматриваемых в K-карте, а наименьшая степень равна нулю.
Каждая группа дает буквальный или один термин продукта. Он известен какprime implicant. Главный импликант называетсяessential prime implicant, если хотя бы одна '1' не покрывается никакими другими группами, а покрывается только этой группой.
Запишите все основные импликанты и основные импликанты. Упрощенная логическая функция содержит все основные простые импликанты и только необходимые простые импликанты.
Note 1 - Если выходы не определены для некоторой комбинации входов, то эти выходные значения будут представлены как don’t care symbol ‘x’. Это означает, что мы можем рассматривать их как «0» или «1».
Note 2- Если также присутствуют термины «безразлично», поместите «х» в соответствующие ячейки K-карты. Учитывайте только безразличные 'x', которые помогают сгруппировать максимальное количество соседних. В таких случаях считайте значение безразличия "1".
пример
Разрешите нам simplify следующая логическая функция, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ используя K-карту.
Данная логическая функция находится в форме суммы произведений. Он имеет 4 переменные W, X, Y и Z. Итак, нам требуется4 variable K-map. В4 variable K-map с теми, которые соответствуют данным условиям продукта, показано на следующем рисунке.
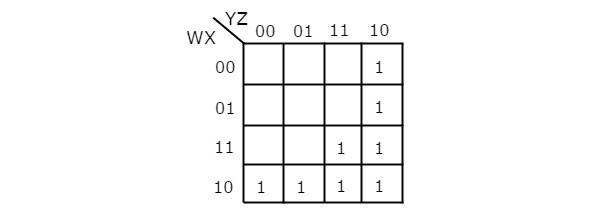
Здесь единицы помещаются в следующие ячейки K-карты.
Ячейки, которые являются общими для пересечения строки 4 и столбцов 1 и 2, соответствуют термину продукта, WX’Y’.
Ячейки, которые являются общими для пересечения строк 3 и 4 и столбцов 3 и 4, соответствуют термину продукта, WY.
Ячейки, которые являются общими для пересечения строк 1 и 2 и столбца 4, соответствуют термину продукта, W’YZ’.
Нет возможности группировать ни 16 соседних, ни 8 соседних. Есть три возможности сгруппировать 4 соседних. После этих трех группировок не остается ни одной разгруппированной. Таким образом, нам не нужно проверять группировку 2-х соседних. В4 variable K-map с этими тремя groupings показано на следующем рисунке.

Здесь мы получили три основных импликанта WX ', WY и YZ'. Все эти основные импликантыessential по следующим причинам.
Два (m8 & m9)группы четвертой строки не попадают ни в какие другие группы. Только четвертая группа строк охватывает эти две строки.
Один (m15)группировки квадратной формы не покрываются никакими другими группировками. Только квадратная группа покрывает это.
Два (m2 & m6)группы четвертого столбца не попадают ни в какие другие группы. Только четвертая группа столбцов охватывает эти две.
Следовательно simplified Boolean function является
f = WX’ + WY + YZ’
Следуйте этим rules for simplifying K-maps для получения стандартного продукта суммовой формы.
Выберите соответствующую K-карту на основе количества переменных, присутствующих в булевой функции.
Если логическая функция задана как произведение максимальной формы термов, тогда поместите нули в соответствующие ячейки максимума термов на K-карте. Если логическая функция задана как произведение суммы сумм, то поместите нули во все возможные ячейки K-карты, для которых действительны заданные члены суммы.
Проверьте возможности группировки максимального количества соседних нулей. Это должно быть степень двойки. Начните с наибольшей степени двойки и до наименьшей степени двойки. Наивысшая степень равна количеству переменных, рассматриваемых в K-карте, а наименьшая степень равна нулю.
Каждая группировка даст буквальный или один суммарный член. Он известен какprime implicant. Главный импликант называетсяessential prime implicant, если хотя бы один '0' не покрывается никакими другими группами, а покрывается только эта группа.
Запишите все основные импликанты и основные импликанты. Упрощенная логическая функция содержит все основные простые импликанты и только необходимые простые импликанты.
Note- Если также присутствуют термины «безразлично», поместите «х» в соответствующие ячейки K-карты. Рассмотрим только безразличный 'x', который помогает сгруппировать максимальное количество соседних нулей. В таких случаях значение безразличия следует рассматривать как «0».
пример
Разрешите нам simplify следующая логическая функция, $f\left ( X,Y,Z \right )=\prod M\left ( 0,1,2,4 \right )$ используя K-карту.
Данная логическая функция является продуктом формы максимума термов. Он имеет 3 переменные X, Y и Z. Итак, нам требуется 3 переменных K-map. Указанные условия Max: M 0 , M 1 , M 2 и M 4 . 3variable K-map с нулями, соответствующими заданным параметрам Max, показано на следующем рисунке.

Нет возможности сгруппировать 8 соседних нулей или 4 соседних нуля. Есть три возможности сгруппировать 2 соседних нуля. После этих трех группировок не остается ни одного нуля в разгруппированном виде. В3 variable K-map с этими тремя groupings показано на следующем рисунке.

Здесь мы получили три простые импликанты X + Y, Y + Z и Z + X. Все эти простые импликанты суть essential потому что один ноль в каждой группе не покрывается никакими другими группами, кроме их индивидуальных группировок.
Следовательно simplified Boolean function является
f = (X + Y).(Y + Z).(Z + X)
Таким образом, мы можем легко упростить логические функции до 5 переменных, используя метод K-map. Для более чем 5 переменных сложно упростить функции с помощью K-Maps. Потому что количествоcells в K-карте получает doubled включив новую переменную.
Из-за этого проверка и группировка соседних единиц (минимальные члены) или соседних нулей (максимальные члены) будут усложнены. Мы обсудимTabular method в следующей главе, чтобы преодолеть трудности метода K-map.
В предыдущей главе мы обсудили метод K-map, который является удобным методом минимизации булевых функций до 5 переменных. Но с помощью этого метода сложно упростить логические функции, имеющие более 5 переменных.
Табличный метод Куайна-Макклюки - это табличный метод, основанный на концепции простых импликантов. Мы знаем этоprime implicant - это член произведения (или суммы), который не может быть дополнительно уменьшен путем объединения с любыми другими членами произведения (или суммы) данной булевой функции.
Этот табличный метод полезен для получения основных импликантов путем многократного использования следующего логического идентификатора.
ху + ху '= х (у + у') = х.1 = х
Процедура табличного метода Куайна-Маккласки
Выполните следующие шаги для упрощения логических функций с использованием табличного метода Куайна-Макклюки.
Step 1 - Упорядочить указанные минимальные сроки в ascending orderи сделайте группы на основе количества единиц, присутствующих в их двоичных представлениях. Итак, будетat most ‘n+1’ groups если есть n логических переменных в булевой функции или n битов в двоичном эквиваленте минимальных условий.
Step 2 - Сравните минимальные термины, представленные в successive groups. Если есть изменение только в одной битовой позиции, тогда возьмите пару этих двух минимальных членов. Поместите этот символ '_' в другую битовую позицию и оставьте оставшиеся биты как есть.
Step 3 - Повторите шаг 2 с вновь сформированными терминами, пока мы не получим все prime implicants.
Step 4 - Сформулируйте prime implicant table. Он состоит из набора строк и столбцов. Простые импликанты можно размещать по строкам, а минимальные термины - по столбцам. Поместите «1» в ячейки, соответствующие минимальным терминам, которые включены в каждый простой импликант.
Step 5- Найдите основные основные импликанты, наблюдая за каждым столбцом. Если минимальный член покрывается только одним простым импликантом, то онessential prime implicant. Эти важные простые импликанты будут частью упрощенной логической функции.
Step 6- Уменьшите таблицу простых импликантов, удалив строку каждого существенного простого импликанта и столбцы, соответствующие минимальным членам, которые покрываются этим существенным простым импликантом. Повторите шаг 5 для уменьшенной простой импликантной таблицы. Остановите этот процесс, когда все минимальные члены данной булевой функции закончились.
пример
Разрешите нам simplify следующая логическая функция, $f\left ( W,X,Y,Z \right )=\sum m\left ( 2,6,8,9,10,11,14,15 \right )$ с использованием табличного метода Куайна-Макклюки.
Данная логическая функция находится в sum of min termsформа. Он имеет 4 переменные W, X, Y и Z. Заданные минимальные члены - это 2, 6, 8, 9, 10, 11, 14 и 15. Порядок возрастания этих минимальных членов основан на количестве единиц, присутствующих в их двоичный эквивалент - 2, 8, 6, 9, 10, 11, 14 и 15. В следующей таблице показаны этиmin terms and their equivalent binary представления.
| Имя группы | Минимальные сроки | W | Икс | Y | Z |
|---|---|---|---|---|---|
| GA1 | 2 | 0 | 0 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | |
| GA2 | 6 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | |
| 10 | 1 | 0 | 1 | 0 | |
| 11 | 1 | 0 | 1 | 1 | |
| 14 | 1 | 1 | 1 | 0 | |
| GA4 | 15 | 1 | 1 | 1 | 1 |
Указанные минимальные термины разбиты на 4 группы в зависимости от количества единиц, присутствующих в их двоичных эквивалентах. В следующей таблице показаны возможныеmerging of min terms из соседних групп.
| Имя группы | Минимальные сроки | W | Икс | Y | Z |
|---|---|---|---|---|---|
| GB1 | 2,6 | 0 | - | 1 | 0 |
| 2,10 | - | 0 | 1 | 0 | |
| 8,9 | 1 | 0 | 0 | - | |
| 8,10 | 1 | 0 | - | 0 | |
| GB2 | 6,14 | - | 1 | 1 | 0 |
| 9,11 | 1 | 0 | - | 1 | |
| 10,11 | 1 | 0 | 1 | - | |
| 10,14 | 1 | - | 1 | 0 | |
| 11,15 | 1 | - | 1 | 1 | |
| 14,15 | 1 | 1 | 1 | - |
Минимальные члены, которые отличаются только одной битовой позицией от соседних групп, объединяются. Этот отличающийся бит представлен этим символом '-'. В этом случае есть три группы, и каждая группа содержит комбинации из двух минимальных терминов. В следующей таблице показаны возможныеmerging of min term pairs из соседних групп.
| Имя группы | Минимальные сроки | W | Икс | Y | Z |
|---|---|---|---|---|---|
| GB1 | 2,6,10,14 | - | - | 1 | 0 |
| 2,10,6,14 | - | - | 1 | 0 | |
| 8,9,10,11 | 1 | 0 | - | - | |
| 8,10,9,11 | 1 | 0 | - | - | |
| GB2 | 10,11,14,15 | 1 | - | 1 | - |
| 10,14,11,15 | 1 | - | 1 | - |
Последовательные группы минимальных пар терминов, которые отличаются только одной битовой позицией, объединяются. Этот отличающийся бит представлен этим символом '-'. В этом случае есть две группы, и каждая группа содержит комбинации из четырех минимальных терминов. Здесь эти комбинации 4-минутных терминов доступны в двух рядах. Итак, мы можем удалить повторяющиеся строки. Уменьшенная таблица после удаления избыточных строк показана ниже.
| Имя группы | Минимальные сроки | W | Икс | Y | Z |
|---|---|---|---|---|---|
| GC1 | 2,6,10,14 | - | - | 1 | 0 |
| 8,9,10,11 | 1 | 0 | - | - | |
| GC2 | 10,11,14,15 | 1 | - | 1 | - |
Дальнейшее объединение комбинаций минимальных термов из соседних групп невозможно, так как они различаются более чем в одной битовой позиции. В приведенной выше таблице есть три строки. Итак, каждая строка дает одну простую импликанту. Следовательноprime implicants являются YZ ', WX' и WY.
В prime implicant table показано ниже.
| Минимальные сроки / основные импликанты | 2 | 6 | 8 | 9 | 10 | 11 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|
| YZ’ | 1 | 1 | 1 | 1 | ||||
| WX’ | 1 | 1 | 1 | 1 | ||||
| WY | 1 | 1 | 1 | 1 |
Первичные импликанты располагаются по строкам, а минимальные термины - по столбцам. Единицы помещаются в общие ячейки простых импликантных строк и соответствующих столбцов с минимальным термином.
Минимальные члены 2 и 6 покрываются только одним простым импликантом YZ’. Итак, этоessential prime implicant. Это будет частью упрощенной логической функции. Теперь удалите эту простую импликантную строку и соответствующие столбцы с минимальным термином. Сокращенная таблица импликантов простых чисел показана ниже.
| Минимальные сроки / основные импликанты | 8 | 9 | 11 | 15 |
|---|---|---|---|---|
| WX’ | 1 | 1 | 1 | |
| WY | 1 | 1 |
Минимальные члены 8 и 9 покрываются только одним простым импликантом WX’. Итак, этоessential prime implicant. Это будет частью упрощенной логической функции. Теперь удалите эту простую импликантную строку и соответствующие столбцы с минимальным термином. Сокращенная таблица импликантов простых чисел показана ниже.
| Минимальные сроки / основные импликанты | 15 |
|---|---|
| WY | 1 |
Минимальный член 15 покрывается только одним простым импликантом WY. Итак, этоessential prime implicant. Это будет частью упрощенной логической функции.
В этом примере задачи у нас есть три основных импликанты, и все они существенны. Следовательноsimplified Boolean function является
f(W,X,Y,Z) = YZ’ + WX’ + WY.
Цифровые электронные схемы работают с напряжениями two logic levelsа именно Logic Low и Logic High. Диапазон напряжений, соответствующий нижнему логическому уровню, представлен «0». Точно так же диапазон напряжений, соответствующий High Logic, представлен цифрой «1».
Базовая цифровая электронная схема, имеющая один или несколько входов и один выход, известна как Logic gate. Следовательно, логические ворота являются строительными блоками любой цифровой системы. Мы можем разделить эти логические ворота на следующие три категории.
- Основные ворота
- Универсальные ворота
- Специальные ворота
Теперь давайте поговорим о логических воротах, подпадающих под каждую категорию один за другим.
Основные ворота
В предыдущих главах мы узнали, что булевы функции могут быть представлены либо в форме суммы произведений, либо в форме произведения сумм в зависимости от требований. Итак, мы можем реализовать эти логические функции с помощью базовых вентилей. Основные ворота - это ворота И, ИЛИ И НЕ.
И ворота
Логический элемент И - это цифровая схема, которая имеет два или более входа и производит выход, который является logical ANDвсех этих входов. Необязательно представлятьLogical AND с символом '.'.
В следующей таблице показаны truth table 2-входного логического элемента И.
| А | B | Y = AB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Здесь A, B - входы, а Y - выход двух входных логических элементов И. Если оба входа равны «1», то только выход Y равен «1». Для остальных комбинаций входов выход Y равен «0».
На следующем рисунке показан symbol логического элемента И, который имеет два входа A, B и один выход Y.

Этот логический элемент И производит выход (Y), который является logical ANDдвух входов A, B. Точно так же, если есть 'n' входов, то логический элемент И создает выход, который является логическим И для всех этих входов. Это означает, что на выходе логического элемента И будет «1», когда на всех входах будет «1».
ИЛИ ворота
Логический элемент ИЛИ - это цифровая схема, которая имеет два или более входов и производит выход, который является логическим ИЛИ всех этих входов. Этотlogical OR обозначается символом «+».
В следующей таблице показаны truth table логического элемента ИЛИ с 2 входами.
| А | B | Y = А + В |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Здесь A, B - входы, а Y - выход двух входных логических элементов ИЛИ. Если оба входа равны «0», то только выход Y равен «0». Для остальных комбинаций входов выход Y равен «1».
На следующем рисунке показан symbol логического элемента ИЛИ, который имеет два входа A, B и один выход Y.

Этот логический элемент ИЛИ производит выход (Y), который является logical ORдвух входов A, B. Точно так же, если есть 'n' входов, то логический элемент ИЛИ производит выход, который является логическим ИЛИ всех этих входов. Это означает, что выход логического элемента ИЛИ будет «1», когда хотя бы один из этих входов равен «1».
НЕ ворота
Логический элемент НЕ - это цифровая схема с одним входом и одним выходом. Выходом НЕ является вентиль.logical inversionввода. Следовательно, вентиль НЕ также называется инвертором.
В следующей таблице показаны truth table НЕ ворота.
| А | Y = A ' |
|---|---|
| 0 | 1 |
| 1 | 0 |
Здесь A и Y - вход и выход логического элемента НЕ соответственно. Если вход A равен «0», то выход Y равен «1». Аналогично, если вход A равен «1», то выход Y равен «0».
На следующем рисунке показан symbol логического элемента НЕ, который имеет один вход A и один выход Y.

Этот вентиль НЕ производит выход (Y), который является complement ввода, A.
Универсальные ворота
Ворота NAND & NOR называются universal gates. Потому что мы можем реализовать любую логическую функцию, которая представляет собой сумму продуктов, используя только вентили NAND. Точно так же мы можем реализовать любую логическую функцию, которая представляет собой произведение сумм, используя только вентили NOR.
Ворота NAND
Логический элемент И-НЕ - это цифровая схема, которая имеет два или более входа и производит выход, который является inversion of logical AND всех этих входов.
В следующей таблице показаны truth table 2-входного логического элемента И-НЕ.
| А | B | Y = (AB) ' |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Здесь A, B - входы, а Y - выход двух входных логических элементов И-НЕ. Когда оба входа равны «1», выход Y равен «0». Если хотя бы один из входных данных равен нулю, тогда выход Y равен «1». Это прямо противоположно операции с двумя входами и вентилем.
The following image shows the symbol of NAND gate, which is having two inputs A, B and one output, Y.
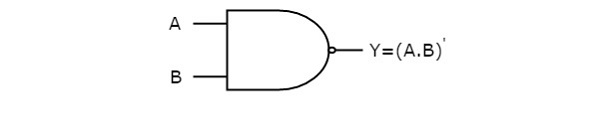
NAND gate operation is same as that of AND gate followed by an inverter. That’s why the NAND gate symbol is represented like that.
NOR gate
NOR gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical OR of all those inputs.
The following table shows the truth table of 2-input NOR gate
| A | B | Y = (A+B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output. If both inputs are ‘0’, then the output, Y is ‘1’. If at least one of the input is ‘1’, then the output, Y is ‘0’. This is just opposite to that of two input OR gate operation.
The following figure shows the symbol of NOR gate, which is having two inputs A, B and one output, Y.

NOR gate operation is same as that of OR gate followed by an inverter. That’s why the NOR gate symbol is represented like that.
Special Gates
Ex-OR & Ex-NOR gates are called as special gates. Because, these two gates are special cases of OR & NOR gates.
Ex-OR gate
The full form of Ex-OR gate is Exclusive-OR gate. Its function is same as that of OR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-OR gate.
| A | B | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input Ex-OR gate. The truth table of Ex-OR gate is same as that of OR gate for first three rows. The only modification is in the fourth row. That means, the output (Y) is zero instead of one, when both the inputs are one, since the inputs having even number of ones.
Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.
Below figure shows the symbol of Ex-OR gate, which is having two inputs A, B and one output, Y.

Ex-OR gate operation is similar to that of OR gate, except for few combination(s) of inputs. That’s why the Ex-OR gate symbol is represented like that. The output of Ex-OR gate is ‘1’, when odd number of ones present at the inputs. Hence, the output of Ex-OR gate is also called as an odd function.
Ex-NOR gate
The full form of Ex-NOR gate is Exclusive-NOR gate. Its function is same as that of NOR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-NOR gate.
| A | B | Y = A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output. The truth table of Ex-NOR gate is same as that of NOR gate for first three rows. The only modification is in the fourth row. That means, the output is one instead of zero, when both the inputs are one.
Therefore, the output of Ex-NOR gate is ‘1’, when both inputs are same. And it is zero, when both the inputs are different.
The following figure shows the symbol of Ex-NOR gate, which is having two inputs A, B and one output, Y.

Ex-NOR gate operation is similar to that of NOR gate, except for few combination(s) of inputs. That’s why the Ex-NOR gate symbol is represented like that. The output of Ex-NOR gate is ‘1’, when even number of ones present at the inputs. Hence, the output of Ex-NOR gate is also called as an even function.
From the above truth tables of Ex-OR & Ex-NOR logic gates, we can easily notice that the Ex-NOR operation is just the logical inversion of Ex-OR operation.
The maximum number of levels that are present between inputs and output is two in two level logic. That means, irrespective of total number of logic gates, the maximum number of Logic gates that are present (cascaded) between any input and output is two in two level logic. Here, the outputs of first level Logic gates are connected as inputs of second level Logic gate(s).
Consider the four Logic gates AND, OR, NAND & NOR. Since, there are 4 Logic gates, we will get 16 possible ways of realizing two level logic. Those are AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-OR, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND, NOR-OR, NOR-NAND, NOR-NOR.
These two level logic realizations can be classified into the following two categories.
- Degenerative form
- Non-degenerative form
Degenerative Form
If the output of two level logic realization can be obtained by using single Logic gate, then it is called as degenerative form. Obviously, the number of inputs of single Logic gate increases. Due to this, the fan-in of Logic gate increases. This is an advantage of degenerative form.
Only 6 combinations of two level logic realizations out of 16 combinations come under degenerative form. Those are AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND.
In this section, let us discuss some realizations. Assume, A, B, C & D are the inputs and Y is the output in each logic realization.
AND-AND Logic
In this logic realization, AND gates are present in both levels. Below figure shows an example for AND-AND logic realization.

We will get the outputs of first level logic gates as $Y_{1}=AB$ and $Y_{2}=CD$
These outputs, $Y_{1}$ and $Y_{2}$ are applied as inputs of AND gate that is present in second level. So, the output of this AND gate is
$$Y=Y_{1}Y_{2}$$
Substitute $Y_{1}$ and $Y_{2}$ values in the above equation.
$$Y=\left ( AB \right )\left ( CD \right )$$
$\Rightarrow Y=ABCD$
Therefore, the output of this AND-AND logic realization is ABCD. This Boolean function can be implemented by using a 4 input AND gate. Hence, it is degenerative form.
AND-NAND Logic
In this logic realization, AND gates are present in first level and NAND gate(s) are present in second level. The following figure shows an example for AND-NAND logic realization.
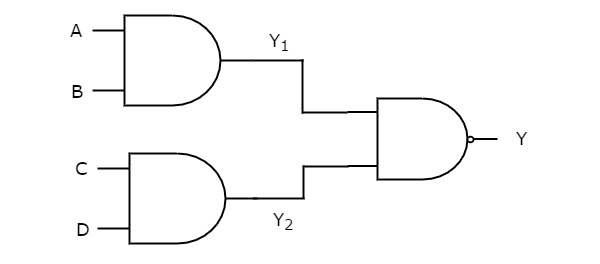
Ранее мы получали выходы логических вентилей первого уровня как $Y_{1} = AB$ и $Y_{2} = CD$
Эти выходы,$Y_{1}$ и $Y_{2}$применяются как входы логического элемента И-НЕ, присутствующего на втором уровне. Итак, выход этого логического элемента И-НЕ
$$Y={\left ( Y_{1}Y_{2} \right )}'$$
Замена $Y_{1}$ и $Y_{2}$ значения в приведенном выше уравнении.
$$Y={\left ( \left ( AB \right ) \left ( CD \right )\right )}'$$
$\Rightarrow Y={\left ( ABCD \right )}'$
Следовательно, выход этой логической реализации И-И-НЕ будет ${\left ( ABCD \right )}'$. Эта логическая функция может быть реализована с помощью логического элемента И-НЕ с 4 входами. Следовательно, этоdegenerative form.
ИЛИ-ИЛИ Логика
В этой логической реализации логические элементы ИЛИ присутствуют на обоих уровнях. На следующем рисунке показан примерOR-OR logic реализация.
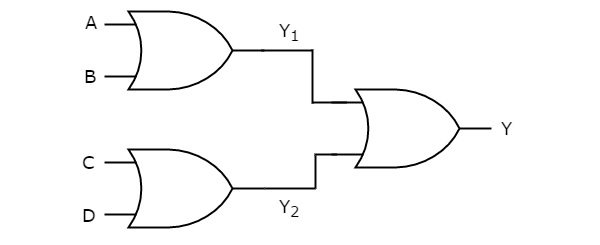
Мы получим выходы логических вентилей первого уровня как $Y_{1}=A+B$ и $Y_{2}=C+D$.
Эти выходы, $Y_{1}$ и $Y_{2}$применяются как входы логического элемента ИЛИ, присутствующего на втором уровне. Итак, выход этого логического элемента ИЛИ
$$Y=Y_{1}+Y_{2}$$
Замена $Y_{1}$ и $Y_{2}$ значения в приведенном выше уравнении.
$$Y=\left ( A+B \right )+\left ( C+D \right )$$
$\Rightarrow Y=A+B+C+D$
Следовательно, выход этой логической реализации ИЛИ-ИЛИ будет A+B+C+D. Эта логическая функция может быть реализована с помощью логического элемента ИЛИ с 4 входами. Следовательно, этоdegenerative form.
Точно так же вы можете проверить, принадлежат ли оставшиеся реализации к этой категории или нет.
Недегенеративная форма
Если выход двухуровневой логической реализации не может быть получен с помощью одного логического элемента, то он называется non-degenerative form.
Остальное 10 combinationsдвухуровневых логических реализаций имеют невырожденную форму. Это AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR.
Теперь давайте обсудим некоторые реализации. Предположим, что A, B, C и D являются входами, а Y - выходом в каждой логической реализации.
И-ИЛИ логика
В этой логической реализации элементы И присутствуют на первом уровне, а элементы ИЛИ - на втором уровне. На рисунке ниже показан примерAND-OR logic реализация.

Ранее мы получали выходы логических вентилей первого уровня как $Y_{1} = AB$ и $Y_{2} = CD$.
Эти выходы Y1 и Y2 применяются как входы логического элемента ИЛИ, который присутствует на втором уровне. Итак, выход этого логического элемента ИЛИ
$$Y=Y_{1}+Y_{2}$$
Замена $Y_{1}$ и $Y_{2}$ значения в приведенном выше уравнении
$$Y=AB+CD$$
Следовательно, выход этой логической реализации И-ИЛИ будет AB+CD. Эта логическая функция находится вSum of Productsформа. Поскольку мы не можем реализовать это с помощью одного логического элемента, эта логическая реализация И-ИЛИ являетсяnon-degenerative form.
Логика И-ИЛИ
В этой логической реализации вентили И присутствуют на первом уровне, а вентили ИЛИ-НЕ присутствуют на втором уровне. На следующем рисунке показан примерAND-NOR logic реализация.

Мы знаем выходы логических вентилей первого уровня как $Y_{1} = AB$ и $Y_{2} = CD$
Эти выходы Y1 и Y2 применяются как входы логического элемента ИЛИ-НЕ, который присутствует на втором уровне. Итак, выход этого логического элемента ИЛИ-НЕ
$$Y={\left ( Y_{1}+Y_{2} \right )}'$$
Замена $Y_{1}$ и $Y_{2}$ значения в приведенном выше уравнении.
$$Y={\left ( AB+CD \right )}'$$
Следовательно, выход этой логической реализации И-ИЛИ: ${\left ( AB+CD \right )}'$. Эта логическая функция находится вAND-OR-Invertформа. Поскольку мы не можем реализовать это с помощью одного логического элемента, эта логическая реализация И-ИЛИ являетсяnon-degenerative form
ИЛИ-И Логика
В этой логической реализации вентили ИЛИ присутствуют на первом уровне, а вентили И - на втором уровне. На следующем рисунке показан примерOR-AND logic реализация.

Ранее мы получали выходы логических вентилей первого уровня как $Y_{1}=A+B$ и $Y_{2}=C+D$.
Эти выходы, $Y_{1}$ и $Y_{2}$применяются как входы логического элемента И, присутствующего на втором уровне. Итак, выход этого логического элемента И равен
$$Y=Y_{1}Y_{2}$$
Замена $Y_{1}$ и $Y_{2}$ значения в приведенном выше уравнении.
$$Y = \left ( A+B \right )\left ( C+D \right )$$
Следовательно, выход этой логической реализации ИЛИ-И будет (A + B) (C + D). Эта логическая функция находится вProduct of Sumsформа. Поскольку мы не можем реализовать это с помощью одного логического элемента, эта логическая реализация ИЛИ-И являетсяnon-degenerative form.
Точно так же вы можете проверить, принадлежат ли оставшиеся реализации к этой категории или нет.
Combinational circuitsсостоят из логических ворот. Эти схемы работают с двоичными значениями. Выход (ы) комбинационной схемы зависит от комбинации имеющихся входов. На следующем рисунке показанblock diagram комбинационной схемы.

Эта комбинационная схема имеет n входных переменных и m выходов. Каждая комбинация входных переменных влияет на выходные данные.
Методика расчета комбинационных схем
Найдите необходимое количество входных переменных и выходов из заданных спецификаций.
Сформулировать Truth table. Если имеется n входных переменных, то будет 2n возможных комбинаций. Найдите выходные значения для каждой комбинации входных данных.
Найди Boolean expressionsдля каждого выхода. При необходимости упростите эти выражения.
Реализуйте приведенные выше логические выражения, соответствующие каждому выходу, используя Logic gates.
Конвертеры кода
Мы обсудили различные коды в главе, названной кодами. Конвертеры, преобразующие один код в другой, называютсяcode converters. Эти преобразователи кода в основном состоят из логических вентилей.
пример
Конвертер двоичного кода в код Грея
Давайте реализуем преобразователь, который преобразует 4-битный двоичный код WXYZ в его эквивалентный код Грея ABCD.
В следующей таблице показаны Truth table преобразователя 4-битного двоичного кода в код Грея.
| Двоичный код WXYZ | WXYZ Код серого ABCD |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 |
| 1001 | 1101 |
| 1010 | 1111 |
| 1011 | 1110 |
| 1100 | 1010 |
| 1101 | 1011 |
| 1110 | 1001 |
| 1111 | 1000 |
Из таблицы истинности мы можем написать Boolean functions для каждого выходного бита кода Грея, как показано ниже.
$$A=\sum m\left (8,9,10,11,12,13,14,15 \right )$$
$$B=\sum m\left (4,5,6,7,8,9,10,11 \right )$$
$$C=\sum m\left (2,3,4,5,10,11,12,13 \right )$$
$$D=\sum m\left (1,2,5,6,9,10,13,14 \right )$$
Давайте упростим вышеуказанные функции, используя 4 переменных K-Maps.
На следующем рисунке показан 4 variable K-Map для упрощения Boolean function, A.

Сгруппировав 8 смежных, мы получили $A=W$.
На следующем рисунке показан 4 variable K-Map для упрощения Boolean function, B.

Есть две группы по 4 смежных. После группировки мы получим B как
$$B={W}'X+W{X}'=W\oplus X $$
Точно так же после упрощения мы получим следующие логические функции для C и D.
$$C={X}'Y+X{Y}'=X \oplus Y$$
$$D={Y}'Z+Y{Z}'=Y \oplus Z$$
На следующем рисунке показан circuit diagram 4-битного двоичного кода в преобразователь кода Грея.

Поскольку выходы зависят только от текущих входов, этот преобразователь 4-битного двоичного кода в код Грея представляет собой комбинационную схему. Точно так же вы можете реализовать другие конвертеры кода.
Генератор битов четности
Существует два типа генераторов бит четности в зависимости от типа генерируемого бита четности. Even parity generatorгенерирует бит четности. Так же,odd parity generator генерирует бит нечетной четности.
Генератор четности
Теперь давайте реализуем генератор четности для 3-битного двоичного входа, WXY. Он генерирует бит четности P. Если на входе присутствует нечетное количество единиц, то бит четности P должен быть равен «1», чтобы результирующее слово содержало четное количество единиц. Для других комбинаций ввода, бит четности, P должен быть «0». В следующей таблице показаныTruth table генератора четности.
| Двоичный вход WXY | Бит четности P |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
Из приведенной выше таблицы истинности мы можем написать Boolean function для бита четности как
$$P={W}'{X}'Y+{W}'X{Y}'+W{X}'{Y}'+WXY$$
$\Rightarrow P={W}'\left ( {X}'Y+X{Y}' \right )+W\left ({X}'{Y}'+XY \right )$
$\Rightarrow P={W}'\left ( X \oplus Y \right )+W{\left (X \oplus Y \right )}'=W \oplus X \oplus Y$
На следующем рисунке показан circuit diagram генератора четности.

Эта схема состоит из двух Exclusive-OR gatesпо два входа каждый. Первый вентиль Исключающее ИЛИ, имеющий два входа W и X, дает выход W X. Этот выход задается как один вход второго элемента Исключающее ИЛИ. Другой вход этого второго логического элемента «Исключающее ИЛИ» - Y и дает на выходе W ⊕ X ⊕ Y.
Генератор нечетной четности
Если на входе присутствует четное количество единиц, то бит нечетной четности P должен быть равен «1», чтобы результирующее слово содержало нечетное количество единиц. Для других комбинаций ввода, бит нечетной четности, P должен быть «0».
Выполните ту же процедуру, что и генератор четной четности, для реализации генератора нечетной четности. Вcircuit diagram генератора нечетной четности показан на следующем рисунке.

Приведенная выше принципиальная схема состоит из логического элемента Ex-OR на первом уровне и элемента Ex-NOR на втором уровне. Поскольку нечетная четность прямо противоположна четной, мы можем разместить инвертор на выходе генератора четной четности. В этом случае первый и второй уровни содержат логический элемент ExOR на каждом уровне, а третий уровень состоит из инвертора.
Проверка четности
Существует два типа средств проверки четности в зависимости от типа проверки четности. Even parity checkerпроверяет ошибки в переданных данных, которые содержат биты сообщения вместе с четностью. Так же,odd parity checker проверяет ошибки в переданных данных, которые содержат биты сообщения вместе с нечетной четностью.
Проверка четности
Теперь давайте реализуем схему проверки четности. Предположим, что это 3-битный двоичный вход, WXY передается вместе с битом четности P. Итак, результирующее слово (данные) содержит 4 бита, которые будут приняты как входные данные средства проверки четности.
Это порождает even parity check bit, E. Этот бит будет равен нулю, если полученные данные содержат четное количество единиц. Это означает, что в полученных данных нет ошибки. Этот бит проверки четности будет равен единице, если полученные данные содержат нечетное количество единиц. Это означает, что в полученных данных есть ошибка.
В следующей таблице показаны Truth table проверки четности.
| 4-битные полученные данные WXYP | Бит проверки четности E |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 1 |
| 0011 | 0 |
| 0100 | 1 |
| 0101 | 0 |
| 0110 | 0 |
| 0111 | 1 |
| 1000 | 1 |
| 1001 | 0 |
| 1010 | 0 |
| 1011 | 1 |
| 1100 | 0 |
| 1101 | 1 |
| 1110 | 1 |
| 1111 | 0 |
Из приведенной выше таблицы истинности мы можем заметить, что значение бита проверки четности равно «1», когда в полученных данных присутствует нечетное количество единиц. Это означает, что логическая функция бита проверки четности являетсяodd function. Функция исключающее ИЛИ удовлетворяет этому условию. Следовательно, мы можем напрямую написатьBoolean function бит проверки четности как
$$E=W \oplus X \oplus Y \oplus P$$
На следующем рисунке показан circuit diagram проверки четности.

Эта схема состоит из трех Exclusive-OR gatesпо два входа каждый. Ворота первого уровня производят выходы$W \oplus X$ & $Y \oplus P$. Схема исключающего ИЛИ, находящаяся на втором уровне, дает на выходе$W \oplus X \oplus Y \oplus P$
Проверка нечетной четности
Предположим, 3-битный двоичный вход, WXY передается вместе с битом нечетной четности P. Итак, результирующее слово (данные) содержит 4 бита, которые будут приняты как входные данные средства проверки нечетности.
Это порождает odd parity check bit, E. Этот бит будет равен нулю, если полученные данные содержат нечетное количество единиц. Это означает, что в полученных данных нет ошибки. Этот бит проверки нечетности будет равен единице, если полученные данные содержат четное количество единиц. Это означает, что в полученных данных есть ошибка.
Выполните ту же процедуру, что и для проверки четности, для реализации проверки на нечетность. Вcircuit diagram средства проверки нечетной четности показано на следующем рисунке.

Приведенная выше принципиальная схема состоит из ворот Ex-OR на первом уровне и ворот Ex-NOR на втором уровне. Поскольку нечетная четность прямо противоположна четной, мы можем разместить инвертор на выходе проверки четности. В этом случае первый, второй и третий уровни содержат два логических элемента Ex-OR, один вентиль Ex-OR и один инвертор соответственно.
Двоичный сумматор
Самая простая арифметическая операция - сложение. Схема, которая выполняет сложение двух двоичных чисел, известна какBinary adder. Во-первых, давайте реализуем сумматор, который выполняет сложение двух битов.
Половина сумматора
Полусумматор - это комбинационная схема, которая выполняет сложение двух двоичных чисел A и B из single bit. Он выдает сумму двух выходов, S & carry, C.
В Truth table Полусумматор показан ниже.
| Входы | Выходы | ||
|---|---|---|---|
| А | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Когда мы складываем два бита, результирующая сумма может иметь десятичные значения от 0 до 2. Мы можем представить десятичные цифры 0 и 1 с помощью одного бита в двоичном формате. Но мы не можем представить десятичную цифру 2 одним битом в двоичном формате. Итак, нам нужны два бита для его представления в двоичном формате.
Пусть сумма, S - младший бит и перенос, C - самый старший бит результирующей суммы. Для первых трех комбинаций входов, перенос, C равен нулю, а значение S будет равно нулю или единице в зависимости отnumber of onesприсутствует на входах. Но для последней комбинации входов, перенос, C равен единице, а сумма, S равна нулю, поскольку результирующая сумма равна двум.
Из таблицы истинности мы можем напрямую записать Boolean functions для каждого выхода как
$$S=A \oplus B$$
$C=AB$
Вышеупомянутые функции можно реализовать с помощью логического элемента Ex-OR с 2 входами и логического элемента AND с 2 входами. Вcircuit diagram Полусумматор показан на следующем рисунке.

В приведенной выше схеме два входных элемента Ex-OR и два входа AND создают сумму, S и перенос C соответственно. Следовательно, полусумматор выполняет сложение двух битов.
Полный сумматор
Полный сумматор - комбинационная схема, выполняющая addition of three bitsA, B и C дюйм . Где A и B - два параллельных значащих бита, а C in - бит переноса, который генерируется на предыдущем этапе. Этот полный сумматор также производит два выхода суммы, S & carry, C out , которые аналогичны половинному сумматору.
В Truth table Полный сумматор показан ниже.
| Входы | Выходы | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Когда мы складываем три бита, итоговая сумма может иметь десятичные значения от 0 до 3. Мы можем представить десятичные цифры 0 и 1 с помощью одного бита в двоичном формате. Но мы не можем представить десятичные цифры 2 и 3 одним битом в двоичном формате. Итак, нам нужны два бита для представления этих двух десятичных цифр в двоичном формате.
Пусть сумма, S - младший бит и перенос, C out - самый старший бит результирующей суммы. Значения выходов для всех комбинаций входов в таблице истинности легко заполнить. Просто посчитайтеnumber of onesприсутствовать на входах и записывать эквивалентное двоичное число на выходах. Если C in равно нулю, то таблица истинности полного сумматора такая же, как таблица истинности полусумматора.
Мы получим следующее Boolean functions для каждого выхода после упрощения.
$$S=A \oplus B \oplus C_{in}$$
$c_{out} = AB + \left ( A \oplus B \right )c_{in}$
Сумма S равна единице, когда на входах присутствует нечетное количество единиц. Мы знаем, что вентиль Ex-OR производит вывод, что является нечетной функцией. Итак, мы можем использовать либо два логических элемента Ex-OR с 2 входами, либо один вентиль Ex-OR с 3 входами, чтобы получить сумму S. Мы можем реализовать перенос C , используя два логических элемента AND с 2 входами и один вентиль OR. Вcircuit diagram Полный сумматор показан на следующем рисунке.
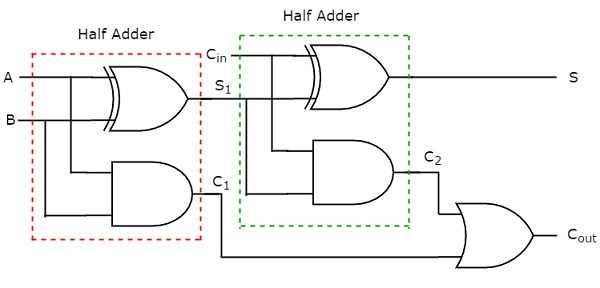
Этот сумматор называется Full adderпотому что для реализации одного полного сумматора нам требуются два полусумматора и один вентиль ИЛИ. Если C in равно нулю, тогда полный сумматор становится половинным сумматором. В этом легко убедиться по приведенной выше принципиальной схеме или по булевым функциям выходов полного сумматора.
4-битный двоичный сумматор
4-битный двоичный сумматор выполняет addition of two 4-bit numbers. Пусть 4-битные двоичные числа,$A=A_{3}A_{2}A_{1}A_{0}$ и $B= B_{3}B_{2}B_{1}B_{0}$. Мы можем реализовать 4-битный двоичный сумматор одним из двух следующих способов.
Используйте один полусумматор для добавления двух младших разрядов и три полных сумматора для добавления трех старших значащих битов.
Для единообразия используйте четыре полных сумматора. Поскольку начальный перенос C in равен нулю, полный сумматор, который используется для добавления младших битов, становится полусумматором.
Пока мы рассматривали второй подход. Вblock diagram 4-битного двоичного сумматора показан на следующем рисунке.

Здесь 4 полных сумматора соединены каскадом. Каждый полный сумматор получает соответствующие биты двух параллельных входов A и B. Выход переноса одного полного сумматора будет входом переноса последующего полного сумматора более высокого порядка. Этот 4-битный двоичный сумматор дает результирующую сумму, содержащую не более 5 бит. Итак, выполнением последнего этапа Полный сумматор будет MSB.
Таким образом, мы можем реализовать любой двоичный сумматор более высокого порядка, просто каскадируя необходимое количество полных сумматоров. Этот двоичный сумматор также называютripple carry (binary) adder потому что перенос распространяется (колеблется) от одного этапа к следующему.
Бинарный вычитатель
Схема, которая выполняет вычитание двух двоичных чисел, известна как Binary subtractor. Мы можем реализовать двоичный вычитатель следующими двумя способами.
- Каскад Полные вычитатели
- 2 метод дополнения
В первом методе мы получим n-битный двоичный вычитатель путем каскадирования n полных вычитателей. Итак, сначала вы можете реализовать половинный вычитатель и полный вычитатель, аналогичные половинному сумматору и полному сумматору. Затем вы можете реализовать n-битный двоичный вычитатель путем каскадирования n полных вычитателей. Итак, у нас будут две отдельные схемы для двоичного сложения и вычитания двух двоичных чисел.
Во втором методе мы можем использовать тот же двоичный сумматор для вычитания двух двоичных чисел, просто внося некоторые изменения во второй ввод. Таким образом, выполняется внутренняя операция двоичного сложения, но на выходе получается вычитание.
Мы знаем, что вычитание двух двоичных чисел A и B может быть записано как,
$$A-B = A+\left ( {2}'s \: compliment \: of \: B \right )$$
$\Rightarrow A-B = A+\left ( {1}'s \: compliment \: of \: B \right )+1$
4-битный двоичный вычитатель
4-битный двоичный вычитатель дает subtraction of two 4-bit numbers. Пусть 4-битные двоичные числа,$A=A_{3}A_{2}A_{1}A_{0}$ и $B= B_{3}B_{2}B_{1}B_{0}$. Внутренне работа 4-битного двоичного вычитателя аналогична работе 4-битного двоичного сумматора. Если обычные биты двоичного числа A, дополненные биты двоичного числа B и начальный перенос (заимствование), C in как один применяются к 4-битному двоичному сумматору, то он становится 4-битным двоичным вычитателем. Вblock diagram 4-битного двоичного вычитателя показано на следующем рисунке.

Этот 4-битный двоичный вычитатель дает на выходе не более 5 битов. Если двоичное число A больше двоичного числа B, то старший бит вывода равен нулю, а оставшиеся биты содержат величину AB. Если двоичное число A меньше двоичного числа B, то старший бит вывода равен единице. Итак, возьмите два дополнения вывода, чтобы получить величину AB.
Таким образом, мы можем реализовать любой двоичный вычитатель более высокого порядка, просто каскадируя необходимое количество полных сумматоров с необходимыми изменениями.
Двоичный сумматор / вычитатель
Схема, которую можно использовать для сложения или вычитания двух двоичных чисел в любое время, известна как Binary Adder / subtractor. И двоичный сумматор, и двоичный вычитатель содержат набор полных сумматоров, которые каскадированы. Входные биты двоичного числа A напрямую применяются как в двоичном сумматоре, так и в двоичном вычитателе.
Есть два различия во входах полных сумматоров, которые присутствуют в двоичном сумматоре и двоичном вычитателе.
Входные биты двоичного числа B напрямую применяются к полным сумматорам в двоичном сумматоре, тогда как дополненные биты двоичного числа B применяются к полным сумматорам в двоичном вычитателе.
Начальный перенос C 0 = 0 применяется в 4-битном двоичном сумматоре, тогда как начальный перенос (заимствование) C 0 = 1 применяется в 4-битном двоичном вычитателе.
Мы знаем, что 2-input Ex-OR gateпроизводит вывод, который совпадает с выводом первого ввода, когда другой ввод равен нулю. Точно так же он производит вывод, который является дополнением первого ввода, когда другой ввод является одним.
Следовательно, мы можем применить входные биты двоичного числа B к логическим элементам Ex-OR с 2 входами. Другой вход для всех этих вентилей Ex-OR - C 0 . Таким образом, на основе значения C 0 вентили Ex-OR производят либо нормальные, либо дополненные биты двоичного числа B.
4-битный двоичный сумматор / вычитатель
4-битный двоичный сумматор / вычитатель производит сложение или вычитание двух 4-битных чисел на основе значения начального переноса или заимствования, 0 . Пусть 4-битные двоичные числа,$A=A_{3}A_{2}A_{1}A_{0}$ и $B= B_{3}B_{2}B_{1}B_{0}$. Работа 4-битного двоичного сумматора / вычитателя аналогична работе 4-битного двоичного сумматора и 4-битного двоичного вычитателя.
Примените обычные биты двоичных чисел A и B и начальный перенос или заимствование C 0 извне к 4-битному двоичному сумматору. Вblock diagram 4-битного двоичного сумматора / вычитателя показан на следующем рисунке.
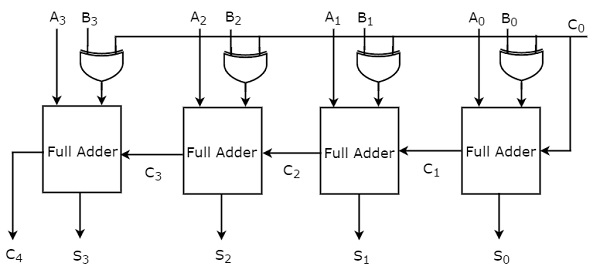
Если начальный перенос 0 равен нулю, то каждый полный сумматор получает нормальные биты двоичных чисел A и B. Таким образом, 4-битный двоичный сумматор / вычитатель производит выходной сигнал, который являетсяaddition of two binary numbers А и Б.
Если начальное заимствование, 0 равно единице, то каждый полный сумматор получает нормальные биты двоичного числа A и дополненные биты двоичного числа B. Итак, 4-битный двоичный сумматор / вычитатель выдает результат, который являетсяsubtraction of two binary numbers А и Б.
Следовательно, с помощью дополнительных вентилей Ex-OR одна и та же схема может использоваться как для сложения, так и для вычитания двух двоичных чисел.
Decoderпредставляет собой комбинационную схему, которая имеет n входных линий и максимум 2 n выходных линий. Когда декодер включен, один из этих выходов будет активным высоким в зависимости от комбинации присутствующих входов. Это означает, что декодер обнаруживает определенный код. Выходы декодера не что иное, какmin terms входных переменных 'n' (строк), когда он включен.
2-4 декодера
Пусть декодер с 2 по 4 имеет два входа A 1 и A 0 и четыре выхода Y 3 , Y 2 , Y 1 и Y 0 . Вblock diagram 2-4 декодера показан на следующем рисунке.

Один из этих четырех выходов будет иметь значение «1» для каждой комбинации входов при включении, E - «1». ВTruth table 2-4 декодера показаны ниже.
| включить | Входы | Выходы | ||||
|---|---|---|---|---|---|---|
| E | A1 | A0 | Y3 | Y2 | Y1 | Y0 |
| 0 | Икс | Икс | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Из таблицы истинности мы можем написать Boolean functions для каждого выхода как
$$Y_{3}=E.A_{1}.A_{0}$$
$$ Y_{2}=E.A_{1}.{A_{0}}'$$
$$ Y_{1}=E.{A_{1}}'.A_{0}$$
$$ Y_{0}=E.{A_{1}}'.{A_{0}}'$$
Каждый выход имеет один термин продукта. Итак, всего существует четыре термина продукта. Мы можем реализовать эти четыре условия продукта, используя четыре логических элемента И, каждый из которых имеет по три входа и два инвертора. Вcircuit diagram 2-4 декодера показан на следующем рисунке.

Следовательно, выходы 2-4 декодера - это не что иное, как min termsдвух входных переменных A 1 и A 0 , при включении E равно единице. Если включено, E равно нулю, то все выходы декодера будут равны нулю.
Точно так же декодер с 3 по 8 производит восемь минутных членов трех входных переменных A 2 , A 1 и A 0, а декодер с 4 по 16 производит шестнадцать минутных членов четырех входных переменных A 3 , A 2 , A 1 и A 0 .
Реализация декодеров высшего порядка
Теперь давайте реализуем следующие два декодера более высокого порядка, используя декодеры более низкого порядка.
- От 3 до 8 декодеров
- Декодер от 4 до 16
От 3 до 8 декодеров
В этом разделе давайте реализуем 3 to 8 decoder using 2 to 4 decoders. Мы знаем, что декодер с 2 по 4 имеет два входа, A 1 и A 0, и четыре выхода, от Y 3 до Y 0 . Принимая во внимание, что декодер от 3 до 8 имеет три входа A 2 , A 1 и A 0 и восемь выходов от Y 7 до Y 0 .
Мы можем найти количество декодеров низшего порядка, необходимое для реализации декодера более высокого порядка, используя следующую формулу.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
Где,
$m_{1}$ - количество выходов декодера низшего порядка.
$m_{2}$ - количество выходов декодера более высокого порядка.
Вот, $m_{1}$ = 4 и $m_{2}$ = 8. Подставьте эти два значения в формулу выше.
$$Required \: number \: of \: 2 \: to \: 4 \: decoders=\frac{8}{4}=2$$
Следовательно, для реализации одного декодера от 3 до 8 нам требуется от двух до четырех декодеров. Вblock diagram От 3 до 8 декодеров с использованием от 2 до 4 декодеров показано на следующем рисунке.

Параллельные входы A 1 и A 0 применяются к каждому 2–4 декодеру. Дополнение входа A 2 подключается к Enable, E нижнего декодера 2-4, чтобы получить выходы Y 3 до Y 0 . Этиlower four min terms. Вход A 2 напрямую подключен к Enable, E верхнего декодера 2–4, чтобы получить выходы от Y 7 до Y 4 . Этиhigher four min terms.
Декодер от 4 до 16
В этом разделе давайте реализуем 4 to 16 decoder using 3 to 8 decoders. Мы знаем, что декодер от 3 до 8 имеет три входа A 2 , A 1 и A 0 и восемь выходов от Y 7 до Y 0 . Принимая во внимание, что декодер с 4 по 16 имеет четыре входа A 3 , A 2 , A 1 и A 0 и шестнадцать выходов, от Y 15 до Y 0.
Нам известна следующая формула для определения количества требуемых декодеров более низкого порядка.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
Замена, $m_{1}$ = 8 и $m_{2}$ = 16 в приведенной выше формуле.
$$Required \: number \: of \: 3 \: to \: 8 decoders=\frac{16}{8}=2$$
Следовательно, для реализации одного декодера от 4 до 16 нам потребуется два декодера от 3 до 8. Вblock diagram От 4 до 16 декодеров с использованием от 3 до 8 декодеров показано на следующем рисунке.

Параллельные входы A 2 , A 1 и A 0 применяются к каждому декодеру от 3 до 8. Дополнение к входу A3 подключается к Enable, E нижнего декодера с 3 по 8, чтобы получить выходы от Y 7 до Y 0 . Этиlower eight min terms. Вход A 3 напрямую подключен к Enable, E верхнего декодера с 3 по 8 для получения выходов от Y 15 до Y 8 . Этиhigher eight min terms.
An Encoder- комбинационная схема, выполняющая операцию, обратную декодеру. Он имеет максимум 2 n входных и n выходных линий. Он сгенерирует двоичный код, эквивалентный входу, который является активным High. Следовательно, кодер кодирует 2 n входных строк n битами. Необязательно представлять разрешающий сигнал в энкодерах.
Кодировщик с 4 на 2
Пусть с 4 по 2 Энкодер имеет четыре входа Y 3 , Y 2 , Y 1 и Y 0 и два выхода A 1 и A 0 . Вblock diagram от 4 до 2 Энкодер показан на следующем рисунке.

В любой момент только один из этих 4 входов может иметь значение «1», чтобы на выходе получить соответствующий двоичный код. ВTruth table энкодера от 4 до 2 показан ниже.
| Входы | Выходы | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Из таблицы истинности мы можем написать Boolean functions для каждого выхода как
$$A_{1}=Y_{3}+Y_{2}$$
$$A_{0}=Y_{3}+Y_{1}$$
Мы можем реализовать две вышеупомянутые логические функции, используя два входа ИЛИ. Вcircuit diagram энкодера с 4 по 2 показано на следующем рисунке.

Приведенная выше принципиальная схема содержит два логических элемента ИЛИ. Эти логические элементы ИЛИ кодируют четыре входа двумя битами.
Восьмеричный в двоичный кодировщик
Восьмерично-двоичный энкодер имеет восемь входов от Y 7 до Y 0 и три выхода A 2 , A 1 и A 0 . Восьмерично-двоичный кодировщик - это не что иное, как кодировщик 8 к 3. Вblock diagram преобразование восьмеричного в двоичный кодировщик показано на следующем рисунке.
В любой момент только один из этих восьми входов может иметь значение «1», чтобы получить соответствующий двоичный код. ВTruth table от восьмеричного до двоичного кодировщика показано ниже.
| Входы | Выходы | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Из таблицы истинности мы можем написать Boolean functions для каждого выхода как
$$A_{2}=Y_{7}+Y_{6}+Y_{5}+Y_{4}$$
$$A_{1}=Y_{7}+Y_{6}+Y_{3}+Y_{2}$$
$$A_{0}=Y_{7}+Y_{5}+Y_{3}+Y_{1}$$
Мы можем реализовать вышеуказанные логические функции, используя четыре входных логических элемента ИЛИ. Вcircuit diagram преобразование восьмеричного в двоичный кодировщик показано на следующем рисунке.

Приведенная выше принципиальная схема содержит три логических элемента ИЛИ с 4 входами. Эти логические элементы ИЛИ кодируют восемь входов тремя битами.
Недостатки энкодера
Ниже приведены недостатки обычного кодировщика.
Возникает неоднозначность, когда все выходы энкодера равны нулю. Потому что это может быть код, соответствующий входам, когда только наименее значимый вход равен единице или когда все входы равны нулю.
Если более чем один вход активен High, кодировщик выдает выходной сигнал, который может быть неправильным кодом. Заexample, если и Y 3, и Y 6 равны «1», то кодировщик выдает 111 на выходе. Это не эквивалентный код, соответствующий Y 3 , когда он равен «1», ни эквивалентный код, соответствующий Y 6 , когда он равен «1».
Итак, чтобы преодолеть эти трудности, мы должны назначить приоритеты каждому входу кодировщика. Тогда выходом энкодера будет (двоичный) код, соответствующий активному высокому входу (ам), который имеет более высокий приоритет. Этот кодировщик называетсяpriority encoder.
Приоритетный кодировщик
Энкодер с приоритетом от 4 до 2 имеет четыре входа Y 3 , Y 2 , Y 1 и Y 0 и два выхода A 1 и A 0 . Здесь вход Y 3 имеет наивысший приоритет, тогда как вход Y 0 имеет самый низкий приоритет. В этом случае, даже если несколько входов имеют значение «1» одновременно, выходом будет (двоичный) код, соответствующий входу, который имеетhigher priority.
Мы рассмотрели еще один output, V чтобы знать, действителен ли код, доступный на выходах, или нет.
Если хотя бы один вход энкодера равен «1», то код, доступный на выходах, является действительным. В этом случае выход V будет равен 1.
Если все входы энкодера равны «0», то код, доступный на выходах, недействителен. В этом случае выход V будет равен 0.
В Truth table кодировщика с приоритетом от 4 до 2 показан ниже.
| Входы | Выходы | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | Икс | 0 | 1 | 1 |
| 0 | 1 | Икс | Икс | 1 | 0 | 1 |
| 1 | Икс | Икс | Икс | 1 | 1 | 1 |
Использовать 4 variable K-maps для получения упрощенных выражений для каждого вывода.
Упрощенный Boolean functions находятся
$$A_{1}=Y_{3}+Y_{2}$$
$A_{0}=Y_{3}+{Y_{2}}'Y_{1}$
Аналогичным образом мы получим логическую функцию вывода V как
$$V=Y_{3}+Y_{2}+Y_{1}+Y_{0}$$
Мы можем реализовать вышеупомянутые логические функции с помощью логических вентилей. Вcircuit diagram энкодер с приоритетом от 4 до 2 показан на следующем рисунке.

Приведенная выше принципиальная схема содержит два логических элемента ИЛИ с 2 входами, один логический элемент ИЛИ с 4 входами, один логический элемент И с двумя входами и инвертор. Здесь комбинация логического элемента И и инвертора используется для создания действительного кода на выходах, даже если несколько входов одновременно равны «1». Следовательно, эта схема кодирует четыре входа двумя битами на основеpriority назначается каждому входу.
Multiplexerпредставляет собой комбинационную схему, которая имеет максимум 2 n входов данных, n строк выбора и одну строку вывода. Один из этих входов данных будет связан с выходом на основе значений строк выбора.
Поскольку имеется n строк выбора, будет 2 n возможных комбинаций нулей и единиц. Таким образом, каждая комбинация будет выбирать только один ввод данных. Мультиплексор еще называютMux.
Мультиплексор 4x1
Мультиплексор 4x1 имеет четыре входа данных I 3 , I 2 , I 1 и I 0 , две строки выбора s 1 и s 0 и один выход Y.block diagram мультиплексора 4x1 показано на следующем рисунке.

Один из этих 4 входов будет подключен к выходу на основе комбинации входов, присутствующих в этих двух строках выбора. Truth table мультиплексора 4x1 показан ниже.
| Линии выбора | Вывод | |
|---|---|---|
| S1 | S0 | Y |
| 0 | 0 | Я 0 |
| 0 | 1 | Я 1 |
| 1 | 0 | Я 2 |
| 1 | 1 | Я 3 |
Из таблицы истинности мы можем напрямую записать Boolean function для вывода Y как
$$Y={S_{1}}'{S_{0}}'I_{0}+{S_{1}}'S_{0}I_{1}+S_{1}{S_{0}}'I_{2}+S_{1}S_{0}I_{3}$$
Мы можем реализовать эту логическую функцию с помощью инверторов, логических элементов И и ИЛИ. Вcircuit diagram мультиплексора 4x1 показан на следующем рисунке.

Мы легко можем понять работу указанной схемы. Точно так же вы можете реализовать мультиплексор 8x1 и мультиплексор 16x1, выполнив ту же процедуру.
Реализация мультиплексоров высшего порядка.
Теперь давайте реализуем следующие два мультиплексора более высокого порядка, используя мультиплексоры более низкого порядка.
- Мультиплексор 8x1
- Мультиплексор 16x1
Мультиплексор 8x1
В этом разделе давайте реализуем мультиплексор 8x1, используя мультиплексоры 4x1 и мультиплексор 2x1. Мы знаем, что мультиплексор 4x1 имеет 4 входа данных, 2 строки выбора и один выход. Принимая во внимание, что мультиплексор 8x1 имеет 8 входов данных, 3 строки выбора и один выход.
Итак, нам потребуется два 4x1 Multiplexersна первом этапе, чтобы получить 8 входов данных. Поскольку каждый мультиплексор 4x1 производит один выходной сигнал, нам требуется2x1 Multiplexer на втором этапе, рассматривая выходы первого этапа как входы и производя окончательный результат.
Пусть мультиплексор 8x1 имеет восемь входов данных с I 7 по I 0 , три строки выбора s 2 , s 1 и s0 и один выход Y.Truth table мультиплексора 8x1 показан ниже.
| Выбор входов | Вывод | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | Я 0 |
| 0 | 0 | 1 | Я 1 |
| 0 | 1 | 0 | Я 2 |
| 0 | 1 | 1 | Я 3 |
| 1 | 0 | 0 | Я 4 |
| 1 | 0 | 1 | Я 5 |
| 1 | 1 | 0 | Я 6 |
| 1 | 1 | 1 | Я 7 |
Мы можем легко реализовать мультиплексор 8x1, используя мультиплексоры более низкого порядка, с учетом приведенной выше таблицы истинности. Вblock diagram мультиплексора 8x1 показан на следующем рисунке.

Такой же selection lines, s1 & s0применяются к обоим мультиплексорам 4x1. Входы данных верхнего мультиплексора 4x1 - это I 7 - I 4, а входы данных нижнего мультиплексора 4x1 - I 3 - I 0 . Следовательно, каждый мультиплексор 4x1 производит вывод на основе значений строк выбора s 1 и s 0 .
Выходы мультиплексоров 4x1 первой ступени используются как входы мультиплексора 2x1, присутствующего во второй ступени. Другойselection line, s2 применяется к мультиплексору 2x1.
Если s 2 равно нулю, то выход мультиплексора 2x1 будет одним из 4 входов с I 3 по I 0 на основе значений строк выбора s 1 и s 0 .
Если s 2 равно единице, то выход мультиплексора 2x1 будет одним из 4 входов с I 7 по I 4 на основе значений строк выбора s 1 и s 0 .
Следовательно, общая комбинация двух мультиплексоров 4x1 и одного мультиплексора 2x1 работает как один мультиплексор 8x1.
Мультиплексор 16x1
В этом разделе давайте реализуем мультиплексор 16x1, используя мультиплексоры 8x1 и мультиплексор 2x1. Мы знаем, что мультиплексор 8x1 имеет 8 входов данных, 3 строки выбора и один выход. В то время как мультиплексор 16x1 имеет 16 входов данных, 4 строки выбора и один выход.
Итак, нам потребуется два 8x1 Multiplexersна первом этапе, чтобы получить 16 входных данных. Поскольку каждый мультиплексор 8x1 производит один выход, нам требуется мультиплексор 2x1 на втором этапе, рассматривая выходы первого этапа как входные и для получения окончательного вывода.
Пусть мультиплексор 16x1 имеет шестнадцать входов данных с I 15 по I 0 , четыре строки выбора с s 3 по s 0 и один выход Y.Truth table мультиплексора 16x1 показан ниже.
| Выбор входов | Вывод | |||
|---|---|---|---|---|
| S3 | S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 0 | Я 0 |
| 0 | 0 | 0 | 1 | Я 1 |
| 0 | 0 | 1 | 0 | Я 2 |
| 0 | 0 | 1 | 1 | Я 3 |
| 0 | 1 | 0 | 0 | Я 4 |
| 0 | 1 | 0 | 1 | Я 5 |
| 0 | 1 | 1 | 0 | Я 6 |
| 0 | 1 | 1 | 1 | Я 7 |
| 1 | 0 | 0 | 0 | Я 8 |
| 1 | 0 | 0 | 1 | Я 9 |
| 1 | 0 | 1 | 0 | Я 10 |
| 1 | 0 | 1 | 1 | Я 11 |
| 1 | 1 | 0 | 0 | Я 12 |
| 1 | 1 | 0 | 1 | Я 13 |
| 1 | 1 | 1 | 0 | Я 14 |
| 1 | 1 | 1 | 1 | Я 15 |
Мы можем легко реализовать мультиплексор 16x1, используя мультиплексоры более низкого порядка, с учетом приведенной выше таблицы истинности. Вblock diagram мультиплексора 16x1 показано на следующем рисунке.

В same selection lines, s2, s1 & s0применяются к обоим мультиплексорам 8x1. Входы данных верхнего мультиплексора 8x1 - от I 15 до I 8, а входы данных нижнего мультиплексора 8x1 - от I 7 до I 0 . Следовательно, каждый мультиплексор 8x1 производит вывод на основе значений строк выбора, s 2 , s 1 и s 0 .
Выходы мультиплексора 8x1 первой ступени используются как входы мультиплексора 2x1, который присутствует во второй ступени. Другойselection line, s3 применяется к мультиплексору 2x1.
Если s 3 равно нулю, то выход мультиплексора 2x1 будет одним из 8 входов Is 7 до I 0 на основе значений строк выбора s 2 , s 1 и s 0 .
Если s 3 равен единице, то выход мультиплексора 2x1 будет одним из 8 входов с I 15 по I 8 на основе значений строк выбора s 2 , s 1 и s 0 .
Следовательно, общая комбинация двух мультиплексоров 8x1 и одного мультиплексора 2x1 работает как один мультиплексор 16x1.
De-Multiplexerпредставляет собой комбинационную схему, которая выполняет операцию, обратную мультиплексору. Он имеет один вход, n строк выбора и максимум 2 n выходов. Вход будет подключен к одному из этих выходов в зависимости от значений строк выбора.
Поскольку имеется n строк выбора, будет 2 n возможных комбинаций нулей и единиц. Таким образом, каждая комбинация может выбрать только один выход. Демультиплексор также называютDe-Mux.
Демультиплексор 1x4
Демультиплексор 1x4 имеет один вход I, две строки выбора, s 1 и s 0, и четыре выхода Y 3 , Y 2 , Y 1 и Y 0 . Вblock diagram Демультиплексора 1x4 показано на следующем рисунке.

Единственный вход «I» будет подключен к одному из четырех выходов, от Y 3 до Y 0, на основе значений строк выбора s 1 и s0. ВTruth table Демультиплексора 1x4 показан ниже.
| Выбор входов | Выходы | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
Из приведенной выше таблицы истинности мы можем напрямую написать Boolean functions для каждого выхода как
$$Y_{3}=s_{1}s_{0}I$$
$$Y_{2}=s_{1}{s_{0}}'I$$
$$Y_{1}={s_{1}}'s_{0}I$$
$$Y_{0}={s_1}'{s_{0}}'I$$
Мы можем реализовать эти логические функции, используя инверторы и логические элементы И с 3 входами. Вcircuit diagram Демультиплексора 1x4 показано на следующем рисунке.

Мы легко можем понять работу указанной схемы. Точно так же вы можете реализовать демультиплексор 1x8 и демультиплексор 1x16, выполнив ту же процедуру.
Реализация демультиплексоров высшего порядка
Теперь давайте реализуем следующие два де-мультиплексора более высокого порядка, используя де-мультиплексоры более низкого порядка.
- Демультиплексор 1x8
- Демультиплексор 1x16
Демультиплексор 1x8
В этом разделе давайте реализуем демультиплексор 1x8, используя демультиплексоры 1x4 и демультиплексор 1x2. Мы знаем, что де-мультиплексор 1x4 имеет один вход, две линии выбора и четыре выхода. Принимая во внимание, что De-Multiplexer 1x8 имеет один вход, три линии выбора и восемь выходов.
Итак, нам потребуется два 1x4 De-Multiplexersна втором этапе, чтобы получить окончательные восемь результатов. Поскольку количество входов на втором этапе равно двум, нам потребуется1x2 DeMultiplexerна первом этапе, так что выходы первого этапа будут входами второго этапа. Вход этого демультиплексора 1x2 будет общим входом демультиплексора 1x8.
Пусть у демультиплексора 1x8 есть один вход I, три строки выбора s 2 , s 1 и s 0 и выходы от Y 7 до Y 0 . ВTruth table Демультиплексора 1x8 показан ниже.
| Выбор входов | Выходы | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Мы можем легко реализовать демультиплексор 1x8, используя мультиплексоры более низкого порядка, учитывая приведенную выше таблицу истинности. Вblock diagram Демультиплексора 1x8 показан на следующем рисунке.

Общее selection lines, s1 & s0применяются к обоим де-мультиплексорам 1x4. Выходы верхнего демультиплексора 1x4 - от Y 7 до Y 4, а выходы нижнего демультиплексора 1x4 - от Y 3 до Y 0 .
Другой selection line, s2применяется к демультиплексору 1x2. Если s 2 равно нулю, то один из четырех выходов нижнего демультиплексора 1x4 будет равен входу I на основе значений строк выбора s 1 и s 0 . Аналогично, если s 2 равно единице, то один из четырех выходов верхнего демультиплексора 1x4 будет равен входу I на основе значений строк выбора s 1 и s 0 .
Демультиплексор 1x16
В этом разделе давайте реализуем демультиплексор 1x16, используя демультиплексоры 1x8 и демультиплексор 1x2. Мы знаем, что De-Multiplexer 1x8 имеет один вход, три линии выбора и восемь выходов. В то же время, 1x16 De-Multiplexer имеет один вход, четыре линии выбора и шестнадцать выходов.
Итак, нам потребуется два 1x8 De-Multiplexersна втором этапе, чтобы получить окончательные шестнадцать выходов. Поскольку количество входов на втором этапе равно двум, нам потребуется1x2 DeMultiplexerна первом этапе, так что выходы первого этапа будут входами второго этапа. Вход этого демультиплексора 1x2 будет общим входом демультиплексора 1x16.
Пусть у де-мультиплексора 1x16 есть один вход I, четыре строки выбора s 3 , s 2 , s 1 и s 0 и выходы от Y 15 до Y 0 . Вblock diagram Демультиплексора 1x16 с использованием мультиплексоров более низкого порядка показан на следующем рисунке.
Общее selection lines s2, s1 & s0применяются к обоим де-мультиплексорам 1x8. Выходы верхнего демультиплексора 1x8 - от Y 15 до Y 8, а выходы нижнего демультиплексора 1x8 - от Y 7 до Y 0 .
Другой selection line, s3применяется к демультиплексору 1x2. Если s 3 равно нулю, то один из восьми выходов нижнего демультиплексора 1x8 будет равен входу I на основе значений строк выбора s 2 , s 1 и s 0 . Аналогично, если s3 равно единице, то один из 8 выходов верхнего де-мультиплексора 1x8 будет равен входу I на основе значений строк выбора s 2 , s 1 и s 0 .
Программируемые логические устройства (PLDs)интегральные схемы. Они содержат массив элементов И и еще один массив элементов ИЛИ. Существует три типа PLD в зависимости от типа массива (ов), который имеет программируемую функцию.
- Программируемая постоянная память
- Программируемая логика массива
- Программируемый логический массив
Процесс ввода информации в эти устройства известен как programming. По сути, пользователи могут программировать эти устройства или ИС электрически, чтобы реализовать логические функции в зависимости от требований. Здесь термин «программирование» относится к программированию оборудования, но не к программированию программного обеспечения.
Программируемая постоянная память (PROM)
Постоянное запоминающее устройство (ПЗУ) - это запоминающее устройство, в котором постоянно хранится двоичная информация. Это означает, что мы не сможем изменить эту сохраненную информацию позже. Если ПЗУ имеет программируемую функцию, то оно называетсяProgrammable ROM (PROM). Пользователь может один раз запрограммировать двоичную информацию электрически с помощью программатора PROM.
PROM - это программируемое логическое устройство, которое имеет фиксированный массив И и программируемый массив ИЛИ. Вblock diagram ППЗУ показан на следующем рисунке.

Здесь входы логических элементов И не являются программируемыми. Итак, мы должны сгенерировать 2 n условий продукта, используя 2 n логических элементов И, каждый из которых имеет n входов. Мы можем реализовать эти условия продукта с помощью декодера nx2 n . Итак, этот декодер генерирует 'n'min terms.
Здесь программируются входы логических элементов ИЛИ. Это означает, что мы можем запрограммировать любое количество требуемых условий продукта, поскольку все выходы логических элементов И применяются как входы для каждого элемента ИЛИ. Следовательно, выходы PROM будут в видеsum of min terms.
пример
Реализуем следующие Boolean functions с помощью PROM.
$$A(X,Y,Z)=\sum m\left ( 5,6,7 \right )$$
$$B(X,Y,Z)=\sum m\left ( 3,5,6,7 \right )$$
Указанные две функции представлены в виде суммы минимальных термов, и каждая функция имеет три переменных X, Y и Z. Итак, нам требуется от 3 до 8 декодеров и два программируемых логических элемента ИЛИ для создания этих двух функций. СоответствующиеPROM показано на следующем рисунке.

Здесь декодер от 3 до 8 генерирует восемь минутных термов. Два программируемых логических элемента ИЛИ имеют доступ ко всем этим минимальным условиям. Но программируются только необходимые минимальные члены, чтобы каждый вентиль ИЛИ производил соответствующие булевы функции. Символ «X» используется для программируемых соединений.
Программируемая матричная логика (PAL)
PAL - это программируемое логическое устройство, которое имеет программируемый массив И и фиксированный массив ИЛИ. Преимущество PAL состоит в том, что мы можем генерировать только требуемые термины продукта логической функции вместо генерации всех минимальных членов с помощью программируемых логических элементов И. Вblock diagram PAL показан на следующем рисунке.

Здесь вводы логических элементов И являются программируемыми. Это означает, что каждый вентиль И имеет как нормальные, так и дополненные входы переменных. Итак, исходя из требований, мы можем запрограммировать любой из этих входов. Итак, мы можем сгенерировать только необходимыеproduct terms используя эти ворота AND.
Здесь входы логических элементов ИЛИ не являются программируемыми. Таким образом, количество входов в каждый вентиль ИЛИ будет фиксированного типа. Следовательно, примените эти необходимые условия продукта к каждому вентилю ИЛИ в качестве входных данных. Следовательно, выходы PAL будут в видеsum of products form.
пример
Реализуем следующие Boolean functions используя PAL.
$$A=XY+X{Z}'$$
$$A=X{Y}'+Y{Z}'$$
Данные две функции выражаются в форме суммы продуктов. В каждой булевой функции присутствуют два термина продукта. Итак, нам требуются четыре программируемых логических элемента И и два фиксированных логических элемента ИЛИ для выполнения этих двух функций. СоответствующиеPAL показано на следующем рисунке.

В programmable AND gatesимеют доступ как к нормальным, так и к дополненным входам переменных. На приведенном выше рисунке входы X,${X}'$, Y, ${Y}'$, Z & ${Z}'$, доступны на входах каждого логического элемента И. Итак, запрограммируйте только необходимые литералы, чтобы сгенерировать один член продукта для каждого логического элемента AND. Символ «X» используется для программируемых соединений.
Здесь входы логических элементов ИЛИ имеют фиксированный тип. Итак, необходимые условия продукта подключены ко входам каждогоOR gate. Таким образом, элементы ИЛИ производят соответствующие логические функции. Символ '.' используется для фиксированных подключений.
Программируемый логический массив (PLA)
PLA - это программируемое логическое устройство, которое имеет как программируемый массив И, так и массив программируемого ИЛИ. Следовательно, это наиболее гибкий PLD. Вblock diagram PLA показан на следующем рисунке.

Здесь вводы логических элементов И являются программируемыми. Это означает, что каждый вентиль И имеет как нормальные, так и дополненные входы переменных. Итак, исходя из требований, мы можем запрограммировать любой из этих входов. Итак, мы можем сгенерировать только необходимыеproduct terms используя эти ворота AND.
Здесь также программируются входы логических элементов ИЛИ. Таким образом, мы можем запрограммировать любое количество требуемых условий продукта, поскольку все выходы логических элементов И применяются как входы для каждого элемента ИЛИ. Следовательно, выходы PAL будут в видеsum of products form.
пример
Реализуем следующие Boolean functions с помощью PLA.
$$A=XY+X{Z}'$$
$$B=X{Y}'+YZ+X{Z}'$$
Данные две функции выражаются в форме суммы продуктов. Количество членов произведения, присутствующих в данных булевых функциях A и B, равно двум и трем соответственно. Один термин продукта,${Z}'X$ является общим для каждой функции.
Итак, нам требуются четыре программируемых логических элемента И и два программируемых логических элемента ИЛИ для выполнения этих двух функций. СоответствующиеPLA показано на следующем рисунке.
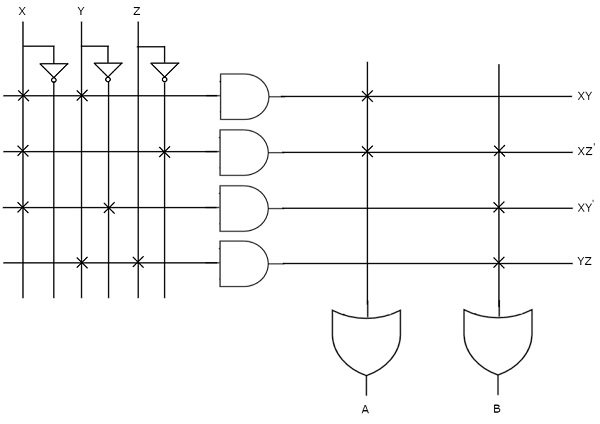
В programmable AND gatesимеют доступ как к нормальным, так и к дополненным входам переменных. На приведенном выше рисунке входы X,${X}'$, Y, ${Y}'$, Z & ${Z}'$, доступны на входах каждого логического элемента И. Итак, запрограммируйте только необходимые литералы, чтобы сгенерировать один член продукта для каждого логического элемента AND.
Все эти условия продукта доступны на входах каждого programmable OR gate. Но запрограммируйте только необходимые термины продукта для создания соответствующих логических функций каждым логическим элементом ИЛИ. Символ «X» используется для программируемых соединений.
В предыдущих главах мы реализовали различные комбинационные схемы с использованием логических вентилей. За исключением элемента НЕ, остальные все логические элементы имеют как минимум два входа и один выход. Точно так жеthreshold gate также содержит как минимум один вход и только один выход.
Кроме того, он содержит соответствующие веса для каждого входа и пороговое значение. Значения этих весов и порога могут иметь любое конечное действительное число.
Основы порогового гейта
Пусть входы порогового элемента - X 1 , X 2 , X 3 ,…, X n . Соответствующие веса этих входов: W 1 , W 2 , W 3 ,…, W n . Вsymbol Порогового затвора показано на следующем рисунке.
Threshold gateпредставлен в виде круга и имеет n входов от X 1 до X n и единственный выход Y. Этот круг состоит из двух частей. Одна часть представляет веса, соответствующие входам, а другая часть представляет пороговое значение T.
Сумма произведений входов с соответствующими весами известна как weighted sum. Если эта взвешенная сумма больше или равна пороговому значению T, то только выход Y будет равен единице. В противном случае выход Y будет равен нулю.
Mathematically, мы можем записать это отношение между входами и выходом порогового вентиля, как показано ниже.
$$Y=1, if \: \: W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}+...W_{n}X_{n}\geq T$$
= 0 в противном случае.
Следовательно, мы можем реализовать различные логические элементы и булевы функции, просто изменяя значения весов и / или порогового значения T.
пример
Давайте найдем simplified Boolean function для следующих пороговых ворот.

Этот пороговый вентиль имеет три входа X 1 , X 2 , X 3 и один выход Y.
Веса, соответствующие входам X 1 , X 2 и X 3, равны W 1 = 2, W 2 = 1 и W 3 = -4 соответственно.
Значение порогового строба T = -1.
В weighted sum порога ворот
$$W=W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}$$
Подставьте указанные веса в приведенное выше уравнение.
$$\Rightarrow W=2X_{1}+X_{2}-4X_{3}$$
Выходной сигнал порогового элемента Y будет равен «1», если W ≥ −1, в противном случае он будет равен «0».
Следующее table показывает взаимосвязь между входом и выходом для всех возможных комбинаций входов.
| Входы | Взвешенная сумма | Вывод | ||
|---|---|---|---|---|
| $X_{1}$ | $X_{2}$ | $X_{3}$ | $W=2X_{1}+X_{2}-4X_{3}$ | $Y$ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
Из приведенной выше таблицы мы можем написать Boolean function для вывода Y как
$$Y= \sum m\left ( 0,2,4,6,7 \right )$$
Упрощение этой логической функции с использованием 3 variable K-Map показано на следующем рисунке.

Следовательно simplified Boolean function для данного порогового строба $Y={X_{3}'}+X_{1}X_{2}$.
Синтез пороговых функций.
Пороговый вентиль также называют universal gateпотому что мы можем реализовать любую логическую функцию с помощью пороговых вентилей. Иногда может оказаться невозможным реализовать несколько логических вентилей и логических функций с помощью одного порогового вентиля. В этом случае нам может потребоваться несколько пороговых ворот.
Следуйте этим steps для реализации логической функции с использованием одного порогового вентиля.
Step 1 - Сформулируйте Truth table для данной логической функции.
Step 2 - В приведенной выше таблице истинности добавьте (включите) еще один столбец, который показывает связь между weighted sums и Threshold value.
Step 3 - Запишите соотношение между взвешенными суммами и порогом для каждой комбинации входных данных, как указано ниже.
Если выход логической функции равен 1, то взвешенная сумма будет больше или равна пороговому значению для этой комбинации входов.
Если выход логической функции равен 0, то взвешенная сумма будет меньше порогового значения для этой комбинации входов.
Step 4 - Выберите значения весов и порога таким образом, чтобы они удовлетворяли всем отношениям, представленным в последнем столбце приведенной выше таблицы.
step 5 - Нарисуйте symbol порогового строба с этими весами и пороговым значением.
пример
Реализуем следующие Boolean function с использованием одиночного порогового гейта.
$$Y\left ( X_{1},X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$$
Данная логическая функция является функцией трех переменных, которая представлена в виде суммы минимальных членов. ВTruth table этой функции показано ниже.
| Входы | Вывод | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Теперь давайте добавим (включим) еще один столбец в приведенную выше таблицу истинности. Этот последний столбец содержит отношения междуweighted sums (W) and Threshold значение (T) для каждой комбинации входов.
| Входы | Вывод | Отношения между W&T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <Т |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <Т |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ Т |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ Т |
Ниже приведены выводы из приведенной выше таблицы.
Значение порога должно быть либо нулевым, либо отрицательным в зависимости от первого отношения.
Значение W 3 должно быть отрицательным на основании первого и второго соотношений.
Значения W 1 и W 2 должны быть больше или равны пороговому значению на основе пятого и третьего соотношений.
W 2 должен быть больше W 3 на основании четвертого соотношения.
Мы можем выбрать следующие значения для весов и пороговых значений, основываясь на сделанных выше выводах.
W 1 = 2, W 2 = 1, W 3 = -4 и T = -1
В symbol Порогового строба с указанными выше значениями показано ниже.

Следовательно, этот пороговый вентиль реализует данный Boolean function, $Y\left ( X_{1}, X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$.
В предыдущих главах мы обсуждали различные комбинационные схемы. Все эти схемы имеют набор выходов, который зависит только от комбинации имеющихся входов. На следующем рисунке показанblock diagram последовательного контура.
Эта последовательная схема содержит набор входов и выходов. Выход (ы) последовательной схемы зависит не только от комбинации имеющихся входов, но также и от предыдущего выхода (ов). Предыдущий вывод - это не что иное, какpresent state. Следовательно, последовательные схемы содержат комбинационные схемы вместе с элементами памяти (хранилища). Некоторые последовательные схемы могут не содержать комбинационных схем, а только элементы памяти.
В следующей таблице показаны differences между комбинационными схемами и последовательными схемами.
| Комбинационные схемы | Последовательные схемы |
|---|---|
| Выходы зависят только от текущих входов. | Выходы зависят как от текущих входов, так и от текущего состояния. |
| Обратной связи нет. | Обратная связь присутствует. |
| Элементы памяти не требуются. | Требуются элементы памяти. |
| Тактовый сигнал не требуется. | Требуется тактовый сигнал. |
| Легко проектировать. | Сложно проектировать. |
Типы последовательных цепей
Ниже приведены два типа последовательных цепей -
- Асинхронные последовательные схемы
- Синхронные последовательные схемы
Асинхронные последовательные схемы
Если некоторые или все выходы последовательной схемы не изменяются (не влияют) относительно активного перехода синхросигнала, то эта последовательная схема называется Asynchronous sequential circuit. Это означает, что все выходы асинхронных последовательных схем не изменяются (не влияют) одновременно. Следовательно, большинство выходов асинхронных последовательных схем являютсяnot in synchronous либо только с положительными фронтами, либо только с отрицательными фронтами тактового сигнала.
Синхронные последовательные схемы
Если все выходы последовательной схемы изменяются (влияют) относительно активного перехода тактового сигнала, то эта последовательная схема называется Synchronous sequential circuit. Это означает, что все выходы синхронных последовательных схем изменяются (влияют) одновременно. Следовательно, выходы синхронных последовательных схем синхронизированы либо только с положительными фронтами, либо только с отрицательными фронтами тактового сигнала.
Тактовый сигнал и запуск
В этом разделе давайте по очереди обсудим тактовый сигнал и типы запуска.
Тактовый сигнал
Тактовый сигнал является периодическим, и его время включения и время выключения не обязательно должны совпадать. Мы можем представить тактовый сигнал какsquare wave, когда его время включения и время выключения одинаковы. Этот тактовый сигнал показан на следующем рисунке.

На рисунке выше прямоугольная волна рассматривается как тактовый сигнал. Этот сигнал остается на высоком логическом уровне (5 В) в течение некоторого времени и остается на низком логическом уровне (0 В) в течение того же времени. Этот образец повторяется с некоторым периодом времени. В этом случаеtime period будет равняться либо удвоенному времени включения, либо удвоенному времени выключения.
Мы можем представить тактовый сигнал как train of pulses, когда время включения и время выключения не совпадают. Этот тактовый сигнал показан на следующем рисунке.

На рисунке выше последовательность импульсов рассматривается как тактовый сигнал. Этот сигнал остается на высоком логическом уровне (5 В) в течение некоторого времени и остается на низком логическом уровне (0 В) в другое время. Этот образец повторяется с некоторым периодом времени. В этом случаеtime period будет равняться сумме времени включения и времени выключения.
Обратный период времени тактового сигнала известен как frequencyтактового сигнала. Все последовательные схемы работают с тактовым сигналом. Таким образом, частота, на которой могут работать последовательные схемы, должна быть выбрана соответственно частоте тактового сигнала.
Типы срабатывания
Ниже приведены два возможных типа запуска, которые используются в последовательных схемах.
- Срабатывание по уровню
- Запуск по фронту
Срабатывание по уровню
Существует два уровня тактового сигнала, а именно высокий логический уровень и низкий логический уровень. Ниже приведены дваtypes of level triggering.
- Запуск по положительному уровню
- Запуск по отрицательному уровню
Если последовательная цепь работает с тактовым сигналом, когда она находится в Logic High, то этот тип запуска известен как Positive level triggering. Это выделено на рисунке ниже.
Если последовательная цепь работает с тактовым сигналом, когда она находится в Logic Low, то этот тип запуска известен как Negative level triggering. Он выделен на следующем рисунке.

Запуск по фронту
Есть два типа переходов, которые происходят в тактовом сигнале. Это означает, что синхронизирующий сигнал переходит либо с низкого логического уровня на высокий логический, либо с высокого логического уровня на низкий.
Ниже приведены два types of edge triggering на основе переходов тактового сигнала.
- Запуск по положительному фронту
- Запуск по отрицательному фронту
Если последовательная схема работает с тактовым сигналом, который переходит от низкого логического уровня к высокому логическому уровню, то такой тип запуска известен как Positive edge triggering. Это также называется запуском по нарастающему фронту. Это показано на следующем рисунке.

Если последовательная схема работает с тактовым сигналом, который переходит с высокого логического уровня на низкий логический, то такой тип запуска известен как Negative edge triggering. Это также называется запуском по заднему фронту. Это показано на следующем рисунке.

В следующих главах мы обсудим различные последовательные схемы в зависимости от типа запуска, который может в них использоваться.
Есть два типа элементов памяти в зависимости от типа запуска, который подходит для их работы.
- Latches
- Flip-flops
Защелки работают с разрешающим сигналом, который level sensitive. В то время как шлепанцы чувствительны к краям. О шлепанцах мы поговорим в следующей главе. Теперь давайте поговорим о SR Latch и D Latch один за другим.
Защелка SR
Защелка SR также называется Set Reset Latch. Эта защелка влияет на выходы до тех пор, пока разрешение E поддерживается на «1». Вcircuit diagram Защелки SR показан на следующем рисунке.
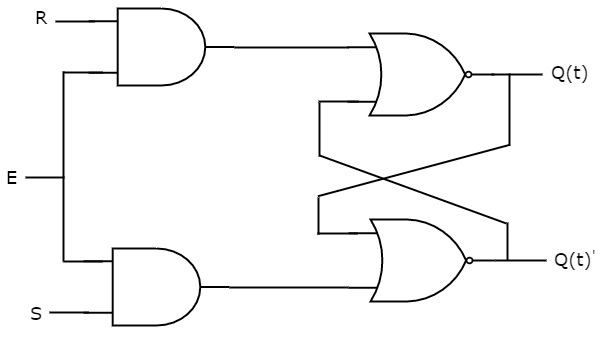
Эта схема имеет два входа S и R и два выхода Q (t) и Q (t) '. Вupper NOR gate имеет два входа R и дополнение текущего состояния, Q (t) ', и выдает следующее состояние, Q (t + 1), когда включено, E равно «1».
Точно так же lower NOR gate имеет два входа S и текущее состояние Q (t) и производит дополнение к следующему состоянию, Q (t + 1) 'при включении E равно' 1 '.
Мы знаем, что 2-input NOR gateпроизводит вывод, который является дополнением другого ввода, когда один из вводов равен «0». Точно так же он выдает «0» на выходе, когда один из входов равен «1».
Если S = 1, то следующее состояние Q (t + 1) будет равно «1» независимо от текущего состояния, значений Q (t).
Если R = 1, то следующее состояние Q (t + 1) будет равно «0» независимо от текущего состояния, значений Q (t).
В любой момент только из этих двух входов должен быть «1». Если оба входа равны «1», то значение следующего состояния Q (t + 1) не определено.
В следующей таблице показаны state table защелки SR.
| S | р | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (т) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Следовательно, SR Latch выполняет три типа функций, такие как удержание, установка и сброс, в зависимости от условий входа.
D Защелка
У SR Latch есть один недостаток. То есть следующее значение состояния не может быть предсказано, когда оба входа S и R являются одним. Таким образом, мы можем преодолеть эту трудность с помощью D Latch. Это также называется защелкой данных. Вcircuit diagram D-защелки показано на следующем рисунке.

Эта схема имеет один вход D и два выхода Q (t) и Q (t) '. D-защелка получается из SR-защелки, помещая инвертор между входами S amp; & R и подключая вход D к S. Это означает, что мы исключили комбинации S и R с одинаковым значением.
Если D = 0 → S = 0 & R = 1, то следующее состояние Q (t + 1) будет равно «0» независимо от текущего состояния, значений Q (t). Это соответствует второй строке таблицы состояний SR Latch.
Если D = 1 → S = 1 & R = 0, то следующее состояние Q (t + 1) будет равно «1» независимо от текущего состояния, значений Q (t). Это соответствует третьей строке таблицы состояний SR Latch.
В следующей таблице показаны state table защелки D.
| D | Q (t + 1) |
|---|---|
| 0 | 0 |
| 1 | 1 |
Следовательно, D Latch Удерживает информацию, которая доступна на входе данных, D. Это означает, что выход D Latch чувствителен к изменениям на входе, D, пока разрешение равно High.
В этой главе мы реализовали различные защелки, обеспечивая перекрестную связь между вентилями ИЛИ-НЕ. Точно так же вы можете реализовать эти защелки с помощью логических элементов NAND.
В предыдущей главе мы обсуждали защелки. Это основные строительные блоки шлепанцев. Мы можем реализовать триггеры двумя способами.
В первом методе cascade two latchesтаким образом, что первая защелка активируется для каждого положительного тактового импульса, а вторая защелка активируется для каждого отрицательного тактового импульса. Так что комбинация этих двух защелок превратилась в триггер.
Во втором методе мы можем напрямую реализовать триггер, чувствительный к краям. В этой главе давайте обсудим следующиеflip-flops используя второй метод.
- SR Flip-Flop
- D Вьетнамки
- JK Вьетнамки
- T Вьетнамки
SR Flip-Flop
SR-триггер работает только с положительными или отрицательными тактовыми переходами. При этом защелка SR работает с разрешающим сигналом. Вcircuit diagram триггера SR показан на следующем рисунке.

Эта схема имеет два входа S и R и два выхода Q (t) и Q (t) '. Триггер SR работает аналогично SR Latch. Но этот триггер влияет на выходы только тогда, когда применяется положительный переход синхросигнала вместо активного разрешения.
В следующей таблице показаны state table триггера SR.
| S | р | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (т) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Здесь Q (t) и Q (t + 1) представляют собой текущее состояние и следующее состояние соответственно. Таким образом, триггер SR может использоваться для одной из этих трех функций, таких как удержание, сброс и установка, в зависимости от условий входа, когда применяется положительный переход тактового сигнала. В следующей таблице показаныcharacteristic table триггера SR.
| Настоящие входы | Настоящее состояние | Следующее состояние | |
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | Икс |
| 1 | 1 | 1 | Икс |
Используя три переменных K-Map, мы можем получить упрощенное выражение для следующего состояния Q (t + 1). Вthree variable K-Map для следующего состояния Q (t + 1) показано на следующем рисунке.

Максимально возможные группировки соседних уже показаны на рисунке. Следовательноsimplified expression для следующего состояния Q (t + 1) равно
$Q\left ( t+1 \right )=S+{R}'Q\left ( t \right )$
D Вьетнамки
D-триггер работает только с положительными или отрицательными тактовыми переходами. При этом D-защелка работает с разрешающим сигналом. Это означает, что выход D-триггера нечувствителен к изменениям на входе D, за исключением активного перехода тактового сигнала. Вcircuit diagram D-триггера показан на следующем рисунке.

Эта схема имеет один вход D и два выхода Q (t) и Q (t) '. Работа D-триггера аналогична D-защелке. Но этот триггер влияет на выходы только тогда, когда применяется положительный переход синхросигнала вместо активного разрешения.
В следующей таблице показаны state table D триггер.
| D | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Следовательно, D-триггер всегда удерживает информацию, которая доступна на входе данных, D о более раннем положительном переходе тактового сигнала. Из приведенной выше таблицы состояний мы можем напрямую записать следующее уравнение состояния как
Q (t + 1) = D
Следующее состояние D-триггера всегда равно вводу данных, D для каждого положительного перехода тактового сигнала. Следовательно, D-триггеры могут использоваться в регистрах,shift registers и некоторые счетчики.
JK Вьетнамки
JK flip-flop - это модифицированная версия триггера SR. Он работает только с положительными или отрицательными тактовыми переходами. Вcircuit diagram триггера JK показан на следующем рисунке.
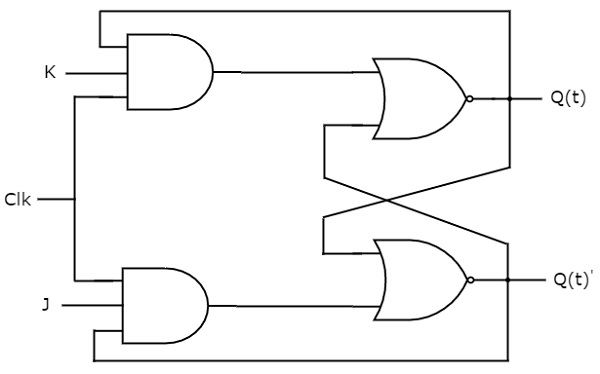
Эта схема имеет два входа J и K и два выхода Q (t) и Q (t) '. Триггер JK работает аналогично триггеру SR. Здесь мы рассмотрели входы SR-триггера какS = J Q(t)’ и R = KQ(t) чтобы использовать модифицированный триггер SR для 4 комбинаций входов.
В следующей таблице показаны state table JK вьетнамки.
| J | K | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (т) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q (t) ' |
Здесь Q (t) и Q (t + 1) представляют собой текущее состояние и следующее состояние соответственно. Итак, триггер JK может использоваться для одной из этих четырех функций, таких как удержание, сброс, установка и дополнение текущего состояния на основе входных условий, когда применяется положительный переход тактового сигнала. В следующей таблице показаныcharacteristic table JK вьетнамки.
| Настоящие входы | Настоящее состояние | Следующее состояние | |
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Используя три переменных K-Map, мы можем получить упрощенное выражение для следующего состояния Q (t + 1). Three variable K-Map для следующего состояния Q (t + 1) показано на следующем рисунке.

Максимально возможные группировки соседних уже показаны на рисунке. Следовательноsimplified expression для следующего состояния Q (t + 1) равно
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}'+{K}'Q\left ( t \right )$$
T Вьетнамки
T-триггер - это упрощенная версия JK-триггера. Это достигается подключением одного и того же входа «T» к обоим входам триггера JK. Он работает только с положительными или отрицательными тактовыми переходами. Вcircuit diagram T триггера показан на следующем рисунке.

Эта схема имеет один вход T и два выхода Q (t) и Q (t) '. Работа T-триггера такая же, как и у JK-триггера. Здесь мы рассмотрели входы триггера JK какJ = T и K = Tчтобы использовать модифицированный триггер JK для 2 комбинаций входов. Итак, мы исключили две другие комбинации J & K, для которых эти два значения дополняют друг друга в T-триггере.
В следующей таблице показаны state table T триггера.
| D | Q (t + 1) |
|---|---|
| 0 | Q (т) |
| 1 | Q (t) ' |
Здесь Q (t) и Q (t + 1) представляют собой текущее состояние и следующее состояние соответственно. Таким образом, T-триггер может использоваться для одной из этих двух функций, таких как удержание и дополнение текущего состояния на основе входных условий, когда применяется положительный переход тактового сигнала. В следующей таблице показаныcharacteristic table T триггера.
| Входы | Настоящее состояние | Следующее состояние |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Из приведенной выше таблицы характеристик мы можем напрямую записать next state equation в виде
$$Q\left ( t+1 \right )={T}'Q\left ( t \right )+TQ{\left ( t \right )}'$$
$$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
Выход T-триггера всегда переключается при каждом положительном переходе тактового сигнала, когда на входе T остается высокий логический уровень (1). Следовательно, T-триггер можно использовать вcounters.
В этой главе мы реализовали различные триггеры, обеспечив перекрестную связь между вентилями ИЛИ-НЕ. Точно так же вы можете реализовать эти триггеры, используя вентили NAND.
В предыдущей главе мы обсудили четыре триггера, а именно SR-триггер, D-триггер, JK-триггер и T-триггер. Мы можем преобразовать один триггер в оставшиеся три триггера, включив некоторую дополнительную логику. Итак, всего будет двенадцатьflip-flop conversions.
Следуйте этим steps для преобразования одного триггера в другой.
Рассмотрим characteristic table желаемого шлепанца.
Заполните значения возбуждения (входы) данного триггера для каждой комбинации текущего состояния и следующего состояния. Вexcitation table для всех шлепанцев показано ниже.
| Настоящее состояние | Следующее состояние | Входы для триггеров SR | Вход D-триггера | Входы для триггеров JK | T триггерный вход | ||
|---|---|---|---|---|---|---|---|
| Q(t) | Q(t+1) | S | R | D | J | K | T |
| 0 | 0 | 0 | Икс | 0 | 0 | Икс | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | Икс | 1 |
| 1 | 0 | 0 | 1 | 0 | Икс | 1 | 1 |
| 1 | 1 | Икс | 0 | 1 | Икс | 0 | 0 |
Получить simplified expressionsдля каждого входа возбуждения. При необходимости используйте Kmaps для упрощения.
Нарисуйте circuit diagram желаемого триггера в соответствии с упрощенными выражениями с использованием заданного триггера и необходимых логических вентилей.
А теперь давайте превратим несколько шлепанцев в другие. Выполните тот же процесс для оставшихся преобразований триггера.
SR Flip-Flop в другие преобразования Flip-Flop
Ниже приведены три возможных варианта преобразования триггера SR в другие триггеры.
- Триггер SR в триггер D
- Шлепанцы SR в шлепанцы JK
- Шлепанцы SR в триггеры T
Преобразование SR-триггера в D-триггер
Здесь данный триггер - это SR-триггер, а желаемый триггер - это D-триггер. Поэтому рассмотрим следующиеcharacteristic table D триггер.
| Вход D-триггера | Настоящее состояние | Следующее состояние |
|---|---|---|
| D | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мы знаем, что триггер SR имеет два входа S и R. Итак, запишите значения возбуждения триггера SR для каждой комбинации значений текущего состояния и следующего состояния. В следующей таблице показана таблица характеристик D-триггера вместе сexcitation inputs триггера SR.
| Вход D-триггера | Настоящее состояние | Следующее состояние | Входы для триггеров SR | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | S | R |
| 0 | 0 | 0 | 0 | Икс |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | Икс | 0 |
Из приведенной выше таблицы мы можем написать Boolean functions для каждого входа, как показано ниже.
$$S=m_{2}+d_{3}$$
$$R=m_{1}+d_{0}$$
Мы можем использовать 2 переменных K-Maps для получения упрощенных выражений для этих входных данных. Вk-Maps для S&R показаны ниже.

Итак, после упрощения мы получили S = D & R = D '. Вcircuit diagram D-триггера показан на следующем рисунке.

Эта схема состоит из триггера SR и инвертора. Этот инвертор выдает выходной сигнал, который является дополнением к входу D. Итак, вся схема имеет один вход D и два выхода Q (t) и Q (t) '. Следовательно, этоD flip-flop. Аналогичным образом вы можете выполнить два других преобразования.
D Преобразование триггеров в другие триггеры
Ниже приведены три возможных преобразования D-триггера в другие триггеры.
- D-триггер в T-триггер
- От D-триггера до SR-триггера
- D-триггер в JK-триггер
Преобразование D-триггера в T-триггер
Здесь данный триггер - это D триггер, а желаемый триггер - это T триггер. Поэтому рассмотрим следующиеcharacteristic table T триггера.
| T триггерный вход | Настоящее состояние | Следующее состояние |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мы знаем, что D-триггер имеет единственный вход D. Итак, запишите значения возбуждения D-триггера для каждой комбинации текущего состояния и значений следующего состояния. В следующей таблице показана таблица характеристик T-триггера вместе сexcitation input D триггер.
| T триггерный вход | Настоящее состояние | Следующее состояние | Вход D-триггера |
|---|---|---|---|
| T | Q(t) | Q(t + 1) | D |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
Из приведенной выше таблицы мы можем напрямую написать Boolean function из D, как показано ниже.
$$D=T\oplus Q\left ( t \right )$$
Итак, нам требуется вентиль с двумя входами «Исключающее ИЛИ» и D-триггер. Вcircuit diagram T триггера показан на следующем рисунке.

Эта схема состоит из D-триггера и логического элемента "исключающее ИЛИ". Этот вентиль «исключающее ИЛИ» производит вывод, который является исключающим ИЛИ для T и Q (t). Итак, вся схема имеет один вход T и два выхода Q (t) и Q (t) '. Следовательно, этоT flip-flop. Аналогичным образом вы можете выполнить два других преобразования.
JK Flip-Flop для других преобразований Flip-Flop
Ниже приведены три возможных варианта преобразования триггеров JK в другие триггеры.
- Вьетнамки JK в триггеры T
- Шлепанцы JK в шлепанцы D
- Вьетнамки JK к триггерам SR
JK flip-flop to T-flip-flop преобразование
Здесь данный триггер - это JK-триггер, а желаемый триггер - T-триггер. Поэтому рассмотрим следующиеcharacteristic table T триггера.
| T триггерный вход | Настоящее состояние | Следующее состояние |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мы знаем, что триггер JK имеет два входа J и K. Итак, запишите значения возбуждения триггера JK для каждой комбинации значений текущего и следующего состояния. В следующей таблице показана таблица характеристик T-триггера вместе сexcitation inputs JK триггер.
| T триггерный вход | Настоящее состояние | Следующее состояние | Входы для триггеров JK | |
|---|---|---|---|---|
| T | Q(t) | Q(t + 1) | J | K |
| 0 | 0 | 0 | 0 | Икс |
| 0 | 1 | 1 | Икс | 0 |
| 1 | 0 | 1 | 1 | Икс |
| 1 | 1 | 0 | Икс | 1 |
Из приведенной выше таблицы мы можем написать Boolean functions для каждого входа, как показано ниже.
$$J=m_{2}+d_{1}+d_{3}$$
$$K=m_{3}+d_{0}+d_{2}$$
Мы можем использовать 2 переменных K-Maps для получения упрощенных выражений для этих двух входов. Вk-Maps для J&K показаны ниже.

Итак, мы получили J = T & K = T после упрощения. Вcircuit diagram T триггера показан на следующем рисунке.

Эта схема состоит только из триггеров JK. Никаких других ворот не требует. Просто подключите один и тот же вход T к обоим J и K. Итак, вся схема имеет один вход T и два выхода Q (t) и Q (t) '. Следовательно, этоT flip-flop. Аналогичным образом вы можете выполнить два других преобразования.
T Flip-Flop в другие преобразования Flip-Flop
Ниже приведены три возможных преобразования Т-триггера в другие триггеры.
- T-триггер в D-триггер
- От T-триггера до SR-триггера
- От T-шлепанца до JK-шлепанца
Преобразование T-триггера в D-триггер
Здесь данный триггер - это T триггер, а желаемый триггер - это D триггер. Следовательно, рассмотрите характеристическую таблицу D-триггера и запишите значения возбуждения T-триггера для каждой комбинации текущего состояния и значений следующего состояния. В следующей таблице показаныcharacteristic table D-триггера вместе с excitation input T триггера.
| Вход D-триггера | Настоящее состояние | Следующее состояние | T триггерный вход | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | T | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | |
Из приведенной выше таблицы мы можем напрямую написать логическую функцию T, как показано ниже.
$$T=D\oplus Q\left ( t \right )$$
Итак, нам требуется вентиль с двумя входами «Исключающее ИЛИ» и T-триггер. Вcircuit diagram D-триггера показан на следующем рисунке.

Эта схема состоит из T-триггера и логического элемента "исключающее ИЛИ". Этот вентиль исключающего ИЛИ производит выходной сигнал, который является исключающим ИЛИ для D и Q (t). Итак, вся схема имеет один вход D и два выхода Q (t) и Q (t) '. Следовательно, этоD flip-flop. Аналогичным образом вы можете выполнить два других преобразования.
Мы знаем, что один триггер может хранить один бит информации. Чтобы хранить несколько битов информации, нам требуется несколько триггеров. Группа триггеров, которые используются для хранения (хранения) двоичных данных, известна какregister.
Если регистр может сдвигать биты в правую или левую сторону, это называется shift register. Регистр сдвига "N" битов содержит "N" триггеров. Ниже приведены четыре типа регистров сдвига, основанные на применении входов и доступе к выходам.
- Сдвиговый регистр Serial In - Serial Out
- Сдвиговый регистр Serial In - Parallel Out
- Регистр сдвига Parallel In - Serial Out
- Регистр сдвига Parallel In - Parallel Out
Регистр сдвига последовательного входа - выхода (SISO)
Регистр сдвига, который обеспечивает последовательный ввод и производит последовательный вывод, известен как Serial In - Serial Out. (SISO)регистр сдвига. Вblock diagram 3-битного регистра сдвига SISO показано на следующем рисунке.

Эта блок-схема состоит из трех D-триггеров, которые cascaded. Это означает, что выход одного D-триггера подключен как вход следующего D-триггера. Все эти триггеры синхронны друг с другом, поскольку к каждому из них применяется один и тот же тактовый сигнал.
В этом регистре сдвига мы можем посылать биты последовательно с входа самого левого D-триггера. Следовательно, этот вход также называетсяserial input. При каждом срабатывании тактового сигнала по положительному фронту данные переходят от одной ступени к другой. Итак, мы можем получать биты последовательно с выхода самого правого D-триггера. Следовательно, этот вывод также называетсяserial output.
пример
Давайте посмотрим, как работает 3-битный регистр сдвига SISO, отправив двоичную информацию “011” последовательно от LSB к MSB на входе.
Предположим, начальное состояние D-триггеров от крайнего левого до крайнего правого $Q_{2}Q_{1}Q_{0}=000$. Мы можем понятьworking of 3-bit SISO shift register from the following table.
| No of positive edge of Clock | Serial Input | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1(LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0(MSB) | 0 | 1 | 1(LSB) |
| 4 | - | - | 0 | 1 |
| 5 | - | - | - | 0(MSB) |
The initial status of the D flip-flops in the absence of clock signal is $Q_{2}Q_{1}Q_{0}=000$. Here, the serial output is coming from $Q_{0}$. So, the LSB (1) is received at 3rd positive edge of clock and the MSB (0) is received at 5th positive edge of clock.
Therefore, the 3-bit SISO shift register requires five clock pulses in order to produce the valid output. Similarly, the N-bit SISO shift register requires 2N-1 clock pulses in order to shift ‘N’ bit information.
Serial In - Parallel Out (SIPO) Shift Register
The shift register, which allows serial input and produces parallel output is known as Serial In – Parallel Out (SIPO) shift register. The block diagram of 3-bit SIPO shift register is shown in the following figure.
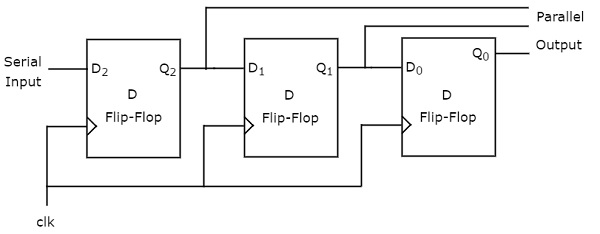
This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can send the bits serially from the input of left most D flip-flop. Hence, this input is also called as serial input. For every positive edge triggering of clock signal, the data shifts from one stage to the next. In this case, we can access the outputs of each D flip-flop in parallel. So, we will get parallel outputs from this shift register.
Example
Let us see the working of 3-bit SIPO shift register by sending the binary information “011” from LSB to MSB serially at the input.
Assume, initial status of the D flip-flops from leftmost to rightmost is $Q_{2}Q_{1}Q_{0}=000$. Here, $Q_{2}$ & $Q_{0}$ are MSB & LSB respectively. We can understand the working of 3-bit SIPO shift register from the following table.
| No of positive edge of Clock | Serial Input | Q2(MSB) | Q1 | Q0(LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1(LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0(MSB) | 0 | 1 | 1 |
The initial status of the D flip-flops in the absence of clock signal is $Q_{2}Q_{1}Q_{0}=000$. The binary information “011” is obtained in parallel at the outputs of D flip-flops for third positive edge of clock.
So, the 3-bit SIPO shift register requires three clock pulses in order to produce the valid output. Similarly, the N-bit SIPO shift register requires N clock pulses in order to shift ‘N’ bit information.
Parallel In − Serial Out (PISO) Shift Register
The shift register, which allows parallel input and produces serial output is known as Parallel In − Serial Out (PISO) shift register. The block diagram of 3-bit PISO shift register is shown in the following figure.

This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can apply the parallel inputs to each D flip-flop by making Preset Enable to 1. For every positive edge triggering of clock signal, the data shifts from one stage to the next. So, we will get the serial output from the right most D flip-flop.
Example
Let us see the working of 3-bit PISO shift register by applying the binary information “011” in parallel through preset inputs.
Since the preset inputs are applied before positive edge of Clock, the initial status of the D flip-flops from leftmost to rightmost will be $Q_{2}Q_{1}Q_{0}=011$. We can understand the working of 3-bit PISO shift register from the following table.
| No of positive edge of Clock | Q2 | Q1 | Q0 |
|---|---|---|---|
| 0 | 0 | 1 | 1(LSB) |
| 1 | - | 0 | 1 |
| 2 | - | - | 0(LSB) |
Here, the serial output is coming from $Q_{0}$. So, the LSB (1) is received before applying positive edge of clock and the MSB (0) is received at 2nd positive edge of clock.
Therefore, the 3-bit PISO shift register requires two clock pulses in order to produce the valid output. Similarly, the N-bit PISO shift register requires N-1 clock pulses in order to shift ‘N’ bit information.
Parallel In - Parallel Out (PIPO) Shift Register
The shift register, which allows parallel input and produces parallel output is known as Parallel In − Parallel Out (PIPO) shift register. The block diagram of 3-bit PIPO shift register is shown in the following figure.

This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can apply the parallel inputs to each D flip-flop by making Preset Enable to 1. We can apply the parallel inputs through preset or clear. These two are asynchronous inputs. That means, the flip-flops produce the corresponding outputs, based on the values of asynchronous inputs. In this case, the effect of outputs is independent of clock transition. So, we will get the parallel outputs from each D flip-flop.
пример
Давайте посмотрим, как работает 3-битный регистр сдвига PIPO, применяя двоичную информацию “011” параллельно через предустановленные входы.
Поскольку предустановленные входы применяются до положительного фронта тактового сигнала, начальное состояние D-триггеров от крайнего левого до крайнего правого будет $Q_{2}Q_{1}Q_{0}=011$. Итак, двоичная информация“011” получается параллельно на выходах D-триггеров до подачи положительного фронта тактового сигнала.
Следовательно, 3-битный регистр сдвига PIPO требует нулевых тактовых импульсов для получения действительного выхода. Точно так жеN-bit PIPO shift register не требует никаких тактовых импульсов для сдвига информации «N» битов.
В предыдущей главе мы обсудили четыре типа регистров сдвига. В зависимости от требований мы можем использовать один из этих регистров сдвига. Ниже приведены применения регистров сдвига.
Регистр сдвига используется как Parallel to serial converter, который преобразует параллельные данные в последовательные. Он используется в секции передатчика после блока аналого-цифрового преобразователя (АЦП).
Регистр сдвига используется как Serial to parallel converter, который преобразует последовательные данные в параллельные. Он используется в секции приемника перед блоком цифро-аналогового преобразователя (ЦАП).
Регистр сдвига вместе с некоторыми дополнительными вентилями генерирует последовательность нулей и единиц. Следовательно, он используется какsequence generator.
Регистры сдвига также используются как counters. Есть два типа счетчиков в зависимости от типа выхода из крайнего правого D-триггера, подключенного к последовательному входу. Это счетчик Ring и счетчик Johnson Ring.
В этой главе давайте обсудим эти два счетчика один за другим.
Счетчик звонков
В предыдущей главе мы обсуждали работу последовательного входа - параллельного выхода. (SIPO)регистр сдвига. Он принимает данные извне в последовательной форме и требует «N» тактовых импульсов для сдвига данных «N» битов.
Так же, ‘N’ bit Ring counterвыполняет аналогичную операцию. Но единственное отличие состоит в том, что выход крайнего правого D-триггера задается как вход крайнего левого D-триггера, вместо того, чтобы применять данные извне. Таким образом, счетчик звонков выдает последовательность состояний (набор нулей и единиц), и он повторяется для каждого‘N’ clock cycles.
В block diagram 3-битного счетчика звонков показан на следующем рисунке.
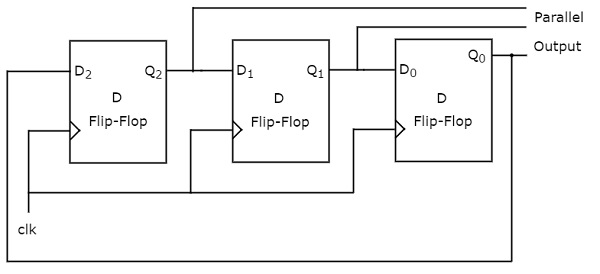
3-битный счетчик звонков содержит только 3-битный регистр сдвига SIPO. Выход крайнего правого D-триггера подключен к последовательному входу самого левого D-триггера.
Предположим, начальное состояние D-триггеров от крайнего левого до крайнего правого $Q_{2}Q_{1}Q_{0}=001$. Вот,$Q_{2}$ & $Q_{0}$равны MSB и LSB соответственно. Мы можем понятьworking of Ring counter из следующей таблицы.
| Нет положительного фронта часов | Последовательный ввод = Q 0 | Q 2 (MSB) | Q 1 | Q 0 (младший бит) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 |
Первоначальное состояние D-триггеров при отсутствии тактового сигнала: $Q_{2}Q_{1}Q_{0}=001$. Это состояние повторяется для каждых трех положительных переходов фронта тактового сигнала.
Следовательно, следующие operations имеют место для каждого положительного фронта тактового сигнала.
Последовательный ввод первого D-триггера получает предыдущий вывод третьего триггера. Таким образом, текущий выход первого D-триггера равен предыдущему выходному сигналу третьего триггера.
Предыдущие выходы первого и второго D-триггеров сдвинуты вправо на один бит. Это означает, что текущие выходы второго и третьего D-триггеров равны предыдущим выходам первого и второго D-триггеров.
Счетчик кольца Джонсона
Работа Johnson Ring counterаналогичен кольцевому счетчику. Но с той лишь разницей, что дополненный выход крайнего правого D-триггера задается как вход крайнего левого D-триггера вместо обычного выхода. Следовательно, N-битный счетчик Johnson Ring формирует последовательность состояний (набор нулей и единиц), и она повторяется для каждого‘2N’ clock cycles.
Счетчик Johnson Ring также называют Twisted Ring counterи переключить счетчик хвостового кольца. Вblock diagram 3-битного счетчика Johnson Ring показан на следующем рисунке.

3-битный счетчик Johnson Ring также содержит только 3-битный регистр сдвига SIPO. Дополненный выход крайнего правого D-триггера соединен с последовательным входом крайнего левого D-триггера.
Предположим, что изначально все D-триггеры сброшены. Так,$Q_{2}Q_{1}Q_{0}=000$. Вот,$Q_{2}$ & $Q_{0}$равны MSB и LSB соответственно. Мы можем понятьworking счетчика Johnson Ring из следующей таблицы.
| Нет положительного фронта часов | Последовательный ввод = Q 0 | Q 2 (MSB) | Q 1 | Q 0 (младший бит) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 |
Первоначальное состояние D-триггеров при отсутствии тактового сигнала: $Q_{2}Q_{1}Q_{0}=000$. Это состояние повторяется для каждых шести положительных переходов фронта тактового сигнала.
Следовательно, следующие operations имеют место для каждого положительного фронта тактового сигнала.
Последовательный ввод первого D-триггера получает предыдущий дополненный вывод третьего триггера. Таким образом, текущий выходной сигнал первого D-триггера равен предыдущему дополненному выходному сигналу третьего триггера.
Предыдущие выходы первого и второго D-триггеров сдвинуты вправо на один бит. Это означает, что текущие выходы второго и третьего D-триггеров равны предыдущим выходам первого и второго D-триггеров.
В предыдущих двух главах мы обсуждали различные регистры сдвига и counters using D flipflops. Теперь давайте обсудим различные счетчики, использующие T-триггеры. Мы знаем, что T-триггер переключает выход либо для каждого положительного фронта тактового сигнала, либо для отрицательного фронта тактового сигнала.
Двоичный счетчик N битов состоит из N T триггеров. Если счетчик считает от 0 до 2 - 1, тогда он называется двоичным up counter. Аналогично, если счетчик ведет обратный отсчет от 2 - от 1 до 0, тогда он называется двоичным down counter.
Есть два types of counters на основе триггеров, которые подключены синхронно или нет.
- Асинхронные счетчики
- Синхронные счетчики
Асинхронные счетчики
Если триггеры не получают одинаковый тактовый сигнал, то этот счетчик вызывается как Asynchronous counter. Выход системных часов используется как тактовый сигнал только для первого триггера. Остальные триггеры получают тактовый сигнал с выхода триггера предыдущего каскада. Следовательно, выходы всех триггеров не изменяются (не влияют) одновременно.
Теперь давайте обсудим следующие два счетчика один за другим.
- Асинхронный двоичный счетчик вверх
- Асинхронный двоичный обратный счетчик
Асинхронный двоичный счетчик увеличения
Асинхронный двоичный восходящий счетчик битов N состоит из N T триггеров. Считается от 0 до 2 - 1. block diagram 3-битного асинхронного двоичного восходящего счетчика показано на следующем рисунке.

3-битный асинхронный двоичный восходящий счетчик содержит три T-триггера, а вход T всех триггеров соединен с «1». Все эти триггеры срабатывают по отрицательному фронту, но выходы меняются асинхронно. Тактовый сигнал подается непосредственно на первый T-триггер. Итак, выход первого T триггераtoggles для каждого отрицательного фронта тактового сигнала.
Выход первого T-триггера используется как тактовый сигнал для второго T-триггера. Таким образом, выход второго T-триггера переключается для каждого отрицательного фронта выхода первого T-триггера. Точно так же выход третьего T-триггера переключается для каждого отрицательного фронта выхода второго T-триггера, поскольку выход второго T-триггера действует как тактовый сигнал для третьего T-триггера.
Предположим, что начальное состояние T триггеров от крайнего правого до крайнего левого равно $Q_{2}Q_{1}Q_{0}=000$. Вот,$Q_{2}$ & $Q_{0}$равны MSB и LSB соответственно. Мы можем понятьworking 3-битного асинхронного двоичного счетчика из следующей таблицы.
| Нет отрицательного фронта часов | Q 0 (младший бит) | Q 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 |
| 7 | 1 | 1 | 1 |
Вот $Q_{0}$ переключается для каждого отрицательного фронта тактового сигнала. $Q_{1}$ переключается для каждого $Q_{0}$который изменяется от 1 до 0, в противном случае остается в предыдущем состоянии. Так же,$Q_{2}$ переключается для каждого $Q_{1}$ который изменяется от 1 до 0, в противном случае остается в предыдущем состоянии.
Исходное состояние T-триггеров при отсутствии тактового сигнала: $Q_{2}Q_{1}Q_{0}=000$. Оно увеличивается на единицу для каждого отрицательного фронта тактового сигнала и достигает максимального значения на 7- м отрицательном фронте тактового сигнала. Этот шаблон повторяется, когда применяются дополнительные отрицательные фронты тактового сигнала.
Асинхронный двоичный счетчик вниз
Асинхронный двоичный обратный счетчик битов N состоит из N T триггеров. Считается от 2 - от 1 до 0. block diagram 3-битного асинхронного двоичного обратного счетчика показано на следующем рисунке.

Блок-схема 3-битного асинхронного двоичного обратного счетчика аналогична блок-схеме 3-битного асинхронного двоичного обратного счетчика. Но единственное отличие состоит в том, что вместо подключения обычных выходов одного каскадного триггера в качестве тактового сигнала для следующего каскадного триггера, подключитеcomplemented outputsодного каскадного триггера в качестве тактового сигнала для следующего каскадного триггера. Дополненный вывод изменяется от 1 до 0, так же как нормальный вывод изменяется от 0 до 1.
Предположим, что начальное состояние T триггеров от крайнего правого до крайнего левого равно $Q_{2}Q_{1}Q_{0}=000$. Вот,$Q_{2}$ & $Q_{0}$равны MSB и LSB соответственно. Мы можем понятьworking 3-битного асинхронного двоичного обратного счетчика из следующей таблицы.
| Нет отрицательного фронта часов | Q 0 (младший бит) | Q 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 1 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 |
Вот $Q_{0}$ переключается для каждого отрицательного фронта тактового сигнала. $Q_{1}$ переключается для каждого $Q_{0}$который изменяется от 0 до 1, в противном случае остается в предыдущем состоянии. Так же,$Q_{2}$ переключается для каждого $Q_{1}$ который изменяется от 0 до 1, в противном случае остается в предыдущем состоянии.
Исходное состояние T-триггеров при отсутствии тактового сигнала: $Q_{2}Q_{1}Q_{0}=000$. Оно уменьшается на единицу для каждого отрицательного фронта тактового сигнала и достигает того же значения на 8- м отрицательном фронте тактового сигнала. Этот шаблон повторяется, когда применяются дополнительные отрицательные фронты тактового сигнала.
Синхронные счетчики
Если все триггеры получают один и тот же тактовый сигнал, то этот счетчик вызывается как Synchronous counter. Следовательно, выходы всех триггеров изменяются (влияют) одновременно.
Теперь давайте обсудим следующие два счетчика один за другим.
- Синхронный двоичный счетчик вверх
- Синхронный двоичный обратный счетчик
Синхронный двоичный счетчик вверх
N-битный синхронный двоичный восходящий счетчик состоит из N T триггеров. Считается от 0 до 2 - 1. block diagram 3-битного синхронного двоичного восходящего счетчика показано на следующем рисунке.

3-битный синхронный двоичный повышающий счетчик содержит три T-триггера и один логический элемент И с 2 входами. Все эти триггеры запускаются по отрицательному фронту, и выходы триггеров изменяются (воздействуют) синхронно. Входы T первого, второго и третьего триггеров равны 1,$Q_{0}$ & $Q_{1}Q_{0}$ соответственно.
Выход первого T триггера togglesдля каждого отрицательного фронта тактового сигнала. Выход второго T-триггера переключается для каждого отрицательного фронта тактового сигнала, если$Q_{0}$ равно 1. Выход третьего T-триггера переключается для каждого отрицательного фронта тактового сигнала, если оба $Q_{0}$ & $Q_{1}$ 1.
Синхронный двоичный счетчик вниз
Синхронный двоичный обратный счетчик битов N состоит из N T триггеров. Считается от 2 - от 1 до 0. block diagram 3-битного синхронного двоичного обратного счетчика показано на следующем рисунке.

3-битный синхронный двоичный обратный счетчик содержит три T триггера и один логический элемент И с 2 входами. Все эти триггеры запускаются по отрицательному фронту, и выходы триггеров изменяются (воздействуют) синхронно. Входы T первого, второго и третьего триггеров равны 1,${Q_{0}}'$ & ' ${Q_{1}}'$${Q_ {0}} '$ соответственно.
Выход первого T триггера togglesдля каждого отрицательного фронта тактового сигнала. Выход второго T-триггера переключается для каждого отрицательного фронта тактового сигнала, если $ {Q_ {0}} '$ is 1. The output of third T flip-flop toggles for every negative edge of clock signal if both ${Q_ {1}} '$ & ${Q_ {0}} '$ равно 1.
Мы знаем, что синхронные последовательные схемы изменяют (влияют) на свои состояния при каждом положительном (или отрицательном) переходе тактового сигнала в зависимости от входа. Таким образом, это поведение синхронных последовательных схем может быть представлено в графической форме, и оно известно какstate diagram.
Синхронная последовательная схема также называется Finite State Machine(Автомат), если он имеет конечное число состояний. Есть два типа конечных автоматов.
- Конечный автомат Мили
- Конечный автомат Мура
Теперь давайте обсудим эти два конечных автомата один за другим.
Конечный автомат Мили
Конечный автомат называется конечным автоматом Мили, если выходы зависят как от текущих входов, так и от текущих состояний. Вblock diagram Конечный автомат Мили показан на следующем рисунке.
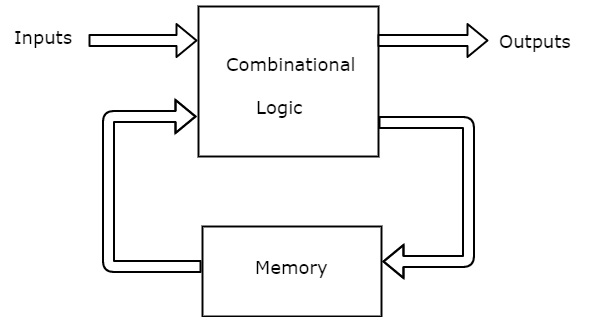
Как показано на рисунке, в конечном автомате Мили присутствуют две части. Это комбинационная логика и память. Память полезна для предоставления некоторых или части предыдущих результатов(present states) как входы комбинационной логики.
Итак, на основе текущих входных данных и текущих состояний конечный автомат Мили выдает выходные данные. Следовательно, выходы будут действительны только при положительном (или отрицательном) переходе тактового сигнала.
В state diagram Конечный автомат Мили показан на следующем рисунке.
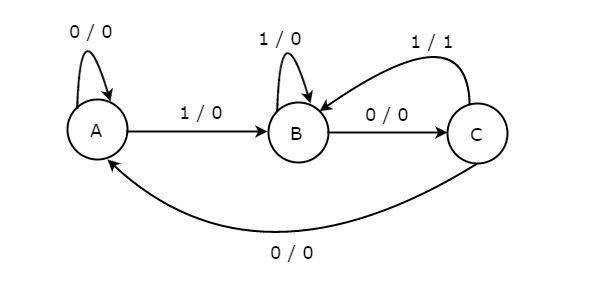
На приведенном выше рисунке есть три состояния, а именно A, B и C. Эти состояния помечены внутри кружков, и каждый кружок соответствует одному состоянию. Переходы между этими состояниями изображены направленными линиями. Здесь 0/0, 1/0 и 1/1 обозначаютinput / output. На приведенном выше рисунке есть два перехода из каждого состояния в зависимости от значения ввода x.
В общем, количество состояний, требуемых в конечном автомате Мили, меньше или равно количеству состояний, необходимых для конечного автомата Мура. Для каждого конечного автомата Мили существует эквивалентный конечный автомат Мура.
Конечный автомат Мура
Конечный автомат называется конечным автоматом Мура, если выходные данные зависят только от текущих состояний. Вblock diagram Конечный автомат Мура показан на следующем рисунке.

Как показано на рисунке, в конечном автомате Мура присутствуют две части. Это комбинационная логика и память. В этом случае текущие входы и текущие состояния определяют следующие состояния. Итак, на основе следующих состояний конечный автомат Мура производит выходные данные. Следовательно, выходы будут действительными только после перехода из состояния.
В state diagram Конечный автомат Мура показан на следующем рисунке.

На приведенном выше рисунке есть четыре состояния, а именно A, B, C и D. Эти состояния и соответствующие выходы помечены внутри кружков. Здесь на каждом переходе помечено только входное значение. На приведенном выше рисунке есть два перехода из каждого состояния в зависимости от значения ввода x.
В общем, количество состояний, требуемых в конечном автомате Мура, больше или равно количеству состояний, необходимых для конечного автомата Мили. Для каждого конечного автомата Мура существует эквивалентный конечный автомат Мили. Итак, исходя из требований, мы можем использовать один из них.
Каждые digital systemможно разделить на две части. Это цепи передачи данных (цифровые) и схемы управления. Цепи тракта данных выполняют такие функции, как хранение двоичной информации (данных) и передача данных из одной системы в другую. Тогда как схемы управления определяют поток операций цифровых схем.
С помощью диаграмм состояний сложно описать поведение больших конечных автоматов. Чтобы преодолеть эту трудность, можно использовать графики алгоритмического конечного автомата (ASM).ASM chartsпохожи на блок-схемы. Они используются для представления потока задач, которые должны выполняться цепями тракта данных и цепями управления.
Основные компоненты диаграмм ASM
Ниже приведены три основных компонента диаграмм ASM.
- Государственная коробка
- Коробка решения
- Поле условного вывода
Государственная коробка
Коробка состояний представлена в прямоугольной форме. Каждый блок состояний представляет одно состояние последовательной схемы. Вsymbol поля состояния показано на следующем рисунке.
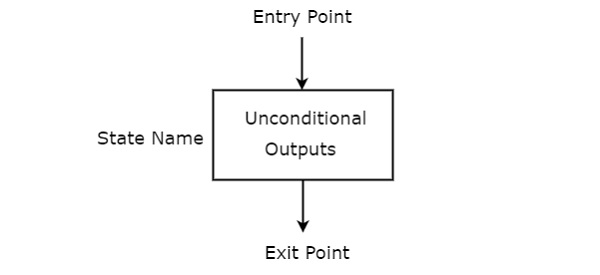
Он имеет одну точку входа и одну точку выхода. Название штата помещается слева от поля состояния. Безусловные выходы, соответствующие этому состоянию, могут быть помещены в поле состояния.Moore Выходы конечного автомата также могут быть помещены внутри блока состояний.
Коробка решения
Окно решения представлено ромбовидной формой. Вsymbol окна решения показано на следующем рисунке.

У него одна точка входа и два пути выхода. Входные данные или логические выражения могут быть помещены в поле принятия решения, где необходимо проверить, истинны они или ложны. Если условие истинно, то предпочтение будет отдано path1. В противном случае он предпочтет path2.
Поле условного вывода
Поле условного вывода имеет овальную форму. Вsymbol окна условного вывода показано на следующем рисунке.

Он также имеет одну точку входа и одну точку выхода, аналогичную блоку состояния. Условные выходы могут быть помещены в поле состояния. В общем,MealyВыходы конечного автомата представлены внутри окна условного вывода. Итак, исходя из требований, мы можем правильно использовать вышеуказанные компоненты для рисования диаграмм ASM.