Теория сети - Эквивалентные схемы
Если схема состоит из двух или более одинаковых пассивных элементов и соединены исключительно последовательно или параллельно, то мы можем заменить их одним эквивалентным пассивным элементом. Следовательно, эта схема называетсяequivalent circuit.
В этой главе давайте обсудим следующие две эквивалентные схемы.
- Последовательная эквивалентная схема
- Параллельная эквивалентная схема
Последовательная эквивалентная схема
Если аналогичные пассивные элементы подключены в series, то через все эти элементы будет течь одинаковый ток. Но напряжение делится на каждый элемент.
Рассмотрим следующее circuit diagram.
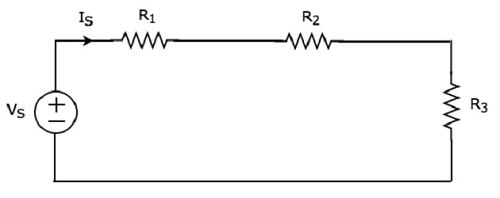
Он имеет один источник напряжения (V S ) и три резистора с сопротивлением R 1 , R 2 и R 3 . Все эти элементы соединены последовательно. Текущий IS протекает через все эти элементы.
В приведенной выше схеме есть только одна сетка. ВKVL equation вокруг этой сетки
$$ V_S = V_1 + V_2 + V_3 $$
Подставьте $ V_1 = I_S R_1, \: V_2 = I_S R_2 $ и $ V_3 = I_S R_3 $ в приведенное выше уравнение.
$$ V_S = I_S R_1 + I_S R_2 + I_S R_3 $$
$$ \ Rightarrow V_S = I_S (R_1 + R_2 + R_3) $$
Вышеприведенное уравнение имеет вид $ V_S = I_S R_ {Eq} $, где,
$$ R_ {Eq} = R_1 + R_2 + R_3 $$
В equivalent circuit diagram данной схемы показана на следующем рисунке.
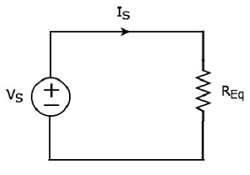
Это означает, что если несколько резисторов подключены последовательно, мы можем заменить их на equivalent resistor. Сопротивление этого эквивалентного резистора равно сумме сопротивлений всех этих нескольких резисторов.
Note 1- Если индуктивности N, имеющие индуктивности L 1 , L 2 , ..., L N , подключены последовательно, тоequivalent inductance будет
$$ L_ {Eq} = L_1 + L_2 + ... + L_N $$
Note 2- Если N конденсаторов емкостью C 1 , C 2 , ..., C N подключены последовательно, тоequivalent capacitance будет
$$ \ frac {1} {C_ {Eq}} = \ frac {1} {C_1} + \ frac {1} {C_2} + ... + \ frac {1} {C_N} $$
Параллельная эквивалентная схема
Если аналогичные пассивные элементы подключены в parallel, то на каждом элементе будет поддерживаться одинаковое напряжение. Но ток, протекающий через каждый элемент, разделяется.
Рассмотрим следующее circuit diagram.

Он имеет один источник тока (I S ) и три резистора с сопротивлением R 1 , R 2 и R 3 . Все эти элементы соединены параллельно. Напряжение (V S ) доступно на всех этих элементах.
Вышеупомянутая схема имеет только один главный узел (P), кроме наземного. ВKCL equation в этом главном узле (P)
$$ I_S = I_1 + I_2 + I_3 $$
Подставьте $ I_1 = \ frac {V_S} {R_1}, \: I_2 = \ frac {V_S} {R_2} $ и $ I_3 = \ frac {V_S} {R_3} $ в приведенное выше уравнение.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} + \ frac {V_S} {R_3} $$
$$ \ Rightarrow I_S = V_S \ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ left [\ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} \ right] $$
Вышеупомянутое уравнение имеет вид V S = I S R Eq, где,
$$ R_ {Eq} = \ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} $$
$$ \ frac {1} {R_ {Eq}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} $$
В equivalent circuit diagram данной схемы показана на следующем рисунке.
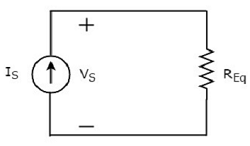
Это означает, что если несколько резисторов подключены параллельно, мы можем заменить их эквивалентным резистором. Сопротивление этогоequivalent resistor равно обратной величине суммы, обратной каждому сопротивлению всех этих нескольких резисторов.
Note 1- Если индуктивности N с индуктивностями L 1 , L 2 , ..., L N подключены параллельно, тоequivalent inductance будет
$$ \ frac {1} {L_ {Eq}} = \ frac {1} {L_1} + \ frac {1} {L_2} + ... + \ frac {1} {L_N} $$
Note 2- Если N конденсаторов емкостью C 1 , C 2 , ..., C N подключены параллельно, тоequivalent capacitance будет
$$ C_ {Eq} = C_1 + C_2 + ... + C_N $$