Теория сети - Анализ сетки
При анализе сетки мы будем рассматривать токи, протекающие через каждую сетку. Следовательно, анализ сетки также называютMesh-current method.
А branch- это путь, соединяющий два узла и содержащий элемент схемы. Если ветвь принадлежит только одной сетке, то ток ветки будет равен току сетки.
Если ветвь является общей для двух сеток, то ток ответвления будет равен сумме (или разности) двух токов сетки, когда они находятся в одном (или противоположном) направлении.
Процедура анализа сетки
Выполните эти шаги при решении любой электрической сети или цепи с помощью анализа сетки.
Step 1 - Определите meshes и обозначьте токи в сетке по часовой стрелке или против часовой стрелки.
Step 2 - Обратите внимание на величину тока, протекающего через каждый элемент, с точки зрения токов сетки.
Step 3 - написать mesh equationsко всем сеткам. Уравнение сетки получается применением сначала КВЛ, а затем закона Ома.
Step 4 - Решите сеточные уравнения, полученные на шаге 3, чтобы получить mesh currents.
Теперь мы можем найти ток, протекающий через любой элемент, и напряжение на любом элементе, который присутствует в данной сети, с помощью ячеистых токов.
пример
Найдите напряжение на резисторе 30 Ом, используя Mesh analysis.
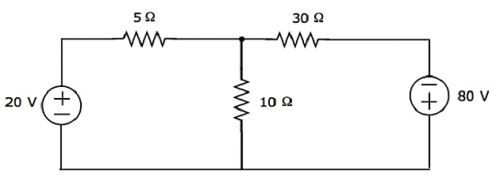
Step 1- В приведенной выше схеме есть две сетки. Вmesh currentsI 1 и I 2 считаются по часовой стрелке. Эти сеточные токи показаны на следующем рисунке.
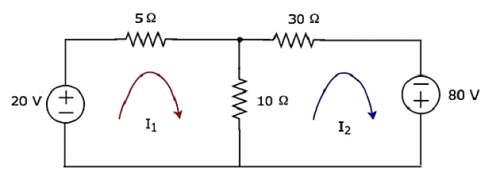
Step 2- Сеточный ток I 1 протекает через источник напряжения 20 В и резистор 5 Ом. Точно так же сеточный ток I 2 протекает через резистор 30 Ом и источник напряжения -80 В. Но разница двух токов сетки, I 1 и I 2 , протекает через резистор 10 Ом, поскольку это общая ветвь двух сеток.
Step 3 - В этом случае мы получим two mesh equationsпоскольку в данной схеме две сетки. Когда мы пишем уравнения сетки, предполагаем, что ток сетки этой конкретной сетки больше, чем токи всех других сеток схемы.
В mesh equation первой сетки
$$ 20 - 5I_1 -10 (I_1 - I_2) = 0 $$
$$ \ Rightarrow 20 - 15I_1 + 10I_2 = 0 $$
$$ \ Rightarrow 10I_2 = 15I_1 - 20 $$
Разделите приведенное выше уравнение на 5.
$$ 2I_2 = 3I_1 - 4 $$
Умножьте полученное выше уравнение на 2.
4I_2 = 6I_1 - 8 $ Equation 1
В mesh equation второй сетки
$$ - 10 (I_2 - I_1) - 30I_2 + 80 = 0 $$
Разделите полученное выше уравнение на 10.
$$ - (I_2 - I_1) - 3I_2 + 8 = 0 $$
$$ \ Rightarrow -4I_2 + I_1 + 8 = 0 $$
$ 4I_2 = I_1 + 8 $ Equation 2
Step 4- Нахождение токов сетки I 1 и I 2 путем решения уравнения 1 и уравнения 2.
Левая часть уравнения 1 и уравнения 2 одинаковы. Следовательно, приравняйте члены в правой части уравнения 1 и уравнения 2, чтобы найти значение I 1 .
$$ 6I_1 - 8 = I_1 + 8 $$
$$ \ Rightarrow 5I_1 = 16 $$
$$ \ Rightarrow I_1 = \ frac {16} {5} A $$
Подставьте значение I 1 в уравнение 2.
$$ 4I_2 = \ frac {16} {5} + 8 $$
$$ \ Rightarrow 4I_2 = \ frac {56} {5} $$
$$ \ Rightarrow I_2 = \ frac {14} {5} A $$
Итак, мы получили сеточные токи I 1 и I 2 как $ \ mathbf {\ frac {16} {5}} $A и $ \ mathbf {\ frac {14} {5}} $ A соответственно.
Step 5- Ток, протекающий через резистор 30 Ом, представляет собой не что иное, как ток сетки I 2, и он равен $ \ frac {14} {5} $ A. Теперь мы можем найти напряжение на резисторе 30 Ом, используя закон Ома.
$$ V_ {30 \ Omega} = I_2 R $$
Подставьте значения I 2 и R в приведенное выше уравнение.
$$ V_ {30 \ Omega} = \ lgroup \ frac {14} {5} \ rgroup 30 $$
$$ \ Rightarrow V_ {30 \ Omega} = 84V $$
Следовательно, напряжение на резисторе 30 Ом данной цепи равно 84 V.
Note 1- Из приведенного выше примера мы можем сделать вывод, что нам нужно решить уравнения m сеток, если электрическая цепь имеет m сеток. Вот почему мы можем выбрать анализ Mesh, когда число ячеек меньше, чем количество основных узлов (за исключением опорного узла) любой электрической цепи.
Note 2 - Можно выбрать либо анализ или анализ Nodal сетки, когда количество ячеек равно числу основных узлов (за исключением опорного узла) в любой электрической цепи.