Теория сетей - Теорема суперпозиции
Superposition theoremоснован на концепции линейности между реакцией и возбуждением электрической цепи. В нем говорится, что отклик в конкретной ветви линейной цепи, когда несколько независимых источников действуют одновременно, эквивалентен сумме откликов от каждого независимого источника, действующего одновременно.
В этом методе мы будем рассматривать только one independent sourceвовремя. Итак, мы должны исключить из схемы оставшиеся независимые источники. Мы можем исключить источники напряжения, закоротив их два вывода, и, аналогично, источники тока, открыв их два вывода.
Поэтому нам нужно найти ответ в конкретной ветке ‘n’ timesесли есть n независимых источников. Отклик в конкретной ветви может быть либо током, протекающим через эту ветвь, либо напряжением в этой ветви.
Процедура теоремы суперпозиции
Выполните следующие шаги, чтобы найти ответ в конкретной ветви, используя теорему суперпозиции.
Step 1 - Найдите ответ в конкретной ветке, рассмотрев один независимый источник и исключив остальные независимые источники, присутствующие в сети.
Step 2 - Повторите шаг 1 для всех независимых источников, присутствующих в сети.
Step 3 - Добавьте все ответы, чтобы получить общий ответ в конкретной ветви, когда в сети присутствуют все независимые источники.
пример
Найдите ток, протекающий через резистор 20 Ом следующей цепи, используя superposition theorem.
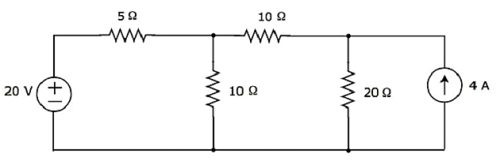
Step 1 - Давайте найдем ток, протекающий через резистор 20 Ом, рассматривая только 20 V voltage source. В этом случае мы можем устранить источник тока 4 А, замкнув его. Модифицированная принципиальная схема показана на следующем рисунке.

В приведенной выше схеме есть только один главный узел, кроме заземления. Итак, мы можем использоватьnodal analysisметод. Напряжение узла V 1 обозначено на следующем рисунке. Здесь V 1 - напряжение от узла 1 относительно земли.
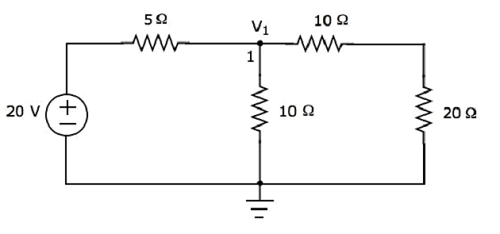
В nodal equation в узле 1
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$
$$ \ Rightarrow \ frac {6V_1 - 120 + 3V_1 + V_1} {30} = 0 $$
$$ \ Rightarrow 10V_1 = 120 $$
$$ \ Rightarrow V_1 = 12V $$
В current flowing through 20 Ω resistor можно найти, выполнив следующее упрощение.
$$ I_1 = \ frac {V_1} {10 + 20} $$
Подставьте значение V 1 в приведенное выше уравнение.
$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0,4 A $$
Следовательно, ток, протекающий через резистор 20 Ом, равен 0.4 A, когда рассматривается только источник напряжения 20 В.
Step 2 - Давайте найдем ток, протекающий через резистор 20 Ом, рассматривая только 4 A current source. В этом случае мы можем исключить источник напряжения 20 В, замкнув его накоротко. Модифицированная принципиальная схема показана на следующем рисунке.
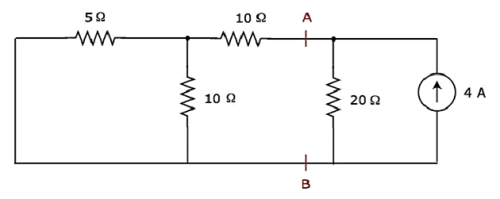
В приведенной выше схеме есть три резистора слева от клемм A и B. Мы можем заменить эти резисторы одним equivalent resistor. Здесь резисторы 5 Ом и 10 Ом подключены параллельно, и вся комбинация включена последовательно с резистором 10 Ом.
В equivalent resistance слева от терминалов A и B будет
$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
Упрощенная принципиальная схема показана на следующем рисунке.
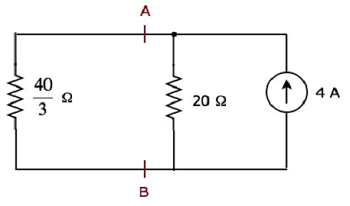
Мы можем найти ток, протекающий через резистор 20 Ом, используя current division principle.
$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Подставьте $ I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega $ и $ R_2 = 20 \ Omega $ в приведенное выше уравнение.
$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1,6 А $$
Следовательно, ток, протекающий через резистор 20 Ом, равен 1.6 A, когда рассматривается только источник тока 4 А.
Step 3 - Мы получим ток, протекающий через резистор 20 Ом данной цепи, выполнив addition of two currents что мы получили на шаге 1 и шаге 2. Математически это можно записать как
$$ I = I_1 + I_2 $$
Подставьте значения I 1 и I 2 в приведенное выше уравнение.
$$ I = 0,4 + 1,6 = 2 A $$
Следовательно, ток, протекающий через резистор 20 Ом данной цепи, равен 2 A.
Note - Мы не можем применить теорему суперпозиции напрямую, чтобы найти количество powerдоставляется на любой резистор, который присутствует в линейной цепи, просто путем добавления мощностей, передаваемых этому резистору из-за каждого независимого источника. Скорее, мы можем рассчитать либо полный ток, протекающий через резистор, либо напряжение на этом резисторе, используя теорему суперпозиции, и исходя из этого мы можем вычислить количество мощности, подаваемой на этот резистор, используя $ I ^ 2 R $ или $ \ frac {V ^ 2} {R} $.