Теорема о передаче максимальной мощности
Мощность, получаемая нагрузкой, является важным параметром в электрических и электронных приложениях. В цепях постоянного тока нагрузку можно представить резистором с сопротивлением R L Ом. Точно так же в цепях переменного тока мы можем представить это со сложной нагрузкой, имеющей импеданс Z L Ом.
Maximum power transfer theorem утверждает, что источник постоянного напряжения будет подавать максимальную мощность на резистор переменной нагрузки только тогда, когда сопротивление нагрузки равно сопротивлению источника.
Так же, Maximum power transfer theorem утверждает, что источник переменного напряжения будет обеспечивать максимальную мощность переменной комплексной нагрузки только в том случае, если полное сопротивление нагрузки равно комплексно-сопряженному сопротивлению источника.
В этой главе давайте обсудим теорему о максимальной передаче мощности для цепей постоянного тока.
Доказательство теоремы о максимальной передаче мощности
Замените любую двухконтактную линейную сеть или цепь слева от резистора переменной нагрузки, имеющего сопротивление R L Ом, эквивалентной схемой Тевенина. Мы знаем, что эквивалентная схема Тевенина напоминает практический источник напряжения.
Эта концепция проиллюстрирована на следующих рисунках.
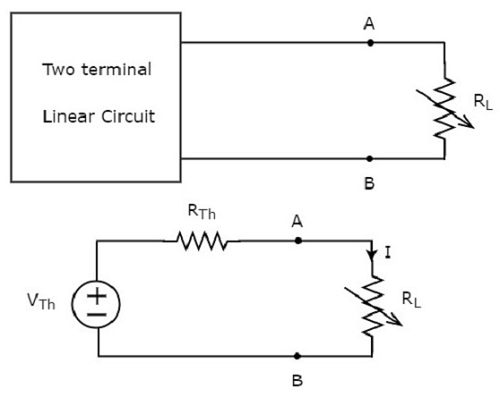
Количество мощности, рассеиваемой на нагрузочном резисторе, составляет
$$ P_L = I ^ 2 R_L $$
Подставьте $ I = \ frac {V_ {Th}} {R_ {Th} + R_L} $ в приведенное выше уравнение.
$$ P_L = \ lgroup \ frac {V_ {Th}} {(R_ {Th} + R_L)} \ rgroup ^ 2 R_L $$
$ \ Rightarrow P_L = {V_ {Th}} ^ 2 \ lbrace \ frac {R_L} {(R_ {Th} + R_L) ^ 2} \ rbrace $ Equation 1
Условие для максимальной передачи мощности
Для максимума или минимума первая производная будет равна нулю. Итак, продифференцируем уравнение 1 относительно R L и сделаем его равным нулю.
$$ \ frac {dP_L} {dR_L} = {V_ {Th}} ^ 2 \ lbrace \ frac {(R_ {Th} + R_L) ^ 2 \ times 1 - R_L \ times 2 (R_ {Th} + R_L) } {(R_ {Th} + R_L) ^ 4} \ rbrace = 0 $$
$$ \ Rightarrow (R_ {Th} + R_L) ^ 2 -2R_L (R_ {Th} + R_L) = 0 $$
$$ \ Rightarrow (R_ {Th} + R_L) (R_ {Th} + R_L - 2R_L) = 0 $$
$$ \ Rightarrow (R_ {Th} - R_L) = 0 $$
$$ \ Rightarrow R_ {Th} = R_L \: или \: R_L = R_ {Th} $$
Следовательно condition for maximum powerрассеяние по нагрузке составляет $ R_L = R_ {Th} $. Это означает, что если значение сопротивления нагрузки равно значению сопротивления источника, то есть сопротивлению Тевенина, то мощность, рассеиваемая на нагрузке, будет максимальной.
Значение максимальной передачи мощности
Подставьте $ R_L = R_ {Th} \: \ & \: P_L = P_ {L, Max} $ в уравнение 1.
$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {(R_ {Th} + R_ {Th}) ^ 2} \ rbrace $$
$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {4 {R_ {Th}} ^ 2} \ rbrace $$
$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {L}}, \: поскольку \: R_ {L} = R_ {Th} $$
Следовательно maximum amount of power передается в нагрузку
$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4R_ {L}} = \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} $$
Эффективность передачи максимальной мощности
Мы можем рассчитать эффективность передачи максимальной мощности, $ \ eta_ {Max} $, используя следующую формулу.
$ \ eta_ {Max} = \ frac {P_ {L, Max}} {P_S} $ Equation 2
Где,
$ P_ {L, Max} $ - максимальное количество мощности, передаваемой нагрузке.
$ P_S $ - количество энергии, генерируемой источником.
В amount of power generated по источнику
$$ P_S = I ^ 2 R_ {Th} + I ^ 2 R_L $$
$$ \ Rightarrow P_S = 2 I ^ 2 R_ {Th}, \: поскольку \: R_ {L} = R_ {Th} $$
Подставьте $ I = \ frac {V_ {Th}} {2 R_ {Th}} $ в приведенное выше уравнение.
$$ P_S = 2 \ lgroup \ frac {V_ {Th}} {2 R_ {Th}} \ rgroup ^ 2 R_ {Th} $$
$$ \ Rightarrow P_S = 2 \ lgroup \ frac {{V_ {Th}} ^ 2} {4 {R_ {Th}} ^ 2} \ rgroup R_ {Th} $$
$$ \ Rightarrow P_S = \ frac {{V_ {Th}} ^ 2} {2 R_ {Th}} $$
Подставьте значения $ P_ {L, Max} $ и $ P_S $ в уравнение 2.
$$ \ eta_ {Max} = \ frac {\ lgroup \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} \ rgroup} {\ lgroup \ frac {{V_ {Th}} ^ 2} { 2R_ {Th}} \ rgroup} $$
$$ \ Rightarrow \ eta_ {Max} = \ frac {1} {2} $$
Мы можем представить эффективность передачи максимальной мощности в виде percentage следующим образом -
$$ \% \ eta_ {Макс} = \ eta_ {Макс} \ times 100 \% $$
$$ \ Rightarrow \% \ eta_ {Max} = \ lgroup \ frac {1} {2} \ rgroup \ times 100 \% $$
$$ \ Rightarrow \% \ eta_ {Max} = 50 \% $$
Следовательно, эффективность передачи максимальной мощности равна 50 %.
пример
Найди maximum powerкоторый может подаваться на нагрузочный резистор R L схемы, показанной на следующем рисунке.
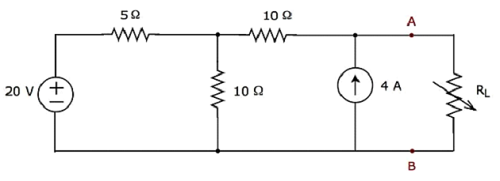
Step 1- В главе «Теорема Тевенина» мы рассчитали эквивалентную схему Тевенина для левой стороны клемм A и B. Теперь мы можем использовать эту схему. Это показано на следующем рисунке.
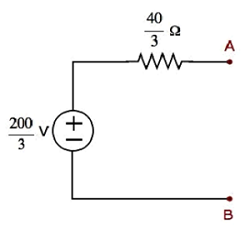
Здесь напряжение Тевенина $ V_ {Th} = \ frac {200} {3} V $ и сопротивление Тевенина $ R_ {Th} = \ frac {40} {3} \ Omega $
Step 2- Замените часть цепи, которая находится слева от клемм A и B данной цепи, на приведенную выше эквивалентную схему Тевенина. Результирующая принципиальная схема показана на следующем рисунке.

Step 3- Мы можем найти максимальную мощность, которая будет подаваться на нагрузочный резистор, R L , используя следующую формулу.
$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
Замените $ V_ {Th} = \ frac {200} {3} V $ и $ R_ {Th} = \ frac {40} {3} \ Omega $ в приведенной выше формуле.
$$ P_ {L, Max} = \ frac {\ lgroup \ frac {200} {3} \ rgroup ^ 2} {4 \ lgroup \ frac {40} {3} \ rgroup} $$
$$ P_ {L, Max} = \ frac {250} {3} W $$
Следовательно maximum power который будет доставлен на нагрузочный резистор RL данной схемы $ \ mathbf {\ frac {250} {3}} $ W