Теория сети - узловой анализ
Есть два основных метода, которые используются для решения любой электрической сети: Nodal analysis и Mesh analysis. В этой главе давайте обсудимNodal analysis метод.
В узловом анализе мы будем рассматривать узловые напряжения по отношению к земле. Следовательно, узловой анализ также называютNode-voltage method.
Процедура узлового анализа
Выполните эти шаги при решении любой электрической сети или цепи с помощью узлового анализа.
Step 1 - Определите principal nodes и выберите один из них как reference node. Мы будем рассматривать этот опорный узел как Землю.
Step 2 - Обозначьте node voltages по отношению к земле от всех основных узлов, за исключением опорного узла.
Step 3 - написать nodal equationsна всех основных узлах, кроме ссылочного. Узловое уравнение получается применением сначала KCL, а затем закона Ома.
Step 4 - Решите узловые уравнения, полученные на шаге 3, чтобы получить узловые напряжения.
Теперь мы можем найти ток, протекающий через любой элемент, и напряжение на любом элементе, который присутствует в данной сети, используя узловые напряжения.
пример
Найдите ток, протекающий через резистор 20 Ом следующей цепи, используя Nodal analysis.
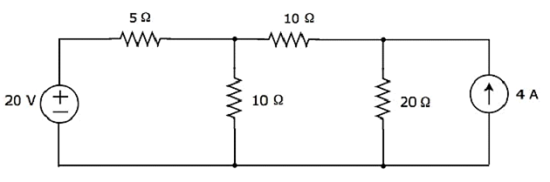
Step 1 - Есть three principle nodesв приведенной выше схеме. Они обозначены цифрами 1, 2 и 3 на следующем рисунке.
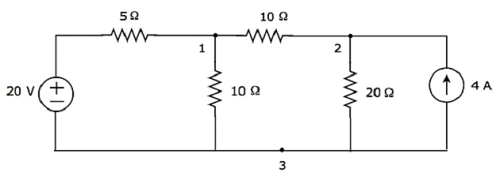
На приведенном выше рисунке рассмотрим node 3 как опорный узел (Земля).
Step 2- Напряжения в узлах V 1 и V 2 обозначены на следующем рисунке.
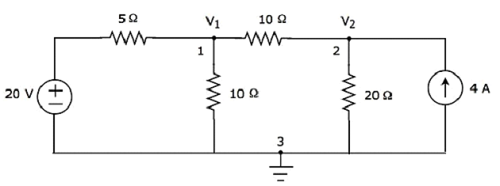
На приведенном выше рисунке V 1 - это напряжение от узла 1 относительно земли, а V 2 - это напряжение от узла 2 относительно земли.
Step 3 - В этом случае мы получим two nodal equations, поскольку есть два основных узла, 1 и 2, кроме Ground. Когда мы пишем узловые уравнения в узле, предположим, что все токи уходят из узла, для которого направление тока не указано, а напряжение этого узла больше, чем напряжения других узлов в цепи.
В nodal equation в узле 1
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow \ frac {2 V_1 - 40 + V_1 + V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow 4V_1 - 40 - V_2 = 0 $$
$ \ Rightarrow V_2 = 4V_1 - 40 $ Equation 1
В nodal equation в узле 2
$$ - 4 + \ frac {V_2} {20} + \ frac {V_2 - V_1} {10} = 0 $$
$$ \ Rightarrow \ frac {-80 + V_2 + 2V_2 - 2V_2} {20} = 0 $$
$ \ Rightarrow 3V_2 - 2V_1 = 80 $ Equation 2
Step 4- Определение узловых напряжений, V 1 и V 2, путем решения уравнения 1 и уравнения 2.
Подставьте уравнение 1 в уравнение 2.
$$ 3 (4 V_1 - 40) - 2 V_1 = 80 $$
$$ \ Rightarrow 12 V_1 - 120 - 2V_1 = 80 $$
$$ \ Rightarrow 10 V_1 = 200 $$
$$ \ Rightarrow V_1 = 20V $$
Подставьте V 1 = 20 В в уравнение 1.
$$ V_2 = 4 (20) - 40 $$
$$ \ Rightarrow V_2 = 40V $$
Итак, мы получили узловые напряжения V 1 и V 2 как20 V и 40 V соответственно.
Step 5- Напряжение на резисторе 20 Ом представляет собой не что иное, как напряжение узла V 2, и оно равно 40 В. Теперь мы можем найти ток, протекающий через резистор 20 Ом, используя закон Ома.
$$ I_ {20 \ Omega} = \ frac {V_2} {R} $$
Подставьте значения V 2 и R в приведенное выше уравнение.
$$ I_ {20 \ Omega} = \ frac {40} {20} $$
$$ \ Rightarrow I_ {20 \ Omega} = 2A $$
Следовательно, ток, протекающий через резистор 20 Ом данной цепи, равен 2 A.
Note- Из приведенного выше примера, мы можем сделать вывод, что мы должны решить «п» узловых уравнений, если электрическая цепь имеет «п» основные узлы (за исключением опорного узла). Следовательно, мы можем выбрать узловой анализ, когдаnumber of principal nodes (За исключением опорного узла) меньше, чем число ячеек любой электрической цепи.