Теория сети - параллельный резонанс
В предыдущей главе мы обсуждали важность последовательного резонанса. Теперь давайте обсудим параллельный резонанс в цепях RLC.
Схема параллельного резонанса
Если резонанс возникает в параллельном контуре RLC, то он называется Parallel Resonance. Рассмотрим следующееparallel RLC circuit, который представлен в векторном домене.
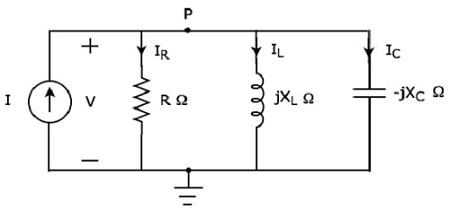
Здесь пассивные элементы, такие как резистор, катушка индуктивности и конденсатор, подключены параллельно. Вся эта комбинация находится вparallel с входным источником синусоидального тока.
Написать nodal equation в узле П.
$$ - I + I_R + I_L + I_C = 0 $$
$$ \ Rightarrow - I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0 $$
$$ \ Rightarrow I = \ frac {V} {R} - \ frac {jV} {X_L} + \ frac {jV} {X_C} $$
$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup] $Equation 1
Вышеприведенное уравнение имеет вид I = VY.
Следовательно admittance Y параллельной цепи RLC будет
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Параметры и электрические величины при резонансе
Теперь поочередно выведем значения параметров и электрических величин при резонансе параллельной RLC-цепи.
Резонансная частота
Мы знаем, что resonant frequency, fr- частота, при которой возникает резонанс. В параллельной цепи RLC возникает резонанс, когда мнимый член полной проводимости Y равен нулю. т.е. значение $ \ frac {1} {X_C} - \ frac {1} {X_L} $ должно быть равно нулю
$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$
$$ \ Rightarrow X_L = X_C $$
Вышеупомянутое условие резонанса такое же, как и для последовательной цепи RLC. Так чтоresonant frequency, fr будет одинаковым как в последовательной цепи RLC, так и в параллельной цепи RLC.
Следовательно resonant frequency, fr параллельной цепи RLC
$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$
Где,
- L - индуктивность катушки индуктивности.
- C - емкость конденсатора.
В resonant frequency, fr параллельной цепи RLC зависит только от индуктивности L и емкость C. Но это не зависит от сопротивленияR.
Прием
Мы получили admittance Y параллельной цепи RLC как
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Подставьте $ X_L = X_C $ в приведенное выше уравнение.
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_C} \ rgroup $$
$$ \ Rightarrow Y = \ frac {1} {R} + j (0) $$
$$ \ Rightarrow Y = \ frac {1} {R} $$
В резонансе admittance, Y параллельной цепи RLC равно сопротивлению, обратному сопротивлению R. т.е. $ \ mathbf {\ mathit {Y = \ frac {1} {R}}} $
Напряжение на каждом элементе
Заменить, $ \ frac {1} {X_C} - \ frac {1} {X_L} = 0 $ в уравнении 1
$$ I = V [\ frac {1} {R} + j (0)] $$
$$ \ Rightarrow I = \ frac {V} {R} $$
$$ \ Rightarrow V = IR $$
Следовательно voltage на всех элементах параллельной цепи RLC в резонансе V = IR.
В резонансе проводимость параллельной цепи RLC достигает минимального значения. Следовательно,maximum voltage присутствует на каждом элементе этой цепи в резонансе.
Ток, протекающий через резистор
Ток, протекающий через резистор, равен
$$ I_R = \ frac {V} {R} $$
Подставьте значение V в приведенном выше уравнении.
$$ I_R = \ frac {IR} {R} $$
$$ \ Rightarrow I_R = I $$
Следовательно current flowing through resistor при резонансе - $ \ mathbf {\ mathit {I_R = I}} $.
Ток, протекающий через индуктор
Ток, протекающий через катушку индуктивности, равен
$$ I_L = \ frac {V} {j X_L} $$
Подставьте значение V в приведенном выше уравнении.
$$ I_L = \ frac {IR} {j X_L} $$
$$ \ Rightarrow I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I $$
$$ \ Rightarrow I_L = -jQI $$
Следовательно current flowing through inductor при резонансе $ I_L = -jQI $.
Так что magnitude тока, протекающего через катушку индуктивности при резонансе, будет
$$ | I_L | = QI $$
Где, Q - Quality factor и его значение равно $ \ frac {R} {X_L} $
Ток, протекающий через конденсатор
Ток, протекающий через конденсатор, равен
$$ I_C = \ frac {V} {- j X_C} $$
Подставьте значение V в приведенном выше уравнении.
$$ I_C = \ frac {IR} {- j X_C} $$
$$ \ Rightarrow I_C = j \ lgroup \ frac {R} {X_C} \ rgroup I $$
$$ \ Rightarrow I_C = jQI $$
Следовательно current flowing through capacitor при резонансе $ I_C = jQI $
Так что magnitude тока, протекающего через конденсатор при резонансе, будет
$$ | I_C | = QI $$
Где, Q - Quality factor и его значение равно $ \ frac {R} {X_C} $
Note - Параллельный резонансный контур RLC называется current magnificationцепь. Так, величина тока , протекающего через катушку индуктивности и конденсатора равна Q раз входной синусоидальный ток I .