Сетевая теория - реакция цепей переменного тока

В предыдущей главе мы обсудили переходную характеристику и реакцию в установившемся режиме цепи постоянного тока. В этой главе давайте обсудимresponse of AC circuit. Понятия как переходной характеристики, так и реакции в установившемся режиме, которые мы обсуждали в предыдущей главе, также будут полезны здесь.

Поиск отклика цепи последовательного RL

Рассмотрим следующее series RL circuit диаграмма.

В приведенной выше схеме switch хранился openдо t = 0 и закрылся при t = 0 . Таким образом, источник переменного напряжения, имеющий пиковое напряжение V _м вольт, до этого момента не подключен к последовательной цепи RL. Следовательно, естьno initial current протекает через индуктор.

Принципиальная схема, когда switch в closed положение, показано на следующем рисунке.

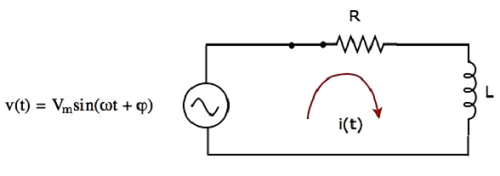
Теперь ток i (t) протекает по всей цепи, поскольку источник переменного напряжения, имеющий пиковое напряжение V _м вольт, подключен к последовательной цепи RL.

Мы знаем, что ток i (t), протекающий по вышеуказанной цепи, будет иметь два члена, один из которых представляет переходную часть, а другой - устойчивое состояние.

Математически это можно представить как

$ i (t) = i_ {Tr} (t) + i_ {ss} (t) $Equation 1

Где,

$ i_ {Tr} (t) $ - это переходная характеристика тока, протекающего по цепи.
$ i_ {ss} (t) $ - это установившаяся характеристика тока, протекающего по цепи.

В предыдущей главе мы получили переходную характеристику тока, протекающего по последовательной цепи RL. Он имеет вид $ Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $.

Подставьте $ i_ {Tr} (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $ в уравнение 1.

$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + i_ {ss} (t) $Equation 2

Расчет установившегося тока

Если синусоидальный сигнал подается в качестве входа в линейную электрическую цепь, то он дает выход установившегося состояния, который также является sinusoidal signal. И входные, и выходные синусоидальные сигналы будут иметь одинаковую частоту, но разные амплитуды и фазовые углы.

Мы можем рассчитать установившийся отклик электрической цепи, когда она возбуждается источником синусоидального напряжения, используя Laplace Transform approach.

Принципиальная схема s-домена, когда switch в closed положение, показано на следующем рисунке.

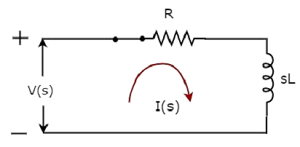
В приведенной выше схеме все величины и параметры представлены в s-domain. Это преобразования Лапласа величин и параметров во временной области.

В Transfer function приведенной выше схемы

$$ H (s) = \ frac {I (s)} {V (s)} $$

$$ \ Rightarrow H (s) = \ frac {1} {Z (s)} $$

$$ \ Rightarrow H (s) = \ frac {1} {R + sL} $$

Подставьте $ s = j \ omega $ в приведенное выше уравнение.

$$ H (j \ omega) = \ frac {1} {R + j \ omega L} $$

Magnitude of $ \ mathbf {\ mathit {H (j \ omega)}} $ - это

$$ | H (j \ omega) | = \ frac {1} {\ sqrt {R ^ 2 + {\ omega} ^ 2} L ^ 2} $$

Phase angle of $ \ mathbf {\ mathit {H (j \ omega)}} $ - это

$$ \ angle H (j \ omega) = -tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup $$

Мы получим steady state current $ i_ {ss} (t) $, выполнив следующие два шага:

Умножьте пиковое напряжение входного синусоидального напряжения на величину $ H (j \ omega) $.
Сложите фазовые углы входного синусоидального напряжения и $ H (j \ omega) $.

В steady state current $ i_ {ss} (t) $ будет

$$ i_ {ss} (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

Подставьте значение $ i_ {ss} (t) $ в уравнение 2.

$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} грех \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 3

Мы знаем, что в цепи нет начального тока. Следовательно, подставьте t = 0 & i (t) = 0 в уравнение 3, чтобы найти значение константы K.

$$ 0 = Ke ^ {- \ lgroup \ frac {0} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ омега (0) + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

$$ \ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ омега L} {R} \ rgroup \ rgroup $$

$$ \ Rightarrow K = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

Подставьте значение K в уравнение 3.

$ i (t) = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2 }} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 4

Уравнение 4 представляет ток, протекающий по последовательной цепи RL, когда он возбуждается источником синусоидального напряжения. Он состоит из двух сроков. Первый и второй члены представляют собой переходную характеристику и реакцию установившегося состояния тока соответственно.

Мы можем neglect the first termуравнения 4, потому что его значение будет намного меньше единицы. Таким образом, результирующий ток, протекающий по цепи, будет

$$ i (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ гидроразрыв {\ omega L} {R} \ rgroup \ rgroup $$

Он содержит только steady state term. Следовательно, мы можем найти только установившуюся характеристику цепей переменного тока и пренебречь ее переходной характеристикой.