Теория сети - топология сети
Топология сети - это графическое представление электрических цепей. Это полезно для анализа сложных электрических цепей путем преобразования их в сетевые графы. Топология сети также называетсяGraph theory.
Базовая терминология сетевой топологии
Теперь давайте обсудим основную терминологию, используемую в этой топологии сети.
График
Сетевой граф просто называется graph. Он состоит из набора узлов, соединенных ветвями. В графах узел - это общая точка двух или более ветвей. Иногда к узлу может подключаться только одна ветвь. Ветвь - это отрезок линии, соединяющий два узла.
Любую электрическую схему или сеть можно превратить в ее эквивалент graphпутем замены пассивных элементов и источников напряжения на короткие замыкания и источников тока на разомкнутые цепи. Это означает, что отрезки линии на графике представляют ветви, соответствующие либо пассивным элементам, либо источникам напряжения электрической цепи.
пример
Рассмотрим следующие electric circuit.
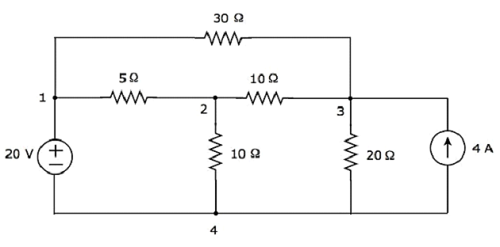
В приведенной выше схеме есть four principal nodes и они помечены цифрами 1, 2, 3 и 4. Есть seven branches в приведенной выше схеме, среди которой одна ветвь содержит источник напряжения 20 В, другая ветвь содержит источник тока 4 А, а остальные пять ветвей содержат резисторы с сопротивлением 30 Ом, 5 Ом, 10 Ом, 10 Ом и 20 Ом соответственно.
Эквивалент graph Соответствующая вышеуказанной электрической схеме показана на следующем рисунке.
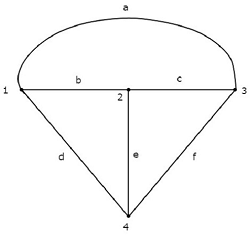
На приведенном выше графике есть four nodesи они помечены цифрами 1, 2, 3 и 4 соответственно. Они такие же, как у основных узлов в электрической цепи. Естьsix branches на приведенном выше графике, и они помечены как a, b, c, d, e и f соответственно.
В этом случае мы получили one branch less на графике, потому что источник тока 4 А выполнен в виде разомкнутой цепи, при этом электрическая цепь преобразуется в эквивалентный график.
Из этого примера мы можем сделать следующие выводы:
В number of nodes число присутствующих в графе будет равно количеству основных узлов, присутствующих в электрической цепи.
В number of branches число присутствующих на графике будет меньше или равно количеству ветвей, присутствующих в электрической цепи.
Типы графиков
Ниже приведены типы графиков -
- Связанный график
- Несвязанный граф
- Направленный график
- Ненаправленный граф
Теперь давайте обсудим эти графики один за другим.
Связанный график
Если между любым из двух узлов графа существует хотя бы одна ветвь, то она называется connected graph. Это означает, что каждый узел в связном графе будет иметь одну или несколько связанных с ним ветвей. Таким образом, ни один узел не будет представлен как изолированный или отдельный.
График, показанный в предыдущем примере, представляет собой connected graph. Здесь все узлы соединены тремя ветвями.
Несвязанный граф
Если существует хотя бы один узел в графе, который остается не связанным даже одной ветвью, то он называется unconnected graph. Итак, в несвязанном графе будет один или несколько изолированных узлов.
Рассмотрим график, показанный на следующем рисунке.
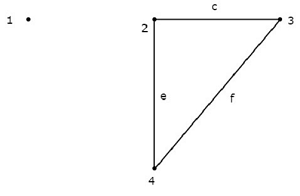
На этом графе узлы 2, 3 и 4 соединены двумя ветвями каждый. Но ни одна ветка не подключена кnode 1. Итак, узел 1 становитсяisolated node. Следовательно, приведенный выше график являетсяunconnected graph.
Направленный график
Если все ветви графа представлены стрелками, то этот граф называется directed graph. Эти стрелки указывают направление тока в каждой ветви. Следовательно, этот граф также называютoriented graph.
Рассмотрим график, показанный на следующем рисунке.
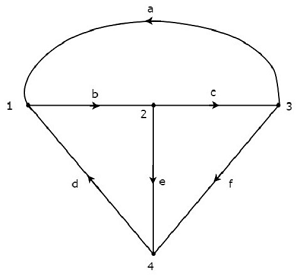
На приведенном выше графике направление тока показано стрелкой в каждой ветви. Следовательно, этоdirected graph.
Ненаправленный граф
Если ветви графа не представлены стрелками, то этот граф называется undirected graph. Поскольку нет направлений течения тока, этот график также называютunoriented graph.
График, показанный в первом примере этой главы, является unoriented graph, потому что на ветвях этого графа нет стрелок.
Подграф и его типы
Часть графа называется subgraph. Мы получаем подграфы, удаляя некоторые узлы и / или ветви данного графа. Таким образом, количество ветвей и / или узлов подграфа будет меньше, чем у исходного графа. Следовательно, мы можем заключить, что подграф - это подмножество графа.
Ниже приведены two types подграфов.
- Tree
- Co-Tree
Дерево
Дерево - это связный подграф данного графа, который содержит все узлы графа. Но в этом подграфе не должно быть никакого цикла. Ветви дерева называютсяtwigs.
Рассмотрим следующее connected subgraph графика, который показан в Примере в начале этой главы.
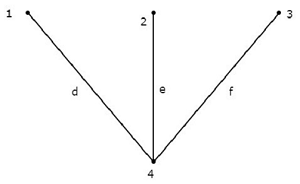
Этот связный подграф содержит все четыре узла данного графа, и в нем нет цикла. Следовательно, этоTree.
Это Дерево имеет только три ветви из шести ветвей данного графа. Потому что, если мы рассмотрим хотя бы одну ветвь остальных ветвей графа, то в вышеупомянутом связном подграфе будет петля. Тогда результирующий связный подграф не будет деревом.
Из приведенного выше Дерева мы можем сделать вывод, что number of branches которые присутствуют в дереве, должны быть равны n - 1 где n - количество узлов данного графа.
Co-Tree
Совместное дерево - это подграф, который образован ветвями, которые удаляются при формировании Дерева. Следовательно, он называетсяComplementдерева. Для каждого Дерева будет соответствующее Совместное Древо, и его ветви называютсяlinksили аккорды. Как правило, ссылки представлены пунктирными линиями.
В Co-Tree соответствующее приведенному выше дереву показано на следующем рисунке.
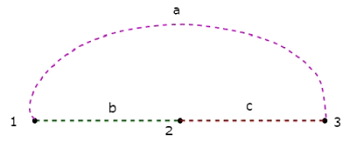
Это совместное дерево имеет только три узла вместо четырех узлов данного графа, потому что узел 4 изолирован от указанного выше совместного дерева. Следовательно, Co-Tree не обязательно должен быть связным подграфом. Это совместное дерево состоит из трех ветвей, образующих петлю.
В number of branchesкоторые присутствуют в совместном дереве, будут равны разнице между количеством ветвей данного графа и количеством веток. Математически это можно записать как
$$ l = b - (n - 1) $$
$$ l = b - n + 1 $$
Где,
- l количество ссылок.
- b количество ветвей в данном графе.
- n количество узлов в данном графе.
Если мы объединим Дерево и соответствующее ему Совместное дерево, то мы получим original graph как показано ниже.
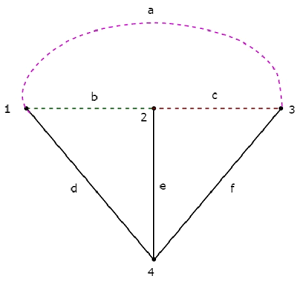
Ветви дерева d, e и f показаны сплошными линиями. Ветви совместного дерева a, b и c показаны пунктирными линиями.