Сетевая теория - реакция цепей постоянного тока
Если выходной сигнал электрической цепи для входа изменяется во времени, то он называется time response. Временной ответ состоит из следующих двух частей.
- Переходный ответ
- Устойчивый ответ
В этой главе давайте сначала обсудим эти два отклика, а затем рассмотрим эти два отклика в последовательной цепи RL, когда она возбуждается источником постоянного напряжения.
Переходный ответ
После подачи входного сигнала в электрическую цепь выходу требуется определенное время для достижения установившегося состояния. Таким образом, выход будет в переходном состоянии, пока не перейдет в устойчивое состояние. Следовательно, реакция электрической цепи во время переходного состояния известна какtransient response.
Переходная характеристика будет равна нулю для больших значений «t». В идеале это значение t должно быть бесконечным. Но практическиfive time constants достаточно.
Наличие или отсутствие переходных процессов
Переходные процессы возникают в ответе из-за sudden changeв источниках, приложенных к электрической цепи и / или в результате переключающего действия. Возможны два действия переключения. Это размыкающий переключатель и замыкающий переключатель.
В transient часть будет not presentв ответ на электрическую цепь или сеть, если она содержит только сопротивления. Потому какresistor имеет возможность регулировать любое количество напряжения и тока.
В transient part occurs в ответ на электрическую цепь или сеть из-за наличия элементов накопления энергии, таких как inductor and capacitor. Потому что они не могут мгновенно изменить энергию, хранящуюся в этих элементах.
Поведение индуктора
Предположим, что переключение происходит при t = 0.Inductor currentне изменяется мгновенно, когда происходит переключение. Это означает, что значение тока катушки индуктивности сразу после действия переключения будет таким же, как и непосредственно перед действием переключения.
Математически это можно представить как
$$ i_L (0 ^ +) = i_L (0 ^ -) $$
Конденсатор Поведение
В capacitor voltageне изменяется мгновенно, как ток индуктора, когда происходит переключение. Это означает, что значение напряжения конденсатора сразу после действия переключения будет таким же, как и непосредственно перед действием переключения.
Математически это можно представить как
$$ v_c (0 ^ +) = v_c (0 ^ -) $$
Устойчивый ответ
Часть временного отклика, которая остается даже после того, как переходный отклик стал нулевым значением для больших значений 't', известен как steady state response. Это означает, что в установившемся режиме в ответе не будет никаких переходных процессов.
Поведение индуктора
Если независимый источник подключен к электрической цепи или сети, имеющей один или несколько индукторов и резисторов (необязательно) в течение длительного времени, то эта электрическая цепь или сеть считается находящейся в устойчивом состоянии. Следовательно, энергия, запасенная в индукторе (ах) этой электрической цепи, является максимальной и постоянной.
Математически это можно представить как
$ W_L = \ frac {L {i_L} ^ 2} {2} = $ Максимум и константа
$ \ Rightarrow i_L = $ Максимум и константа
Следовательно, индуктор действует как constant current source в устойчивом состоянии.
Напряжение на катушке индуктивности будет
$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$
Итак, индуктор действует как short circuit в устойчивом состоянии.
Конденсатор Поведение
Если независимый источник подключен к электрической цепи или сети, имеющей один или несколько конденсаторов и резисторов (необязательно) в течение длительного времени, то говорят, что эта электрическая цепь или сеть находятся в устойчивом состоянии. Следовательно, энергия, запасенная в конденсаторе (ах) этой электрической цепи, является максимальной и постоянной.
Математически это можно представить как
$ W_c = \ frac {C {v_c} ^ 2} {2} = $ Максимум и константа
$ \ Rightarrow v_c = $ Максимум и константа
Следовательно, конденсатор действует как constant voltage source в устойчивом состоянии.
Ток, протекающий через конденсатор, будет
$$ i_c = C \ frac {dv_c} {dt} = 0A $$
Итак, конденсатор действует как open circuit в устойчивом состоянии.
Поиск отклика цепи последовательного RL
Рассмотрим следующее series RL circuit диаграмма.
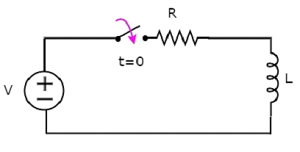
В приведенной выше схеме switch хранился openдо t = 0 и был замкнут при t = 0. Таким образом, источник постоянного напряжения, имеющий V вольт, до этого момента не подключен к последовательной цепи RL. Следовательно, естьno initial current протекает через индуктор.
Принципиальная схема, когда switch в closed положение показано на следующем рисунке.
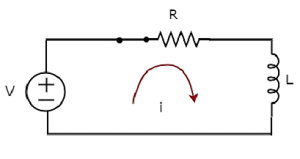
Теперь текущая i протекает по всей цепи, так как источник постоянного напряжения, имеющий V вольт подключен к последовательной цепи RL.
Теперь примените KVL вокруг петли.
$$ V = Ri + L \ frac {di} {dt} $$
$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1
Вышеупомянутое уравнение является дифференциальным уравнением первого порядка и имеет форму
$ \ frac {dy} {dt} + Py = Q $Equation 2
По comparing Уравнение 1 и уравнение 2, мы получим следующие соотношения.
$$ x = t $$
$$ y = i $$
$$ P = \ frac {R} {L} $$
$$ Q = \ frac {V} {L} $$
В solution уравнения 2 будет
$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3
Где, k постоянная.
Подставьте значения x, y, P и Q в уравнение 3.
$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $
$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4
Мы знаем, что в цепи нет начального тока. Следовательно, подставим, t = 0 и = 0 в уравнении 4, чтобы найти значение постоянной k.
$$ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $$
$$ 0 = \ frac {V} {R} + k (1) $$
$$ k = - \ frac {V} {R} $$
Подставим значение k в уравнение 4.
$$ i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
$$ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
Следовательно current протекает по цепи
$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5
Итак, реакция последовательной цепи RL, когда она возбуждается источником постоянного напряжения, имеет следующие два члена.
Первый член $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ соответствует transient response.
Второй член $ \ frac {V} {R} $ соответствует steady state response. Эти два ответа показаны на следующем рисунке.
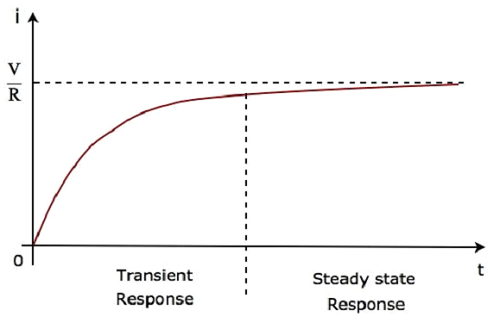
Мы можем переписать уравнение 5 следующим образом:
$ i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $
$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6
Где, τ это time constant и его значение равно $ \ frac {L} {R} $.
И уравнение 5, и уравнение 6 одинаковы. Но мы можем легко понять приведенную выше форму волны тока, протекающего по цепи из уравнения 6, подставив несколько значенийt например 0, τ, 2τ, 5τ и т. д.
В приведенной выше форме волны тока, протекающего по цепи, переходная характеристика будет представлять до пяти постоянных времени от нуля, тогда как реакция установившегося состояния будет представлена начиная с пяти постоянных времени.