Рассуждение - Часы
Стрелки часов могут иметь максимальный угол 180 ° между собой. Когда это происходит, обе руки представляют собой прямую линию.
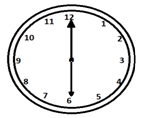
Стрелки часов делают прямые углы два раза в час, когда они находятся на расстоянии 15 минут друг от друга.
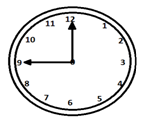
Две стрелки часов совпадают один раз в час.
Часы очень важны для каждого человека, чтобы планировать свои ежедневные задачи. Теория часов связана с повседневной жизнью.
Часы - это инструмент, который отображает время, разделяя его на часы, минуты и секунды.
Набирать номер
На круглом циферблате, пронумерованном от 1 до 12, указываются часы. Окружность циферблата разделена на 60 равных промежутков, которые называются минутными промежутками.
1 час = 60 минут
1 минута = 60 секунд и
1 час = 3600 секунд
Ухищрения
Между n и (n + 1) часами две стрелки часов совпадут на $ \ left (\ frac {60n} {11} \ right) $ min после n.
Между n и (n + 1) часами две стрелки часов будут взаимно образовывать прямой угол в $ \ left (5n \ pm 15 \ right) \ times \ frac {12} {11} $ min за n .
Между n и (n + 1) часами стрелки часов будут на прямой линии (не вместе) в точке
$ \ left (5n - 30 \ right) \ times \ frac {12} {11} $ мин за n, (когда n> 6)
$ \ left (5n + 30 \ right) \ times \ frac {12} {11} $ min после n (когда n <6)
Между n и (n + 1) часами стрелки часов находятся на расстоянии $ x $ min друг от друга в $ \ left (5n \ pm x \ right) \ times \ frac {12} {11} $ min после n. Знак «+» указывает на то, что впереди минутная стрелка, а знак «-» указывает на то, что впереди идет часовая стрелка.
Если минутная стрелка часов обгоняет часовую стрелку с интервалом $ x $ min правильного времени, то часы проигрывают или выигрывают на $ \ left (\ frac {720} {11} - x \ right) \ left (\ frac {60 \ times 24} {x} \ right) $ мин.
1 - В какое время между 7.15 и 8.15 стрелки часов будут совпадать?
Options -
A - 39 $ \ frac {5} {11} $
B - 39 $ \ frac {4} {11} $
C - 38 $ \ frac {5} {11} $
D - 39 $ \ frac {4} {11} $
Answer - А
Explanation -
$ \ frac {60 \ times n} {11} = \ frac {60} {11} \ times \ frac {29} {4} = 39 \ frac {5} {11} $
Где $ n = 7,15 = 7 \ frac {15} {60} = \ frac {29} {4} $
2 - В какое именно время, между 9 и 8 часами, обе стрелки будут под прямым углом друг к другу?
Options -
A - $ 65 \ frac {4} {11} $ и $ 32 \ frac {7} {11} $ мин. После 9
B - $ 65 \ frac {2} {11} $ и $ 32 \ frac {2} {11} $ мин. После 9
C - $ 65 \ frac {3} {11} $ и $ 32 \ frac {3} {11} $ мин после 9
D - $ 65 \ frac {1} {11} $ и $ 32 \ frac {1} {11} $ мин. После 9
Answer - А
Explanation -
$ \ left (5n \ pm 15 \ right) \ times \ frac {12} {11} = \ left (5 \ times9 \ pm 15 \ right) \ times \ frac {12} {11} $
$ = 65 \ frac {4} {11} $ и $ 32 \ frac {7} {11} $ мин. После 9
3 - Когда между 12 и 1 часами обе стрелки часов образуют прямую линию?
Options -
A- $ \ frac {360} {11} $ мин. последние 12
B- $ \ frac {355} {11} $ мин. последние 12
C- $ \ frac {340} {11} $ мин. последние 12
D- $ \ frac {345} {11} $ мин. последние 12
Answer - D
Explanation -
$ \ left (5n-30 \ right) \ times \ frac {12} {11} $ мин за n
$ \ left (6-30 \ right) \ times \ frac {12} {11} $ мин. последние 12
$ = \ frac {345} {11} $ мин. после 12 (поскольку n = 12)
4- Через сколько времени стрелки часов будут в 30 мин. расстояние между ними, когда они между 12 и 13 часами в понедельник?
Options -
A - $ \ frac {1080} {11} $ и $ \ frac {300} {11} $ мин. после 12
B - $ \ frac {1080} {12} $ и $ \ frac {360} {11} $ мин. после 12
C - $ \ frac {1080} {11} $ и $ \ frac {360} {11} $ мин. после 12
D - $ \ frac {1080} {12} $ и $ \ frac {300} {12} $ мин после 12
Answer - С
Explanation -
$ \ left (5n \ pm x \ right) \ times \ frac {12} {11} $
$ = \ left (5 \ times12 \ pm 30 \ right) \ times \ frac {12} {11} $
$ = \ frac {90 \ times12} {11} $ и $ \ frac {30 \ times12} {11} $ мин после 12 = $ \ frac {1080} {11} $ и $ \ frac {360} {11} $ мин после 12
5- Минутная стрелка часов обгоняет часовую стрелку с интервалом 61 мин. тогда часы отстают или отстают на сколько времени?
Options -
A - 104 $ \ frac {4} {671} $ мин.
B - 105 $ \ frac {1} {671} $ мин.
C - 104 $ \ frac {3} {671} $ мин.
D - 105 $ \ frac {4} {671} $ мин.
Answer - В
Explanation -
$ \ left (\ frac {720} {11} -61 \ right) \ times \ left (\ frac {60 \ times24} {61} \ right) $
$ = 105 \ frac {1} {671} $ мин.