Рассуждение - куб и кубоид
В настоящее время вопросы, основанные на «Кубах и кубоидах», задаются почти на всех конкурсных экзаменах. Эти проблемы очень часто встречаются на различных конкурсных экзаменах.
Описанные ниже методы просты, но элегантны. Они должны быть очень легкими для понимания, и после небольшой практики вы должны их освоить. Куб - это трехмерное твердое тело, имеющее 6 граней, 12 граней и углов. Все ребра куба равны, а все грани имеют квадратную форму. Это твердая фигура с шестью гранями; каждая грань, являющаяся квадратом, называетсяa cube. Если каждая из шести граней представляет собой прямоугольник, он называетсяcuboid. Кубоид также называютrectangular parallelepiped.
Вопросы, задаваемые по кубу и кубоиду, могут быть следующих типов.
Тип I
Дается несколько представлений всего куба, и вам нужно найти, какая часть куба находится точно под определенной частью.
Тип II
Дан раскрытый куб, и вы должны предсказать, как он будет выглядеть, когда он будет закрыт в куб.
Тип III
Куб нельзя было покрыть лаком или некоторые из его граней одним или разными цветами, а затем разрезать на определенное заданное количество одинаковых частей. Тогда вопрос формы - «сколько маленьких кубиков имеют 2 лица, покрытые лаком?» «Сколько маленьких кубиков покрыто лаком только на одной грани?» и т.п.
На экзамене появляются проблемы двух типов. Сначала вам дается несколько представлений оcomplete cube, и вы должны указать, какая часть куба находится точно под определенной частью. В другом типе вам даетсяopened-up cube, и вы должны предсказать, как он будет выглядеть, когда он будет замкнут в куб.
For Example -
Ниже показаны несколько граней куба -

Какое число окажется напротив 2?
A - 1
B - 6
C - 5
D - 4
Фундаментальный подход заключается в следующем -
Тип I
A fundamental rule: Opposite cannot be together;
Когда мы видим куб с видимыми нам только тремя гранями, мы никогда не сможем увидеть вместе две противоположные грани. Со всеми этими правилами мы можем легко решить тип проблемы, описанной выше. В приведенном выше вопросе, где мы должны найти противоположную грань определенного лица, мы можем исключить те лица, которые встречались вместе с X в любом виде. Таким образом, мы можем исключить любой другой выбор, и оставшееся будет нашим ответом.
На этом этапе вам следует еще раз просмотреть предыдущий абзац и убедиться, что вы поняли концепцию. После этого вы должны попытаться решить приведенный выше пример и посмотреть, сможете ли вы применить концепцию, описанную выше. Однако вы обнаружите, что не полностью поняли концепцию, нет проблем. Продолжайте читать этот раздел. Все станет ясно, когда вы закончите раздел. Зная вышеизложенное фундаментальное правило, вы можете решить вышеуказанный вопрос.
Для вопроса достаточно одного правила. После этого вы можете решить ее быстрее,three secondary rules.
Solution for above example -
В данном примере мы должны найти грань напротив 2. Теперь на первом рисунке 2 появляется вместе с 1 и 3. Это означает, что ни 1, ни 3 не могут быть противоположны 2. Это означает, что противоположно 1 мы можем имеет либо 4, либо 5, либо 6. Аналогично, напротив 3 мы можем иметь либо 4, либо 5, либо 6. Теперь посмотрите на вторую цифру. Здесь 3 и 1 встречаются вместе с 5. Это означает, что 5 не противоположно ни 3, ни 1. Таким образом, это означает, что либо 4, либо 6 противоположны 1, а другое - противоположно 3, поэтому 5 должно быть противоположным 2. Следовательно, 5 правильно ответ.
Некоторые более быстрые правила
Теперь вы, должно быть, поняли основной прием решения таких вопросов. Уловка состоит в том, что вы должны исключить те варианты, которые невозможны. Для этого вы воспользуетесь фундаментальным правилом, согласно которому, если две грани противоположны друг другу, их одновременное появление в одном виде куба невозможно. Однако в сегодняшних соревнованиях, требующих драгоценного времени, простая концепция не годится. Вы должны уметь быстро решать вопрос. Есть несколько второстепенных правил решения вопросов.
Rule I- Назовем ту цифру X, противоположность которой вам предстоит найти. Предположим, что в любом виде куба X появляется вместе с Y и Z. Вместе с третьей фигурой (скажем, A), тогда X будет напротив A.
Так, например, вам нужно найти лицо напротив 2 (это наш X). Теперь 2 появляется на одном рисунке вместе с 1 и 3. (Y и Z). Также 1 и 3 появляются вместе на еще одном рисунке вместе с 5. (То есть A). Следовательно, 2 должно быть напротив 5.
Rule II- Мы должны найти противоположную грань «Х». Предположим, что в любом из представлений куба X отображается с Y и Z. Теперь предположим, что Y и Z больше не отображаются вместе в каких-либо других представлениях, но они отображаются отдельно в двух или более разных представлениях. Тогда общей фигурой между двумя другими видами, на которой Y и Z появляются отдельно, будет цифра напротив X.
Rule III- Назовем фигуру X, противоположность которой вам предстоит найти. Теперь предположим, что X появляется в двух представлениях, и в этих двух представлениях с X видны четыре разные фигуры. Тогда единственная фигура, не видимая с X в этих двух представлениях, должна быть противоположна X.
Summary- Вы должны держать в уме основное правило, а затем применять три второстепенных правила для быстрых ответов. Весь подход можно резюмировать на следующей диаграмме.
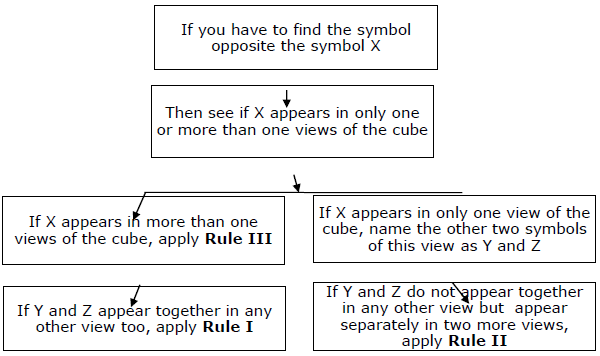
Тип II
В этом типе мы используем фундаментальное правило. Это правило помогает нам исключить те комбинации, в которых противоположные грани отображаются на одном экране. Таким образом, это приведет к исключению выбора при условии, что мы знаем, как определить, какое лицо будет напротив друг друга, глядя на «opened-up cube». Для этого есть очень простое правило, по которому вы можете сказать, посмотрев наopened-up cube, лица которых будут противоположны друг другу, просто глядя на него.
Правило приведено ниже;
Third is opposite rule -
Если вы хотите найти противоположное лицо лица (скажем, X), на рисунках I, II, III; дан раскрытый куб. Нам нужно найти, какие грани находятся напротив друг друга, когда куб замкнут.
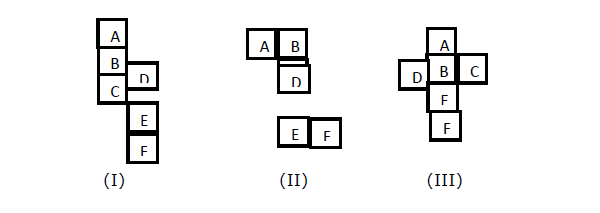
Explanation -
На рисунке (I) третье число для A - это C. Итак, A противоположно C. Итак, D и F будут противоположными. B и E будут противоположными.
На рисунке (II) B находится на третьем месте после D, поэтому B будет противоположным D. Аналогично, C будет противоположным E, а A будет противоположным F.
На рисунке (III) A противоположно E, B противоположно F. Следовательно, C противоположно D.
Steps to solve problem
Теперь мы можем решать вопросы такого типа. Мы знаем, как найти противоположное лицо, глядя наOpened-up cube. Мы также знаем, что в любом виде куба противоположные грани не могут быть вместе. Следовательно, сочетая два правила, мы можем легко решать проблемы.
Резюме
На этом обсуждение того, как решать вопросы типа II, завершено. Вы должны использовать третье правило, чтобы определить, какие грани противоположны друг другу. На следующей диаграмме представлена полная информация об этом подходе.

Тип III
Counting of Cubes (when a varnished solid cube is cut);
В предыдущем разделе мы обсудили проблему поиска противоположной грани куба. Существует еще один тип вопросов, связанных с кубиками, в которых большой куб, покрытый лаком разного цвета с разных сторон, разбивается на несколько кубиков меньшего размера, и вам нужно найти количество кубиков, у которых только одна сторона покрыта лаком или две стороны покрыты лаком.
Format of this problem -
Example -
Куб покрыт лаком трех цветов: зеленым, синим и красным на его сторонах, причем каждый цвет покрыт лаком на двух противоположных гранях куба. Теперь куб разбит на 64 кубика одинакового размера. Основываясь на этой информации, ответьте на следующие вопросы -
1. Сколько кубиков имеют две стороны, покрытые лаком, а остальные - без покрытия?
A - 18
B - 20
C - 22
D - 24
2. Сколько кубиков покрыто лаком только с одной стороны (только зеленым или синим цветом)
A - 4
B - 24
C - 16
D - 12
3. Сколько кубиков не покрыто лаком по бокам?
A - 0
B - 8
C - 12
D - 64