Năng khiếu - Hình học

Điểm

Một điểm là một vị trí chính xác

Phân đoạn dòng

Đường thẳng giữa hai điểm A và B gọi là đoạn thẳng AB. Một đoạn thẳng có hai điểm cuối.

cá đuối

Trên kéo dài đoạn thẳng AB không xác định theo một phương, ta được tia AB. Tia AB có một điểm cuối là A.

HÀNG

Đoạn thẳng AB kéo dài vô hạn về cả hai phương được gọi là đoạn thẳng AB.

Một dòng chứa vô số điểm.
Thông qua một số điểm đã cho, có thể vẽ ra nhiều đường thẳng.
Kẻ được một và chỉ một đường thẳng đi qua hai điểm A và B cho trước.
Hai đường thẳng gặp nhau tại một điểm.
Hai máy bay gặp nhau trên một đường thẳng.

Thẳng hàng

Trong hình đã cho, các điểm A, B, C thẳng hàng.

Dòng đồng thời

Ba hoặc nhiều đường thẳng cắt nhau tại cùng một điểm được gọi là các đường thẳng đồng quy.

Góc

Hai tia OA và OB có điểm cuối là O chung tạo thành góc AOB, viết là ∠AOB

Đo một góc

Lượng chuyển từ OA sang OB được gọi là số đo của ∠AOB viết là m (∠AOB).

Một góc 360 °

Nếu một tia OA bắt đầu từ vị trí ban đầu của nó OA, quay xung quanh O theo hướng ngược chiều kim đồng hồ và sau khi quay hoàn toàn quay trở lại vị trí ban đầu của nó, thì ta nói rằng nó đã quay 360. Phép quay hoàn chỉnh này được chia thành các phần bằng nhau 360 °. Sau đó, mỗi phần được gọi là 1 độ, viết là 1 °

1 ° = 60 phút, viết là 60 '

1 phút = 60 giây, được viết là 60 "

Các loại góc

Right angle - Góc có số đo là 90 ° được gọi là góc vuông.
Acute angle - Góc có số đo nhỏ hơn 90 ° được gọi là góc nhọn.
Obtuse angle - Góc có số đo lớn hơn 90 ° nhưng nhỏ hơn 180 ° được gọi là góc tù.
Straight angle - Góc có số đo là 180 ° được gọi là góc thẳng.
Reflex angle - Một góc có số đo lớn hơn 180 ° nhưng nhỏ hơn 360 °, được gọi là góc phản xạ.
Complete angle - Một góc có số đo là 360 ° được gọi là góc hoàn chỉnh.
Equal angle - Hai góc đã cho là bằng nhau, nếu chúng có cùng số đo.
Complementary angleHai góc được cho là bù nhau nếu tổng các số đo của chúng là 90. Ví dụ, các góc đo 65 ° và 25 ° là góc bù nhau.
Supplementary angle- Hai góc được cho là bổ sung nếu tổng các số đo của chúng là 180 °. Ví dụ, các thước đo góc 70 ° và 110 ° là bổ sung.
Adjacent angle- Hai góc được gọi là góc kề nhau nếu chúng có cùng đỉnh và một nhánh chung sao cho các nhánh không chung nằm về hai phía của nhánh dấu phẩy. Trong hình đã cho, ∠AOC và ∠BOC là góc kề nhau.

Kết quả quan trọng

Nếu một tia đứng trên một đoạn thẳng thì tổng của hai góc kề nhau tạo thành là 180 ° Trong hình đã cho, tia CP đứng trên đoạn thẳng AB.

∴ ∠ACD + ∠BCD = 180°.

Tổng của tất cả các góc tạo thành trên cùng một phía của một đoạn thẳng tại một điểm cho trước trên đoạn thẳng là 180 °. Trong hình đã cho, bốn góc được tạo thành ở cùng một phía của AOB.

∴ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180°.

Tổng của tất cả các góc xung quanh một điểm là 360 ° Trong hình đã cho, năm góc được tạo thành xung quanh một điểm O.

∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°.

Góc đối diện theo chiều dọc

Nếu hai đường thẳng A Band CD cắt nhau tại điểm O thì AOC, BOD và BOC, AOD là hai cặp góc đối đỉnh Góc đối đỉnh luôn bằng nhau.

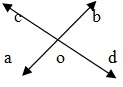
∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC

Những đường thẳng song song

Nếu hai đường thẳng nằm trong cùng một mặt phẳng và không cắt nhau khi sinh ra ở hai phía thì các đường thẳng đó được cho là song song và chúng ta viết, L || m.

Đường ngang cắt các đường song song

Cho hai đường thẳng song song AB và CD cắt bởi một đường thẳng EF. Sau đó

Góc tương ứng bằng

(∠1 = ∠5), (∠4= ∠8 ), (∠2 = ∠6) , (∠3 = ∠7)

Các góc nội tiếp xen kẽ bằng nhau.

(∠3 =∠5 )  and  (∠4 =∠6 )

Các góc nội thất có tính bổ sung

∠4+∠5 = 180° and ∠3 +∠6 = 180°.

Tam giác

Hình giới hạn bởi ba đoạn thẳng được gọi là hình tam giác. Trong hình đã cho, ta có ∆ABC; ∆ABC có ba đỉnh A, B, C. Trong có ba góc là ∠A, ∠B và ∠C. Nó có ba cạnh là AB, AC và BC.

Các loại hình tam giác

Một tam giác có tất cả các cạnh bằng nhau được gọi là tam giác đều.
Tam giác có hai cạnh bằng nhau được gọi là tam giác cân.
Một tam giác có tất cả các cạnh có độ dài khác nhau, được gọi là tam giác vô hướng.
Một tam giác có các góc bằng 90 ° được gọi là tam giác vuông.
Một tam giác có góc nằm giữa 90 ° và 180 ° được gọi là tam giác tù.
Mỗi tam giác có góc nhọn được gọi là tam giác nhọn.
Tổng tất cả các cạnh của một tam giác được gọi là chu vi của tam giác.
Tổng hai cạnh của một tam giác lớn hơn cạnh thứ ba.
Trong ABC vuông góc có ∠B = 90 °, ta có AC ² = AB ² + BC ² . Đây được gọi là Định lý Pythagoras.

Tứ giác

Hình được giới hạn bởi bốn đoạn thẳng được gọi là hình tứ giác. Tổng tất cả các góc của một tứ giác là 360 °.

Rectangle- Hình tứ giác được gọi là hình chữ nhật, nếu cạnh đối diện của nó bằng nhau và mỗi góc của nó bằng 90 °. Trong hình đã cho. ABCD là hình chữ nhật.
Square- Một tứ giác được gọi là hình vuông, nếu tất cả các cạnh của nó bằng nhau và mỗi góc của nó bằng 90 °. Trong hình đã cho. ABCD là hình vuông trong đó AB = BC = CD = DA.
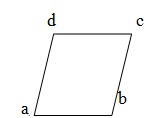
Parallelogram- Tứ giác được gọi là hình bình hành nếu các cạnh đối diện của nó song song. Trong hình đã cho. ABCD là hình bình hành trong đó AB = DC & AD = BC.
Rhombus- Hình bình hành có tất cả các cạnh bằng nhau được gọi là hình thoi. Trong hình đã cho. ABCD là hình thoi trong đó AB = BC = CD = DA, AB || DC và AD || BC.

Sự kiện quan trọng

Tứ giác là hình chữ nhật nếu các cạnh đối diện bằng nhau và các đường chéo của nó bằng nhau.
Một tứ giác là một hình vuông nếu tất cả các cạnh bằng nhau và đường chéo bằng nhau.
Tứ giác là một hình bình hành, nếu các cạnh đối diện bằng nhau.
Tứ giác là một hình bình hành nhưng không phải là một hình chữ nhật, nếu các cạnh đối diện bằng nhau nhưng các đường chéo không bằng nhau.
Một tứ giác là một hình thoi nhưng không phải là một hình vuông nếu tất cả các cạnh của chúng bằng nhau và các đường chéo không bằng nhau.

Kết quả về Tứ giác

Trong một hình bình hành, chúng ta có
1. Các cạnh đối diện bằng nhau.
2. Các góc đối diện bằng nhau.
3. Mỗi đường chéo chia đôi hình bình hành.
4. Các đường chéo của một hình bình hành cắt nhau.
Các đường chéo của một hình chữ nhật bằng nhau.
Các đường chéo của một hình thoi phân giác vuông góc với nhau.

Kết quả trên vòng kết nối

Đường vuông góc từ trung tâm đến một hợp âm chia đôi hợp âm.
Có một và chỉ một đường tròn đi qua ba điểm không thẳng hàng.
Góc trong nửa đường tròn là góc vuông.
Các góc đối của tứ giác nội tiếp là phụ nhau.
Góc trong cùng một đoạn của một đường tròn bằng nhau.
Tiếp tuyến tại một điểm bất kỳ của đường tròn vuông góc với bán kính qua tiếp điểm.
Hai tiếp tuyến của một đường tròn từ một điểm bên ngoài nó bằng nhau.
Nếu PT là tiếp tuyến của đường tròn và PAB là tiếp tuyến thì PA x PB = PT ²

Các ví dụ đã giải quyết