Chiều cao & Khoảng cách - Các ví dụ đã giải quyết

CÂU 1 - Từ một điểm cách chân tháp 375m, người ta quan sát đỉnh tháp ở góc nghiêng 45o, khi đó chiều cao (tính bằng mét) của tháp là?

A - 375

B - 450

C - 225

D - 250

Answer - A

Explanation

From the right angled triangle
Tan(45°)=  X/375
=> X = 375 m

Q 2 - Góc nâng của tháp tại điểm cách tháp 90 m là cot ^-1 (4/5). Khi đó chiều cao của tháp là

A - 45

B - 90

C - 112,5

D - 150

Answer - C

Explanation

Let cot^-1(4/5) = x 
=> cotx =  4/5   
=> tan(x) = 5/4   
From the right angled triangle
Tan(x) =  h/90 
=> h = 5/4*90 =112.5 m

Q 3 - Trên mặt bằng, góc nâng của đỉnh tháp là 30 °. Khi di chuyển gần hơn 20m thì góc nâng là 45 °. Khi đó chiều cao của tháp là

A - 10

B - √3

C - 10√3

D - 20√3

Answer - C

Explanation

Let h be the height of tower
From figure.
20 =h (  cot30 - cot60)	
20 =h (√3-1/√3) 
=> 20√3 = h (3-1) 
=> h=10√3.

Q 4 - Góc nâng của các đỉnh của hai tháp thẳng đứng khi nhìn từ điểm giữa của các đường nối chân tháp là 45 ° & 60 °. Tỷ lệ chiều cao của các tháp là

A - √3: 2

B - √3: 1

C - 2: √3

D - 2: 1

Answer - B

Explanation

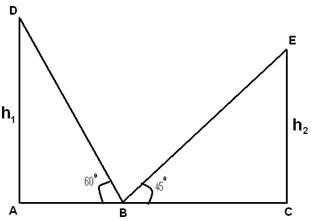
Tan(60)=h₁/AB
=> h1=√3AB
Tan(45)=h₁/BC
=> h2=BC
h1/ h2=√3/1
=> h1:h2=√3:1

Q 5 - Chiều cao của hai tháp là 90 mét và 45 mét. Đường thẳng hợp với đỉnh của chúng tạo với phương một góc 450 với phương ngang thì khoảng cách giữa hai tháp là

A - 22,5 m

B - 45 m

C - 60 m

D - 30 m

Answer - B

Explanation

Let the distance between the towers be X 
From the right angled triangle CFD 
Tan(45)=  (90-45)/X   
=> x=45 meters

Q 6 - Từ một điểm P trên mặt đất bằng phẳng, góc nâng của đỉnh tháp là 60 °. Nếu tháp cao 180 m thì khoảng cách của điểm P tính từ chân tháp là

A - 60√3

B - 40√3

C - 30√3

D - 20√3

Answer - A

Explanation

From ∠APB = 60° and AB = 180 m.
AB/AP= tan 60° =√3
AP=AB/√3 =180/√3=60√3

Q 7 - Đỉnh tháp cao 25 mét tạo với đáy cột điện một góc 450 và góc nâng 30 độ với đỉnh cột. Tìm chiều cao của cột điện.

A - 25√3

B - 25 ((√3-1) / √3)

C - 25 / √3

D - 25 ((1-√3) / √3)

Answer - B

Explanation

Let AB be the tower and CD be the electric pole. 
From the figure CA = DE
=> 25/(Tan(45))=(25-h)/(Tan(30))
=> 25  Tan(30) = 25-h
=> h=25-25Tan(30)
=25(1- Tan(30)) 
=25((√3-1)/√3)

CÂU 8 - Một quan sát viên cao 1,4 m cách tháp 10√3. Góc nâng từ mắt của người đó đến đỉnh tháp là 60 °. Chiều cao của tháp là

A - 12,4 m

B - 6,2 m

C - 11,4√3 m

D - 11,4 m

Answer - D

Explanation

Let AB be the observer and CD be the tower.
Then, CE = AB = 1.4 m,
 BE = AC = 10v3 m.
DE/BE=Tan (30) =1/√3
DE=10√3/√3=10
CD=CE+DE=1.4+10=11.4 m

Câu hỏi 9 - Một người đàn ông đang quan sát trên đỉnh tháp một chiếc thuyền đang tăng tốc rời khỏi tháp. Con thuyền tạo góc lõm 60 ° với mắt của người đàn ông khi ở khoảng cách 75 mét từ tháp. Sau 10 giây, góc lõm trở thành 45 °. Tốc độ gần đúng của thuyền là bao nhiêu, giả sử rằng nó đang chạy trong nước yên?

A - 54 kmph

B - 64 kmph

C - 24 kmph

D - 19,8 kmph

Answer - D

Explanation

Let AB be the tower and C and D be the positions of the boat.
Distance travelled by boat = CD
From the figure 75tan(60)=(75+CD)tan(45)
=>75√3 = 75+CD
=>CD =55 m
Speed = distance/time=55/10
=5.5 m/sec=19.8 kmph

Q 10 - Khoảng cách theo phương ngang giữa hai tháp là 90 m. Góc lõm của đỉnh thứ nhất khi nhìn từ đỉnh thứ hai cao 180 m là 450. Khi đó chiều cao của đỉnh thứ nhất là

A - 90√3 m

B - 45 m

C - 90 m

D - 150 m

Answer - C

Explanation