Sistem Kontrol - Aljabar Diagram Blok
Aljabar diagram blok tidak lain adalah aljabar yang terlibat dengan elemen-elemen dasar diagram blok. Aljabar ini berhubungan dengan representasi gambar dari persamaan aljabar.
Koneksi Dasar untuk Blok
Ada tiga tipe dasar koneksi antara dua blok.
Koneksi Seri
Koneksi seri juga disebut cascade connection. Pada gambar berikut, dua blok yang memiliki fungsi transfer $ G_1 (s) $ dan $ G_2 (s) $ dihubungkan secara seri.

Untuk kombinasi ini, kita akan mendapatkan output $ Y (s) $ as
$$ Y (s) = G_2 (s) Z (s) $$
Di mana, $ Z (s) = G_1 (s) X (s) $
$$ \ Rightarrow Y (s) = G_2 (s) [G_1 (s) X (s)] = G_1 (s) G_2 (s) X (s) $$
$$ \ Rightarrow Y (s) = \ lbrace G_1 (s) G_2 (s) \ rbrace X (s) $$
Bandingkan persamaan ini dengan bentuk standar persamaan keluaran, $ Y (s) = G (s) X (s) $. Dimana, $ G (s) = G_1 (s) G_2 (s) $.
Itu berarti kami dapat mewakili series connectiondari dua blok dengan satu blok. Fungsi transfer dari blok tunggal ini adalahproduct of the transfer functionsdari dua blok tersebut. Diagram blok ekuivalen ditunjukkan di bawah ini.
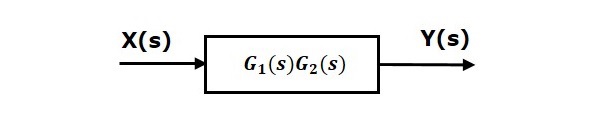
Demikian pula, Anda dapat merepresentasikan koneksi seri blok 'n' dengan satu blok. Fungsi transfer blok tunggal ini adalah hasil kali dari fungsi transfer dari semua blok 'n' tersebut.
Koneksi Paralel
Blok yang terhubung parallel akan memiliki same input. Pada gambar berikut, dua blok yang memiliki fungsi transfer $ G_1 (s) $ dan $ G_2 (s) $ dihubungkan secara paralel. Output dari kedua blok ini dihubungkan ke titik penjumlahan.

Untuk kombinasi ini, kita akan mendapatkan output $ Y (s) $ as
$$ Y (s) = Y_1 (s) + Y_2 (s) $$
Di mana, $ Y_1 (s) = G_1 (s) X (s) $ dan $ Y_2 (s) = G_2 (s) X (s) $
$$ \ Rightarrow Y (s) = G_1 (s) X (s) + G_2 (s) X (s) = \ lbrace G_1 (s) + G_2 (s) \ rbrace X (s) $$
Bandingkan persamaan ini dengan bentuk standar persamaan keluaran, $ Y (s) = G (s) X (s) $.
Di mana, $ G (s) = G_1 (s) + G_2 (s) $.
Itu berarti kami dapat mewakili parallel connectiondari dua blok dengan satu blok. Fungsi transfer dari blok tunggal ini adalahsum of the transfer functionsdari dua blok tersebut. Diagram blok ekuivalen ditunjukkan di bawah ini.

Demikian pula, Anda dapat merepresentasikan koneksi paralel dari blok 'n' dengan satu blok. Fungsi transfer blok tunggal ini adalah penjumlahan aljabar dari fungsi transfer dari semua blok 'n' tersebut.
Koneksi Umpan Balik
Seperti yang telah kita bahas di bab sebelumnya, ada dua jenis feedback- Umpan balik positif dan umpan balik negatif. Gambar berikut menunjukkan sistem kendali umpan balik negatif. Di sini, dua blok yang memiliki fungsi transfer $ G (s) $ dan $ H (s) $ membentuk loop tertutup.

Output dari titik penjumlahan adalah -
$$ E (s) = X (s) -H (s) Y (s) $$
Keluaran $ Y (s) $ adalah -
$$ Y (s) = E (s) G (s) $$
Gantikan nilai $ E (s) $ dalam persamaan di atas.
$$ Y (s) = \ kiri \ {X (s) -H (s) Y (s) \ rbrace G (s) \ right \} $$
$$ Y (s) \ kiri \ {1 + G (s) H (s) \ rbrace = X (s) G (s) \ kanan \} $$
$$ \ Rightarrow \ frac {Y (s)} {X (s)} = \ frac {G (s)} {1 + G (s) H (s)} $$
Oleh karena itu, fungsi transfer loop tertutup umpan balik negatif adalah $ \ frac {G (s)} {1 + G (s) H (s)} $
Ini berarti kami dapat mewakili koneksi umpan balik negatif dari dua blok dengan satu blok. Fungsi transfer dari blok tunggal ini adalah fungsi transfer loop tertutup dari umpan balik negatif. Diagram blok ekuivalen ditunjukkan di bawah ini.

Demikian pula, Anda dapat mewakili koneksi umpan balik positif dari dua blok dengan satu blok. Fungsi transfer dari blok tunggal ini adalah fungsi transfer loop tertutup dari umpan balik positif, yaitu $ \ frac {G (s)} {1-G (s) H (s)} $
Aljabar Diagram Blok untuk Menjumlahkan Poin
Ada dua kemungkinan untuk menggeser poin penjumlahan sehubungan dengan blok -
- Menggeser titik penjumlahan setelah blok
- Menggeser titik penjumlahan sebelum balok
Sekarang mari kita lihat pengaturan seperti apa yang perlu dilakukan dalam dua kasus di atas satu per satu.
Menggeser Titik Penjumlahan Setelah Balok
Perhatikan diagram blok yang ditunjukkan pada gambar berikut. Di sini, titik penjumlahan ada sebelum balok.

Titik penjumlahan memiliki dua input $ R (s) $ dan $ X (s) $. Outputnya adalah $ \ left \ {R (s) + X (s) \ right \} $.
Jadi, input ke blok $ G (s) $ adalah $ \ left \ {R (s) + X (s) \ right \} $ dan outputnya adalah -
$$ Y (s) = G (s) \ kiri \ {R (s) + X (s) \ kanan \} $$
$ \ Rightarrow Y (s) = G (s) R (s) + G (s) X (s) $ (Equation 1)
Sekarang, geser titik penjumlahan setelah balok. Diagram blok ini ditunjukkan pada gambar berikut.

Keluaran dari blok $ G $ adalah $ G (s) R (s) $.
Output dari titik penjumlahan adalah
$ Y (s) = G (s) R (s) + X (s) $ (Equation 2)
Bandingkan Persamaan 1 dan Persamaan 2.
Suku pertama $ 'G (s) R (s)' $ sama di kedua persamaan. Namun, ada perbedaan pada istilah kedua. Untuk mendapatkan suku kedua yang juga sama, kita membutuhkan satu blok lagi $ G $. Itu memiliki input $ X (s) $ dan output dari blok ini diberikan sebagai input ke titik penjumlahan alih-alih $ X (s) $. Diagram blok ini ditunjukkan pada gambar berikut.
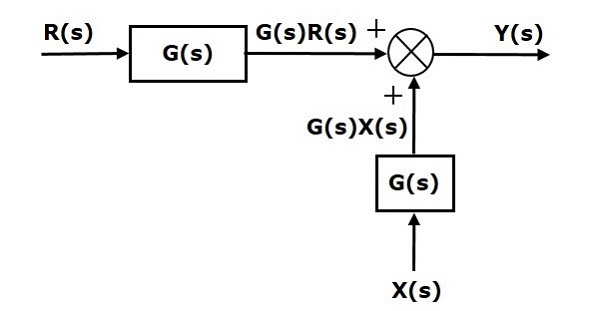
Menggeser Titik Penjumlahan Sebelum Balok
Perhatikan diagram blok yang ditunjukkan pada gambar berikut. Di sini, titik penjumlahan ada setelah balok.

Output dari diagram blok ini adalah -
$ Y (s) = G (s) R (s) + X (s) $ (Equation 3)
Sekarang, geser titik penjumlahan sebelum balok. Diagram blok ini ditunjukkan pada gambar berikut.

Output dari diagram blok ini adalah -
$ Y (S) = G (s) R (s) + G (s) X (s) $ (Equation 4)
Bandingkan Persamaan 3 dan Persamaan 4,
Suku pertama $ 'G (s) R (s)' $ sama di kedua persamaan. Namun, ada perbedaan pada istilah kedua. Untuk mendapatkan suku kedua yang juga sama, kita membutuhkan satu blok lagi $ \ frac {1} {G (s)} $. Itu memiliki input $ X (s) $ dan output dari blok ini diberikan sebagai input ke titik penjumlahan alih-alih $ X (s) $. Diagram blok ini ditunjukkan pada gambar berikut.

Aljabar Diagram Blok untuk Titik Lepas Landas
Ada dua kemungkinan untuk menggeser titik lepas landas sehubungan dengan blok -
- Menggeser titik lepas landas setelah blok
- Menggeser titik lepas landas sebelum blok
Sekarang mari kita lihat pengaturan seperti apa yang harus dilakukan dalam dua kasus di atas, satu per satu.
Menggeser Titik Lepas Setelah Blok
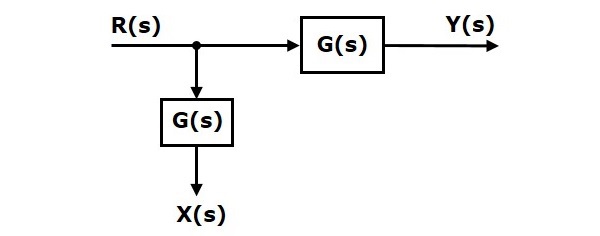
Perhatikan diagram blok yang ditunjukkan pada gambar berikut. Dalam hal ini, titik lepas landas ada sebelum blok.

Di sini, $ X (s) = R (s) $ dan $ Y (s) = G (s) R (s) $
Ketika Anda menggeser titik take-off setelah blok, output $ Y (s) $ akan sama. Namun, ada perbedaan dalam nilai $ X (s) $. Jadi, untuk mendapatkan nilai $ X (s) $ yang sama, kami memerlukan satu blok lagi $ \ frac {1} {G (s)} $. Itu memiliki masukan $ Y (s) $ dan keluarannya $ X (s) $. Diagram blok ini ditunjukkan pada gambar berikut.

Menggeser Titik Lepas Sebelum Blok
Perhatikan diagram blok yang ditunjukkan pada gambar berikut. Di sini, titik lepas landas ada setelah blok.

Di sini, $ X (s) = Y (s) = G (s) R (s) $
Ketika Anda menggeser titik take-off sebelum blok, output $ Y (s) $ akan sama. Namun, ada perbedaan dalam nilai $ X (s) $. Jadi, untuk mendapatkan nilai $ X (s) $ yang sama, kami memerlukan satu blok $ G $. Itu memiliki masukan $ R (s) $ dan keluarannya $ X (s) $. Diagram blok ini ditunjukkan pada gambar berikut.