Respon dari Sistem Orde Pertama
Dalam bab ini, mari kita bahas respon waktu dari sistem pesanan pertama. Perhatikan diagram blok berikut dari sistem kendali loop tertutup. Di sini, fungsi transfer loop terbuka, $ \ frac {1} {sT} $ dihubungkan dengan umpan balik negatif kesatuan.

Kita tahu bahwa fungsi transfer dari sistem kontrol loop tertutup memiliki umpan balik negatif kesatuan sebagai,
$$ \ frac {C (s)} {R (s)} = \ frac {G (s)} {1 + G (s)} $$
Gantikan, $ G (s) = \ frac {1} {sT} $ dalam persamaan di atas.
$$ \ frac {C (s)} {R (s)} = \ frac {\ frac {1} {sT}} {1+ \ frac {1} {sT}} = \ frac {1} {sT + 1} $$
Pangkat s adalah satu dalam suku penyebut. Oleh karena itu, fungsi transfer di atas adalah urutan pertama dan sistem disebut sebagaifirst order system.
Kita dapat menulis ulang persamaan di atas sebagai
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $$
Dimana,
C(s) adalah transformasi Laplace dari sinyal keluaran c (t),
R(s) adalah transformasi Laplace dari sinyal input r (t), dan
T adalah waktu yang konstan.
Ikuti langkah-langkah berikut untuk mendapatkan respon (keluaran) dari sistem urutan pertama dalam domain waktu.
Ambil transformasi Laplace dari sinyal input $ r (t) $.
Pertimbangkan persamaannya, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Gantikan nilai $ R (s) $ dalam persamaan di atas.
Lakukan pecahan parsial dari $ C (s) $ jika diperlukan.
Terapkan inverse Laplace transform ke $ C (s) $.
Pada bab sebelumnya, kita telah melihat sinyal uji standar seperti impuls, langkah, tanjakan, dan parabola. Sekarang mari kita cari tahu tanggapan dari sistem orde pertama untuk setiap masukan, satu per satu. Nama respons diberikan sesuai nama sinyal input. Misalnya, respons sistem untuk masukan impuls disebut sebagai respons impuls.
Respon Impuls Sistem Orde Pertama
Pertimbangkan unit impulse signal sebagai masukan untuk sistem orde pertama.
Jadi, $ r (t) = \ delta (t) $
Terapkan transformasi Laplace di kedua sisi.
$ R = 1 $
Pertimbangkan persamaannya, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Substitusi, $ R (s) = 1 $ dalam persamaan di atas.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) (1) = \ frac {1} {sT + 1} $$
Susun ulang persamaan di atas dalam salah satu bentuk standar transformasi Laplace.
$$ C (s) = \ frac {1} {T \ left (\ s + \ frac {1} {T} \ right)} \ Rightarrow C (s) = \ frac {1} {T} \ left (\ frac {1} {s + \ frac {1} {T}} \ kanan) $$
Menerapkan transformasi Laplace terbalik di kedua sisi.
$$ c (t) = \ frac {1} {T} e ^ \ kiri ({- \ frac {t} {T}} \ kanan) u (t) $$
Respon impuls unit ditunjukkan pada gambar berikut.
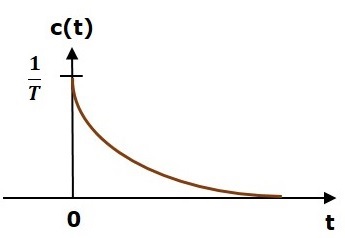
Itu unit impulse response, c (t) adalah sinyal peluruhan eksponensial untuk nilai positif 't' dan nol untuk nilai negatif 't'.
Langkah Respon Sistem First Order
Pertimbangkan unit step signal sebagai masukan untuk sistem pesanan pertama.
Jadi, $ r (t) = u (t) $
Terapkan transformasi Laplace di kedua sisi.
$$ R (s) = \ frac {1} {s} $$
Pertimbangkan persamaannya, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Gantikan, $ R (s) = \ frac {1} {s} $ dalam persamaan di atas.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s} \ right) = \ frac {1} {s \ left (sT + 1 \ kanan)} $$
Lakukan pecahan parsial dari C (s).
$$ C (s) = \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A} {s} + \ frac {B} {sT + 1} $$
$$ \ Rightarrow \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A \ left (sT + 1 \ right) + Bs} {s \ left (sT + 1 \ right)} $$
Di kedua sisi, suku penyebutnya sama. Jadi, mereka akan dibatalkan satu sama lain. Oleh karena itu, samakan suku pembilangnya.
$$ 1 = A \ kiri (sT + 1 \ kanan) + Bs $$
Dengan menyamakan konstanta di kedua sisi, Anda akan mendapatkan A = 1.
Gantikan, A = 1 dan samakan koefisien dari s istilah di kedua sisi.
$$ 0 = T + B \ Sisi Kanan B = -T $$
Gantikan, A = 1 dan B = −T dalam ekspansi pecahan parsial dari $ C (s) $.
$$ C (s) = \ frac {1} {s} - \ frac {T} {sT + 1} = \ frac {1} {s} - \ frac {T} {T \ left (s + \ frac { 1} {T} \ kanan)} $$
$$ \ Rightarrow C (s) = \ frac {1} {s} - \ frac {1} {s + \ frac {1} {T}} $$
Menerapkan transformasi Laplace terbalik di kedua sisi.
$$ c (t) = \ kiri (1-e ^ {- \ kiri (\ frac {t} {T} \ kanan)} \ kanan) u (t) $$
Itu unit step response, c (t) memiliki suku transien dan kondisi tunak.
Istilah sementara dalam respons langkah unit adalah -
$$ c_ {tr} (t) = - e ^ {- \ kiri (\ frac {t} {T} \ kanan)} u (t) $$
Istilah kondisi mapan dalam respons langkah satuan adalah -
$$ c_ {ss} (t) = u (t) $$
Gambar berikut menunjukkan respons langkah unit.

Nilai dari unit step response, c(t)adalah nol pada t = 0 dan untuk semua nilai negatif t. Secara bertahap meningkat dari nilai nol dan akhirnya mencapai satu dalam kondisi mapan. Jadi, nilai steady state bergantung pada besarnya input.
Respon Tanjakan Sistem Orde Pertama
Pertimbangkan unit ramp signal sebagai masukan untuk sistem orde pertama.
$ Jadi, r (t) = tu (t) $
Terapkan transformasi Laplace di kedua sisi.
$$ R (s) = \ frac {1} {s ^ 2} $$
Pertimbangkan persamaannya, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Gantikan, $ R (s) = \ frac {1} {s ^ 2} $ dalam persamaan di atas.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 2} \ right) = \ frac {1} {s ^ 2 ( sT + 1)} $$
Kerjakan pecahan parsial dari $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A} {s ^ 2} + \ frac {B} {s} + \ frac {C} {sT +1} $$
$$ \ Rightarrow \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A (sT + 1) + Bs (sT + 1) + Cs ^ 2} {s ^ 2 (sT + 1) } $$
Di kedua sisi, suku penyebutnya sama. Jadi, mereka akan dibatalkan satu sama lain. Oleh karena itu, samakan suku pembilangnya.
$$ 1 = A (sT + 1) + B (sT + 1) + Cs ^ 2 $$
Dengan menyamakan konstanta di kedua sisi, Anda akan mendapatkan A = 1.
Gantikan, A = 1 dan samakan koefisien dari suku-suku s di kedua sisi.
$$ 0 = T + B \ Sisi Kanan B = -T $$
Demikian pula, gantikan B = −T dan samakan koefisien dari $ s ^ 2 $ suku di kedua sisi. Anda akan mendapatkan $ C = T ^ 2 $.
Gantikan A = 1, B = −T dan $ C = T ^ 2 $ dalam ekspansi pecahan parsial $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T ^ 2} {sT + 1} = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T ^ 2} {T \ left (s + \ frac {1} {T} \ right)} $$
$$ \ Rightarrow C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T} {s + \ frac {1} {T}} $$
Menerapkan transformasi Laplace terbalik di kedua sisi.
$$ c (t) = \ kiri (t-T + Te ^ {- \ kiri (\ frac {t} {T} \ kanan)} \ kanan) u (t) $$
Itu unit ramp response, c (t) memiliki suku transien dan kondisi tunak.
Istilah transien dalam respons ramp unit adalah -
$$ c_ {tr} (t) = Te ^ {- \ kiri (\ frac {t} {T} \ kanan)} u (t) $$
Istilah kondisi tunak dalam respons ramp unit adalah -
$$ c_ {ss} (t) = (tT) u (t) $$
Gambar berikut menunjukkan respon ramp unit.

Itu unit ramp response, c (t) mengikuti sinyal input ramp unit untuk semua nilai positif t. Namun, ada penyimpangan satuan T dari sinyal masukan.
Respon Parabolik Sistem Orde Pertama
Pertimbangkan unit parabolic signal sebagai masukan untuk sistem orde pertama.
Jadi, $ r (t) = \ frac {t ^ 2} {2} u (t) $
Terapkan transformasi Laplace di kedua sisi.
$$ R (s) = \ frac {1} {s ^ 3} $$
Pertimbangkan persamaannya, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
Gantikan $ R (s) = \ frac {1} {s ^ 3} $ dalam persamaan di atas.
$$ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 3} \ right) = \ frac {1} {s ^ 3 ( sT + 1)} $$
Kerjakan pecahan parsial dari $ C (s) $.
$$ C (s) = \ frac {1} {s ^ 3 (sT + 1)} = \ frac {A} {s ^ 3} + \ frac {B} {s ^ 2} + \ frac {C} {s} + \ frac {D} {sT + 1} $$
Setelah menyederhanakan, Anda akan mendapatkan nilai A, B, C dan D sebagai 1, $ -T, \: T ^ 2 \: dan \: −T ^ 3 $. Gantikan nilai-nilai ini dalam ekspansi pecahan parsial C (s) di atas.
$ C = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 3} {sT + 1 } \: \ Rightarrow C (s) = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 2} {s + \ frac {1} {T}} $
Menerapkan transformasi Laplace terbalik di kedua sisi.
$$ c (t) = \ kiri (\ frac {t ^ 2} {2} -Tt + T ^ 2-T ^ 2e ^ {- \ left (\ frac {t} {T} \ kanan)} \ kanan ) u (t) $$
Itu unit parabolic response, c (t) memiliki suku transien dan kondisi tunak.
Istilah sementara dalam respons parabola unit adalah
$$ C_ {tr} (t) = - T ^ 2e ^ {- \ kiri (\ frac {t} {T} \ kanan)} u (t) $$
Istilah kondisi mapan dalam respons parabola unit adalah
$$ C_ {ss} (t) = \ kiri (\ frac {t ^ 2} {2} -Tt + T ^ 2 \ kanan) u (t) $$
Dari tanggapan ini, kita dapat menyimpulkan bahwa sistem kontrol urutan pertama tidak stabil dengan masukan ramp dan parabola karena tanggapan ini terus meningkat bahkan pada waktu yang tidak terbatas. Sistem kontrol orde pertama stabil dengan input impuls dan langkah karena respons ini memiliki output yang terbatas. Namun, impulse response tidak memiliki istilah steady state. Jadi, sinyal langkah banyak digunakan dalam domain waktu untuk menganalisis sistem kontrol dari tanggapannya.