Sistem Kontrol - Plot Pertanda
Bode plot atau Bode diagram terdiri dari dua plot -
- Plot besarnya
- Plot fase
Di kedua plot, sumbu x mewakili frekuensi sudut (skala logaritmik). Sedangkan yaxis merepresentasikan besaran (skala linier) fungsi transfer loop terbuka pada plot magnitudo dan sudut fasa (skala linier) dari fungsi transfer loop terbuka pada plot fase.
Itu magnitude dari fungsi transfer loop terbuka dalam dB adalah -
$$M=20\: \log|G(j\omega)H(j\omega)|$$
Itu phase angle dari fungsi transfer loop terbuka dalam derajat adalah -
$$\phi=\angle G(j\omega)H(j\omega)$$
Note - Basis logaritma adalah 10.
Dasar dari Bode Plots
Tabel berikut menunjukkan kemiringan, besaran dan nilai sudut fase dari istilah-istilah yang ada dalam fungsi transfer loop terbuka. Data ini berguna saat menggambar plot Bode.
| Jenis istilah | G (jω) H (jω) | Kemiringan (dB / des) | Besaran (dB) | Sudut fase (derajat) |
|---|---|---|---|---|
Konstan |
$K$ |
$0$ |
$20 \log K$ |
$0$ |
Nol di asalnya |
$j\omega$ |
$20$ |
$20 \log \omega$ |
$90$ |
'n' nol di asalnya |
$(j\omega)^n$ |
$20\: n$ |
$20\: n \log \omega$ |
$90\: n$ |
Kutub di asal |
$\frac{1}{j\omega}$ |
$-20$ |
$-20 \log \omega$ |
$-90 \: or \: 270$ |
kutub 'n' di asalnya |
$\frac{1}{(j\omega)^n}$ |
$-20\: n$ |
$-20 \: n \log \omega$ |
$-90 \: n \: or \: 270 \: n$ |
Nol sederhana |
$1+j\omega r$ |
$20$ |
$0\: for\: \omega < \frac{1}{r}$ $20\: \log \omega r\: for \: \omega > \frac{1}{r}$ |
$0 \: for \: \omega < \frac{1}{r}$ $90 \: for \: \omega > \frac{1}{r}$ |
Tiang sederhana |
$\frac{1}{1+j\omega r}$ |
$-20$ |
$0\: for\: \omega < \frac{1}{r}$ $-20\: \log \omega r\: for\: \omega > \frac{1}{r}$ |
$0 \: for \: \omega < \frac{1}{r}$ $-90\: or \: 270 \: for\: \omega > \frac{1}{r}$ |
Istilah turunan orde kedua |
$\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )$ |
$40$ |
$40\: \log\: \omega_n\: for \: \omega < \omega_n$ $20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $40 \: \log \: \omega\:for \:\omega > \omega_n$ |
$0 \: for \: \omega < \omega_n$ $90 \: for \: \omega = \omega_n$ $180 \: for \: \omega > \omega_n$ |
Suku integral orde dua |
$\frac{1}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$ |
$-40$ |
$-40\: \log\: \omega_n\: for \: \omega < \omega_n$ $-20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $-40 \: \log \: \omega\:for \:\omega > \omega_n$ |
$-0 \: for \: \omega < \omega_n$ $-90 \: for \: \omega = \omega_n$ $-180 \: for \: \omega > \omega_n$ |
Pertimbangkan fungsi transfer loop terbuka $G(s)H(s) = K$.
Besarnya $M = 20\: \log K$ dB
Sudut fase $\phi = 0$ derajat
Jika $K = 1$, maka besarnya 0 dB.
Jika $K > 1$, maka besarnya akan positif.
Jika $K < 1$, maka besarnya akan menjadi negatif.
Gambar berikut menunjukkan plot Bode yang sesuai.


Plot magnitudo adalah garis horizontal, yang tidak bergantung pada frekuensi. Garis 0 dB itu sendiri merupakan plot magnitudo jika nilai K adalah satu. Untuk nilai K positif, garis horizontal akan bergeser$20 \:\log K$dB di atas garis 0 dB. Untuk nilai negatif K, garis horizontal akan bergeser$20\: \log K$dB di bawah garis 0 dB. Garis derajat nol itu sendiri adalah plot fase untuk semua nilai positif K.
Pertimbangkan fungsi transfer loop terbuka $G(s)H(s) = s$.
Besarnya $M = 20 \log \omega$ dB
Sudut fase $\phi = 90^0$
Di $\omega = 0.1$ rad / detik, besarnya -20 dB.
Di $\omega = 1$ rad / detik, besarnya 0 dB.
Di $\omega = 10$ rad / detik, besarnya 20 dB.
Gambar berikut menunjukkan plot Bode yang sesuai.


Plot magnitudo adalah sebuah garis yang memiliki kemiringan 20 dB / des. Baris ini dimulai pada$\omega = 0.1$rad / detik memiliki besaran -20 dB dan berlanjut pada kemiringan yang sama. Ini menyentuh garis 0 dB pada$\omega = 1$rad / dtk. Dalam hal ini, plot fase adalah 90 0 garis.
Pertimbangkan fungsi transfer loop terbuka $G(s)H(s) = 1 + s\tau$.
Besarnya $M = 20\: log \sqrt{1 + \omega^2\tau^2}$ dB
Sudut fase $\phi = \tan^{-1}\omega\tau$ derajat
Untuk $ω < \frac{1}{\tau}$ , besarnya 0 dB dan sudut fasa 0 derajat.
Untuk $\omega > \frac{1}{\tau}$ , besarnya $20\: \log \omega\tau$dB dan sudut fasa adalah 90 0 .
Gambar berikut menunjukkan plot Bode yang sesuai.

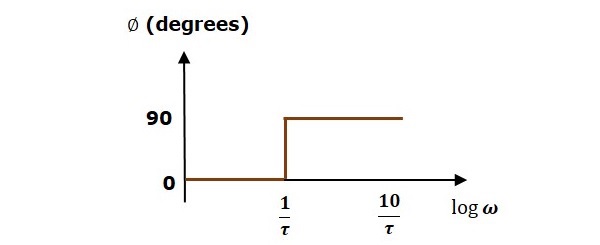
Plot magnitudo memiliki magnitudo 0 dB upto $\omega=\frac{1}{\tau}$rad / dtk. Dari$\omega = \frac{1}{\tau}$rad / detik, ini memiliki kemiringan 20 dB / des. Dalam hal ini, plot fase memiliki sudut fase 0 derajat ke atas$\omega = \frac{1}{\tau}$rad / detik dan dari sini, sudut fasa adalah 90 0 . Plot Bode ini disebutasymptotic Bode plot.
Karena plot magnitudo dan fase direpresentasikan dengan garis lurus, maka plot Exact Bode menyerupai plot Bode asimtotik. Satu-satunya perbedaan adalah bahwa plot Exact Bode akan memiliki kurva sederhana, bukan garis lurus.
Demikian pula, Anda dapat menggambar plot Bode untuk istilah lain dari fungsi transfer loop terbuka yang diberikan dalam tabel.