ジオメトリ-解決された例
Q1-ラインには
A -1つのエンドポイント
B -2つのエンドポイント
C -3つのエンドポイント
D-エンドポイントなし
Answer - D
Explanation
A line has no points.Q2-線分には
A -1つのエンドポイント
B -2つのエンドポイント
C -3つのエンドポイント
D-エンドポイントなし
Answer - B
Explanation
A line segment has two end points.Q3-光線には
A -1つのエンドポイント
B -2つのエンドポイント
C -3つのエンドポイント
D-エンドポイントなし
Answer - A
Explanation
A ray has one end point.Q 4-180°より大きく360°未満の角度は、
A-鋭角
B-鈍角
C-ストレートアングル
D-反射角
Answer - B
Explanation
An angle which is greater than 180° but less than 360° is called a reflex angle.Q5-62 °の補数はです。
A -118°
B -28°
C -38°
D -48°
Answer - B
Explanation
Complement of 62°= (90° – 62°) = 28°.Q6-60 °の補足は
A -30°
B -40°
C -120°
D -300°
Answer - B
Explanation
Supplement of 60° = (180°-60°) =120°.Q7を- 72℃40'の補数は
A -107°20 '
B -27°20 '
C -17°20 '
D -12°40 '
Answer - C
Explanation
Complement of 72° 40' = (90°-72° 40') =17° 20'.Q8-角度はその補足の5分の1です。角度の測度は
A -15°
B -30°
C -75°
D -150°
Answer - B
Explanation
x = 1/5 (180 – x )⇒ 5x = 180 – x ⇒ 6x = 180 ⇒ x = 30°.Q 9-角度がそれ自体の相補的な角度である場合、その測度は
A -30°
B -45°
C -60°
D -90°
Answer - B
Explanation
x=(90-x) ⇒ 2x = 90 ⇒ x = 45° .Q 10-図に示す光線によっていくつの角度が作られますか?

A -5
B -6
C -8
D -10
Answer - D
Explanation
The angle are ∠AOB , ∠BOC,∠COD,∠DOE,∠AOC,∠AOD, ∠AOE,∠BOD,∠BOD,∠COE.
Thus , 10 angle are formed.Q11-角度はその補数より24°大きいです。角度の測定値は
A -57°
B -47°
C -53°
D -66°
Answer - A
Explanation
x – (90-x ) = 24 ⇒ 2x = 114 ⇒ x = 57
∴ Required angle is 57°.Q 12 -An角度は、そのサプリメントよりも32°以下です。角度の測度は
A -37°
B -74°
C -48°
D -66°
Answer - A
Explanation
(180 –X) – X = 32 ⇒ 2x = 180 – 32 = 148 ⇒ x = 74.
Required angle is 74°.Q 13-2つの補助角度の比率は3:2です。小さい角度の測定
A -108°
B -81°
C -72°
D -66°
Answer - C
Explanation
Let the measures of the angle be (3x)° and (2x)°. Then,
3x+2x=180 ⇒ 5x = 180 ⇒ x = 36.
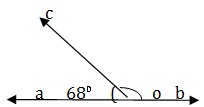
Smaller angle = (2x)° = (2*36)° = 72°.Q 14-与えられた図では、AOBは直線であり、∠AOC= 68°および∠BOC= x°です。xの値は
A -120°
B -22°
C -112°
D -132°
Answer - A
Explanation
Since ∠AOB is a straight angle , we have
X+ 68 = 180 ⇒ x= (180-68)° = 120°Q 15-与えられた図では、AOBは直線であり、∠AOC=(3x + 20)°および∠BOC=(4 x-36)°です。xの値は

A -32°
B -22°
C -26°
D -24°
Answer - B
Explanation
Since ∠AOB is a straight angle , we have
∠AOC + ∠ BOC =180°
⇒ 3x + 20 +4x – 36 = 180
⇒ 7x = 164 ⇒ x = 22.Q 16-与えられた図では、AOBは直線であり、∠AOC=(3x-8)°および∠COD= 50および∠BOD°=(x + 10)°です。xの値は

A -32°
B -42°
C -36°
D -52°
Answer - A
Explanation
Since ∠AOB is a straight angle , we have
∠AOC + ∠ COB + ∠ BOD = 180°
⇒ (3X – 8)° + 50° + (X+ 10)° = 180°
⇒ 4X = 128 ⇒ X = 32.