適性-ジオメトリ
ポイント
ポイントは正確な場所です
線分
2点AとBの間の直線経路は、線分ABと呼ばれます。線分には2つの端点があります。

レイ
線分ABを一方向に無期限に延長すると、光線ABが得られます。Ray ABには、1つのエンドポイント、つまりAがあります。

ライン
両方向に無期限に伸びる線分ABは線分ABと呼ばれます。

線には無限に多くの点が含まれます。
与えられた点を通して、無限に多くの線を引くことができます。
与えられた2つの点AとBを通過するために1本の線を引くことができます。
2本の線が一点で出会う。
2つの飛行機が一列に出会う。
共線
与えられた図では、点A、B、Cは同一線上にあります。

コンカレントライン
同じ点で交差する3つ以上の線は、同時線と呼ばれます。
角度
共通の端点Oを持つ2つの光線OAとOBは、角度AOBを形成し、∠AOBと記述されます。

角度の測定
OAからOBへの回転量は∠AOBの測度と呼ばれ、m(∠AOB)と表記されます。
360°の角度
元の位置OAから始まる光線OAが反時計回りにOを中心に回転し、完全に回転した後、元の位置に戻った場合、360°回転したと言います。この完全な回転は360°の等しい部分に分割されます。次に、各部分は1度と呼ばれ、1°と表記されます。
1°= 60分、60 'と表記
1分= 60秒、60 "と表記
角度の種類
Right angle -測定値が90°の角度は直角と呼ばれます。
Acute angle -測定値が90°未満の角度は鋭角と呼ばれます。
Obtuse angle -測定値が90°を超え180°未満の角度は、鈍角と呼ばれます。
Straight angle -測定値が180°の角度は、直線角度と呼ばれます。
Reflex angle -測定値が180°を超え360°未満の角度は、反射角と呼ばれます。
Complete angle -測定値が360°の角度は、完全な角度と呼ばれます。
Equal angle -2つの角度が同じメジャーである場合、それらは等しいと言われます。
Complementary angle測定値の合計が90の場合、2つの角度は相補的であると言われます。たとえば、65°と25°の角度は相補的な角度です。
Supplementary angle-それらの測定値の合計が180°の場合、2つの角度は補足的であると言われます。たとえば、70°と110°の角度は補足です。
Adjacent angle-2つの角度が同じ頂点と共通のアームを持ち、非共通のアームがコンマアームの両側にある場合、2つの角度は隣接角度と呼ばれます。与えられた図では、∠AOCと∠BOCは隣接する角度です。

重要な結果
光線が線上にある場合、そのように形成された2つの隣接する角度の合計は180°です。与えられた図では、光線CPは線AB上にあります。

∴ ∠ACD + ∠BCD = 180°.
線上の特定の点で線の同じ側に形成されるすべての角度の合計は180°です。与えられた図では、AOBの同じ側に4つの角度が形成されています。

∴ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180°.
点の周りのすべての角度の合計は360°です。与えられた図では、点Oの周りに5つの角度が形成されています。

∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°.
垂直方向に反対の角度
2本の線AバンドCDが点Oで交差する場合、AOC、BODおよびBOC、AODは、垂直方向に反対の角度の2つのペアです。垂直方向に反対の角度は常に等しくなります。
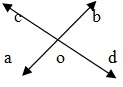
∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC
平行線
2つの線が同じ平面にあり、どちらかの側で生成されたときに交差しない場合、そのような線は平行であると言われ、L || mと記述します。
平行線を切断するトラバーサルライン

2本の平行線ABとCDを横断EFで切断します。次に
対応する角度は等しい
(∠1 = ∠5), (∠4= ∠8 ), (∠2 = ∠6) , (∠3 = ∠7)交互の内角は等しい。
(∠3 =∠5 ) and (∠4 =∠6 )内角は補足的です
∠4+∠5 = 180° and ∠3 +∠6 = 180°.三角形
3本の直線で囲まれた図形を三角形と呼びます。与えられた図では、ΔABCがあります。3つの頂点A、B、Cを持つ∆ABC。Inには、∠A、∠B、∠Cの3つの角度があります。AB、AC、BCの3つの側面があります。

三角形の種類
すべての辺が等しい三角形は、正三角形と呼ばれます。
2辺が等しい三角形は、二等辺三角形と呼ばれます。
すべての辺の長さが異なる三角形は、不等辺三角形と呼ばれます。
角度が90°の三角形は直角三角形と呼ばれます。
角度が90°から180°の三角形の1つは、鈍角三角形と呼ばれます。
それぞれの角度が鋭角である三角形は、鋭角三角形と呼ばれます。
三角形のすべての辺の合計は、三角形の周囲長と呼ばれます。
三角形の2つの辺の合計は、3番目の辺よりも大きくなります。
右側では∠B= 90°、我々はAC持っているABC角度を付ける2 = AB 2 + BC 2。これはピタゴラスの定理と呼ばれます。
四辺形
4本の直線で囲まれた図形を四辺形と呼びます。四辺形のすべての角度の合計は360°です。
Rectangle-四辺形は、その反対側が等しく、それぞれの角度が90°の場合、長方形と呼ばれます。与えられた図で。ABCDは長方形です。

Square-四辺形は、その辺がすべて等しく、各角度が90度の場合、正方形と呼ばれます。与えられた図で。ABCDは、AB = BC = CD = DAの正方形です。

Parallelogram-四辺形は、その反対側が平行である場合、平行四辺形と呼ばれます。与えられた図で。ABCDは、AB = DC&AD = BCの平行四辺形です。

Rhombus-すべての辺が等しい平行四辺形はひし形と呼ばれます。与えられた図で。ABCDは、AB = BC = CD = DA、AB ||であるひし形です。DCとAD || 紀元前。
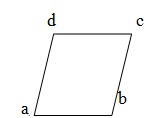
重要な事実
四辺形は、反対側が等しく、その対角線が等しい場合、長方形です。
すべての辺が等しく、対角線が等しい場合、四角形は正方形です。
反対側が等しい場合、四辺形は平行四辺形です。
四辺形は平行四辺形ですが、反対側が等しいが対角線が等しくない場合、長方形ではありません。
四辺形はひし形ですが、すべての辺が等しく、対角線が等しくない場合、正方形ではありません。
四辺形の結果
平行四辺形では、
反対側は等しい。
反対の角度は等しい。
各対角線は平行四辺形を二等分します。
平行四辺形の対角線は互いに二等分します。
長方形の対角線は同じです。
ひし形の対角線は互いに直角に二等分します。
サークルの結果

中心から弦への垂線は弦を二等分します。
3つの同一線上にない点を通過する円は1つだけです。
半円の角度は直角です。
外接四辺形の反対の角度は補足です。
円の同じセグメントの角度は同じです。
円の任意の点の接線は、接触点を通る半径に垂直です。
円の外側の点から円に接する2つの接線は等しい。
PTが円の接線で、PABが割線の場合、PA x PB = PT 2