볼록 최적화-최소 및 최대
로컬 최소화 또는 최소화
$ \ bar {x} \ in \ : S $는 $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ 인 경우 함수 $ f $의 로컬 최소값이라고합니다. forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ 여기서 $ N_ \ varepsilon \ left (\ bar {x} \ right) $는 $ \ bar {x} $의 이웃을 의미합니다. 즉, $ N_ \ varepsilon \ left (\ bar {x} \ right) $는 $ \ left \ | x- \ bar {x} \ 오른쪽 \ | <\ varepsilon $
로컬 Maxima 또는 Maximizer
$ \ bar {x} \ in \ : S $는 $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ 인 경우 $ f $ 함수의 극댓값이라고합니다. forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ 여기서 $ N_ \ varepsilon \ left (\ bar {x} \ right) $는 $ \ bar {x} $의 이웃을 의미합니다. 즉, $ N_ \ varepsilon \ left (\ bar {x} \ right) $는 $ \ left \ | x- \ bar {x} \ 오른쪽 \ | <\ varepsilon $
글로벌 최소값
$ \ bar {x} \ in \ : S $는 $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ 인 경우 $ f $ 함수의 전역 최소값이라고합니다. forall x \ in S $
글로벌 최대 값
$ \ bar {x} \ in \ : S $는 $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ 인 경우 $ f $ 함수의 전역 최대 값이라고합니다. forall x \ in S $
예
Step 1− $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ 오른쪽 | $
Solution −

위 함수의 그래프에서 로컬 최소값은 $ x = \ pm 2 $에서 발생하고 로컬 최대 값은 $ x = 0 $에서 발생 함이 분명합니다.
Step 2− 함수 $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ 오른쪽 | $
Solution −
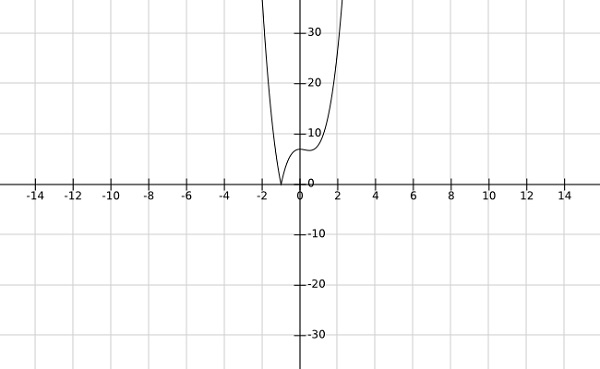
위 함수의 그래프에서 전역 최소값이 $ x = -1 $에서 발생하는 것이 분명합니다.