볼록 최적화-퀵 가이드
이 과정은 다양한 엔지니어링 및 과학 응용 프로그램에서 발생하는 비선형 최적화 문제를 해결하려는 학생들에게 유용합니다. 이 과정은 선형 계획법의 기본 이론으로 시작하여 볼록 세트 및 함수의 개념과 관련 용어를 소개하여 비선형 계획법 문제를 해결하는 데 필요한 다양한 정리를 설명합니다. 이 과정에서는 이러한 문제를 해결하는 데 사용되는 다양한 알고리즘을 소개합니다. 이러한 유형의 문제는 기계 학습, 전기 공학의 최적화 문제 등 다양한 응용 프로그램에서 발생합니다. 학생들은 고등학교 수학 개념과 미적분에 대한 사전 지식이 있어야합니다.
이 과정에서 학생들은 다음과 같은 최적화 문제를 해결하는 방법을 배웁니다. $min f\left ( x \right )$ 일부 제약이 있습니다.
이러한 문제는 다음과 같은 경우 쉽게 해결할 수 있습니다. $f\left ( x \right )$선형 함수이고 제약 조건이 선형 인 경우. 그런 다음 선형 계획법 문제 (LPP)라고합니다. 그러나 제약 조건이 비선형이면 위의 문제를 해결하기가 어렵습니다. 그래프에 함수를 그릴 수 없다면 최적화 분석을 시도하는 것은 한 가지 방법이 될 수 있지만 3 차원을 초과하는 경우 함수를 그릴 수 없습니다. 따라서 이러한 문제를 해결하기 위해 비선형 프로그래밍 또는 볼록 프로그래밍 기술이 제공됩니다. 이 튜토리얼에서는 이러한 기술을 배우는 데 중점을두고 결국에는 이러한 문제를 해결하기위한 몇 가지 알고리즘에 대해 알아 봅니다. 먼저 우리는 볼록 프로그래밍 문제의 기초가되는 볼록 집합의 개념을 가져올 것입니다. 그런 다음 볼록 함수를 도입하여 이러한 문제를 해결하기위한 몇 가지 중요한 정리와 이러한 정리를 기반으로하는 일부 알고리즘을 사용합니다.
용어
우주 $\mathbb{R}^n$ − 다음과 같이 정의 된 실수를 가진 n 차원 벡터입니다 − $\mathbb{R}^n=\left \{ \left ( x_1,x_2,...,x_n \right )^{\tau }:x_1,x_2,....,x_n \in \mathbb{R} \right \}$
우주 $\mathbb{R}^{mXn}$ − 모든 실수 값 행렬의 집합입니다. $mXn$.
방법론
선형 최적화라고도하는 선형 계획법은 관계가 본질적으로 선형 인 수학적 문제를 해결하는 데 사용되는 기술입니다. 선형 계획법의 기본 특성은objective function 일부에 따라 constraints. 목적 함수는 문제의 수학적 모델에서 얻은 선형 함수입니다. 제약 조건은 모델에 부과되는 조건이며 또한 선형입니다.
- 주어진 질문에서 목적 함수를 찾으십시오.
- 제약을 찾으십시오.
- 그래프에 제약 조건을 그립니다.
- 모든 제약의 교차로 형성되는 실행 가능 영역을 찾으십시오.
- 가능한 영역의 꼭지점을 찾으십시오.
- 이 꼭지점에서 목적 함수의 값을 찾으십시오.
- (질문에 따라) 목적 함수를 최대화하거나 최소화하는 정점이 정답입니다.
예
Step 1 − 최대화 $5x+3y$ 대상
$x+y\leq 2$,
$3x+y\leq 3$,
$x\geq 0 \:and \:y\geq 0$
Solution −
첫 번째 단계는 그래프에서 실행 가능한 영역을 찾는 것입니다.

그래프에서 분명히 알 수 있듯이 실행 가능 영역의 꼭지점은 다음과 같습니다.
$\left ( 0, 0 \right )\left ( 0, 2 \right )\left ( 1, 0 \right )\left ( \frac{1}{2}, \frac{3}{2} \right )$
허락하다 $f\left ( x, y \right )=5x+3y$
이 값을 목적 함수에 넣으면 다음과 같이됩니다.
$f\left ( 0, 0 \right )$= 0
$f\left ( 0, 2 \right )$= 6
$f\left ( 1, 0 \right )$= 5
$f\left ( \frac{1}{2}, \frac{3}{2} \right )$= 7
따라서 함수는 $\left ( \frac{1}{2}, \frac{3}{2} \right )$
Step 2− 한 시계 회사에서 디지털 및 기계식 시계를 생산합니다. 장기적인 예측은 매일 최소 100 개의 디지털 시계와 80 개의 기계식 시계에 대한 예상 수요를 나타냅니다. 생산 능력의 한계로 인해 매일 200 개 이상의 디지털 시계와 170 개의 기계식 시계를 만들 수 없습니다. 배송 계약을 충족하기 위해 매일 총 200 개 이상의 시계가 배송됩니다.
판매 된 각 디지털 시계가 $\$2$ loss, but each mechanical watch produces a $\$5$ 순이익을 극대화하려면 각 유형에서 매일 몇 개를 만들어야합니까?
Solution −
허락하다 $x$ 생산 된 디지털 시계의 수
$y$ 생산 된 기계식 시계의 수
질문에 따르면 매일 최소 100 개의 디지털 시계를 만들고 최대 200 개의 디지털 시계를 만들 수 있습니다.
$\Rightarrow 100 \leq \:x\leq 200$
마찬가지로 매일 최소 80 개의 기계식 시계가 만들어지고 최대 170 개의 기계식 시계가 만들어 질 수 있습니다.
$\Rightarrow 80 \leq \:y\leq 170$
매일 최소 200 개의 시계가 생산되기 때문입니다.
$\Rightarrow x +y\leq 200$
판매 된 각 디지털 시계는 $\$2$ loss, but each mechanical watch produces a $\$5$ 이익,
총 이익은 다음과 같이 계산할 수 있습니다.
$Profit =-2x + 5y$
그리고 우리는 이익을 극대화해야합니다. 따라서 질문은 다음과 같이 공식화 될 수 있습니다.
최대화 $-2x + 5y$ 대상
$100 \:\leq x\:\leq 200$
$80 \:\leq y\:\leq 170$
$x+y\:\leq 200$
위의 방정식을 그래프로 그리면,

실행 가능 영역의 정점은 다음과 같습니다.
$\left ( 100, 170\right )\left ( 200, 170\right )\left ( 200, 180\right )\left ( 120, 80\right ) and \left ( 100, 100\right )$
목적 함수의 최대 값은 $\left ( 100, 170\right )$ 따라서 순이익을 극대화하기 위해서는 디지털 시계 100 대와 기계식 시계 170 대를 생산해야한다.
노름은 벡터 또는 변수에 엄격하게 양의 값을 제공하는 함수입니다.
규범은 함수 다 $f:\mathbb{R}^n\rightarrow \mathbb{R}$
규범의 기본 특성은 다음과 같습니다.
허락하다 $X$ 다음과 같은 벡터 $X\in \mathbb{R}^n$
$\left \| x \right \|\geq 0$
$\left \| x \right \|= 0 \Leftrightarrow x= 0\forall x \in X$
$\left \|\alpha x \right \|=\left | \alpha \right |\left \| x \right \|\forall \:x \in X and \:\alpha \:is \:a \:scalar$
$\left \| x+y \right \|\leq \left \| x \right \|+\left \| y \right \| \forall x,y \in X$
$\left \| x-y \right \|\geq \left \| \left \| x \right \|-\left \| y \right \| \right \|$
정의에 따라 규범은 다음과 같이 계산됩니다.
$\left \| x \right \|_1=\displaystyle\sum\limits_{i=1}^n\left | x_i \right |$
$\left \| x \right \|_2=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^2 \right )^{\frac{1}{2}}$
$\left \| x \right \|_p=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^p \right )^{\frac{1}{p}},1 \leq p \leq \infty$
규범은 연속 함수입니다.
증명
정의에 따라 $x_n\rightarrow x$ 에 $X\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right ) $ 그때 $f\left ( x \right )$ 상수 함수입니다.
허락하다 $f\left ( x \right )=\left \| x \right \|$
따라서, $\left | f\left ( x_n \right )-f\left ( x \right ) \right |=\left | \left \| x_n \right \| -\left \| x \right \|\right |\leq \left | \left | x_n-x \right | \:\right |$
이후 $x_n \rightarrow x$ 그러므로, $\left \| x_n-x \right \|\rightarrow 0$
따라서 $\left | f\left ( x_n \right )-f\left ( x \right ) \right |\leq 0\Rightarrow \left | f\left ( x_n \right )-f\left ( x \right ) \right |=0\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right )$
따라서 규범은 연속 함수입니다.
내적은 벡터 쌍에 스칼라를 제공하는 함수입니다.
내부 제품 − $f:\mathbb{R}^n \times \mathbb{R}^n\rightarrow \kappa$ 어디 $\kappa$ 스칼라입니다.
내부 제품의 기본 특성은 다음과 같습니다.
허락하다 $X \in \mathbb{R}^n$
$\left \langle x,x \right \rangle\geq 0, \forall x \in X$
$\left \langle x,x \right \rangle=0\Leftrightarrow x=0, \forall x \in X$
$\left \langle \alpha x,y \right \rangle=\alpha \left \langle x,y \right \rangle,\forall \alpha \in \kappa \: and\: \forall x,y \in X$
$\left \langle x+y,z \right \rangle =\left \langle x,z \right \rangle +\left \langle y,z \right \rangle, \forall x,y,z \in X$
$\left \langle \overline{y,x} \right \rangle=\left ( x,y \right ), \forall x, y \in X$
Note −
규범과 내적 사이의 관계 : $\left \| x \right \|=\sqrt{\left ( x,x \right )}$
$\forall x,y \in \mathbb{R}^n,\left \langle x,y \right \rangle=x_1y_1+x_2y_2+...+x_ny_n$
예
1. 내적 찾기 $x=\left ( 1,2,1 \right )\: and \: y=\left ( 3,-1,3 \right )$
해결책
$\left \langle x,y \right \rangle =x_1y_1+x_2y_2+x_3y_3$
$\left \langle x,y \right \rangle=\left ( 1\times3 \right )+\left ( 2\times-1 \right )+\left ( 1\times3 \right )$
$\left \langle x,y \right \rangle=3+\left ( -2 \right )+3$
$\left \langle x,y \right \rangle=4$
2. 만약 $x=\left ( 4,9,1 \right ),y=\left ( -3,5,1 \right )$ 과 $z=\left ( 2,4,1 \right )$, 찾기 $\left ( x+y,z \right )$
해결책
아시다시피 $\left \langle x+y,z \right \rangle=\left \langle x,z \right \rangle+\left \langle y,z \right \rangle$
$\left \langle x+y,z \right \rangle=\left ( x_1z_1+x_2z_2+x_3z_3 \right )+\left ( y_1z_1+y_2z_2+y_3z_3 \right )$
$\left \langle x+y,z \right \rangle=\left \{ \left ( 4\times 2 \right )+\left ( 9\times 4 \right )+\left ( 1\times1 \right ) \right \}+$
$\left \{ \left ( -3\times2 \right )+\left ( 5\times4 \right )+\left ( 1\times 1\right ) \right \}$
$\left \langle x+y,z \right \rangle=\left ( 8+36+1 \right )+\left ( -6+20+1 \right )$
$\left \langle x+y,z \right \rangle=45+15$
$\left \langle x+y,z \right \rangle=60$
로컬 최소화 또는 최소화
$\bar{x}\in \:S$ 함수의 국소 최솟값이라고합니다. $f$ 만약 $f\left ( \bar{x} \right )\leq f\left ( x \right ),\forall x \in N_\varepsilon \left ( \bar{x} \right )$ 어디 $N_\varepsilon \left ( \bar{x} \right )$ 이웃을 의미 $\bar{x}$즉, $N_\varepsilon \left ( \bar{x} \right )$$ \ left \ | x- \ bar {x} \ 오른쪽 \ | <\ varepsilon $
로컬 Maxima 또는 Maximizer
$\bar{x}\in \:S$ 함수의 극댓값이라고합니다. $f$ 만약 $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in N_\varepsilon \left ( \bar{x} \right )$ 어디 $N_\varepsilon \left ( \bar{x} \right )$ 이웃을 의미 $\bar{x}$즉, $N_\varepsilon \left ( \bar{x} \right )$$ \ left \ | x- \ bar {x} \ 오른쪽 \ | <\ varepsilon $
글로벌 최소값
$\bar{x}\in \:S$ 함수의 글로벌 최소값이라고합니다. $f$ 만약 $f\left ( \bar{x} \right )\leq f\left ( x \right ), \forall x \in S$
글로벌 최대 값
$\bar{x}\in \:S$ 함수의 글로벌 최댓값이라고합니다. $f$ 만약 $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in S$
예
Step 1 − 로컬 최소값과 최대 값 찾기 $f\left ( \bar{x} \right )=\left | x^2-4 \right |$
Solution −

위 함수의 그래프에서 국소 최솟값이 $x= \pm 2$ 및 로컬 최대 값 $x = 0$
Step 2 − 함수에서 전역 최소값 찾기 $f\left (x \right )=\left | 4x^3-3x^2+7 \right |$
Solution −
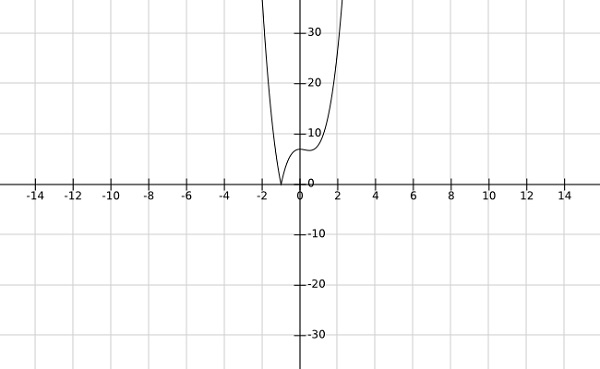
위 함수의 그래프에서 전역 최소값이 $x=-1$.
허락하다 $S\subseteq \mathbb{R}^n$ 세트 S의 두 점을 연결하는 선분이 S에도 속한다면 S 세트는 볼록하다고합니다. $x_1,x_2 \in S$, 다음 $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S$ 어디 $\lambda \in\left ( 0,1 \right )$.
Note −
- 두 볼록 세트의 결합은 볼록 일 수도 있고 아닐 수도 있습니다.
- 두 볼록 세트의 교차점은 항상 볼록합니다.
Proof
허락하다 $S_1$ 과 $S_2$ 두 개의 볼록한 세트입니다.
허락하다 $S_3=S_1 \cap S_2$
허락하다 $x_1,x_2 \in S_3$
이후 $S_3=S_1 \cap S_2$ 그러므로 $x_1,x_2 \in S_1$과 $x_1,x_2 \in S_2$
이후 $S_i$ 볼록 세트입니다. $\forall$ $i \in 1,2,$
그러므로 $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_i$ 어디 $\lambda \in \left ( 0,1 \right )$
그러므로 $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_1\cap S_2$
$\Rightarrow \lambda x_1+\left ( 1-\lambda \right )x_2 \in S_3$
그 후, $S_3$ 볼록 세트입니다.
양식의 가중 평균 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$,어디 $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$ 과 $\lambda_i\geq 0,\forall i \in \left [ 1,k \right ]$ 원추형 조합이라고합니다. $x_1,x_2,....x_k.$
양식의 가중 평균 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$, 어디 $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$ 아핀 조합이라고합니다. $x_1,x_2,....x_k.$
양식의 가중 평균 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ 선형 조합이라고합니다. $x_1,x_2,....x_k.$
예
Step 1 − 세트가 $S=\left \{ x \in \mathbb{R}^n:Cx\leq \alpha \right \}$ 볼록 세트입니다.
해결책
허락하다 $x_1$ 과 $x_2 \in S$
$\Rightarrow Cx_1\leq \alpha$ 과 $\:and \:Cx_2\leq \alpha$
표시하려면 :$\:\:y=\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\in S \:\forall \:\lambda \in\left ( 0,1 \right )$
$Cy=C\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=\lambda Cx_1+\left ( 1-\lambda \right )Cx_2$
$\Rightarrow Cy\leq \lambda \alpha+\left ( 1-\lambda \right )\alpha$
$\Rightarrow Cy\leq \alpha$
$\Rightarrow y\in S$
따라서, $S$ 볼록 세트입니다.
Step 2 − 세트가 $S=\left \{ \left ( x_1,x_2 \right )\in \mathbb{R}^2:x_{1}^{2}\leq 8x_2 \right \}$ 볼록 세트입니다.
해결책
허락하다 $x,y \in S$
허락하다 $x=\left ( x_1,x_2 \right )$ 과 $y=\left ( y_1,y_2 \right )$
$\Rightarrow x_{1}^{2}\leq 8x_2$ 과 $y_{1}^{2}\leq 8y_2$
보여주기 위해- $\lambda x+\left ( 1-\lambda \right )y\in S\Rightarrow \lambda \left ( x_1,x_2 \right )+\left (1-\lambda \right )\left ( y_1,y_2 \right ) \in S\Rightarrow \left [ \lambda x_1+\left ( 1- \lambda)y_2] \in S\right ) \right ]$
$Now, \left [\lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}=\lambda ^2x_{1}^{2}+\left ( 1-\lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1-\lambda \right )x_1y_1$
그러나 $2x_1y_1\leq x_{1}^{2}+y_{1}^{2}$
따라서,
$\left [ \lambda x_1 +\left ( 1-\lambda \right )y_1\right ]^{2}\leq \lambda ^2x_{1}^{2}+\left ( 1- \lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1- \lambda \right )\left ( x_{1}^{2}+y_{1}^{2} \right )$
$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq \lambda x_{1}^{2}+\left ( 1- \lambda \right )y_{1}^{2}$
$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\lambda x_2+8\left ( 1- \lambda \right )y_2$
$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\left [\lambda x_2+\left ( 1- \lambda \right )y_2 \right ]$
$\Rightarrow \lambda x+\left ( 1- \lambda \right )y \in S$
Step 3 − 세트 표시 $S \in \mathbb{R}^n$ 각 정수 k에 대해 볼록한 경우에만 k 점의 모든 볼록 조합 $S$ 에 $S$.
해결책
허락하다 $S$볼록한 집합이어야합니다. 그런 다음 보여주기 위해;
$c_1x_1+c_2x_2+.....+c_kx_k \in S, \displaystyle\sum\limits_{1}^k c_i=1,c_i\geq 0, \forall i \in 1,2,....,k$
귀납법에 의한 증명
에 대한 $k=1,x_1 \in S, c_1=1 \Rightarrow c_1x_1 \in S$
에 대한 $k=2,x_1,x_2 \in S, c_1+c_2=1$ S는 볼록 세트이므로
$\Rightarrow c_1x_1+c_2x_2 \in S.$
S의 m 점의 볼록한 조합이 S에 있다고합시다.
$c_1x_1+c_2x_2+...+c_mx_m \in S,\displaystyle\sum\limits_{1}^m c_i=1 ,c_i \geq 0, \forall i \in 1,2,...,m$
자,하자 $x_1,x_2....,x_m,x_{m+1} \in S$
허락하다 $x=\mu_1x_1+\mu_2x_2+...+\mu_mx_m+\mu_{m+1}x_{m+1}$
허락하다 $x=\left ( \mu_1+\mu_2+...+\mu_m \right )\frac{\mu_1x_1+\mu_2x_2+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}+\mu_{m+1}x_{m+1}$
허락하다 $y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}$
$\Rightarrow x=\left ( \mu_1+\mu_2+...+\mu_m \right )y+\mu_{m+1}x_{m+1}$
지금 $y \in S$ 계수의 합이 1이기 때문입니다.
$\Rightarrow x \in S$ S는 볼록 세트이고 $y,x_{m+1} \in S$
따라서 귀납법으로 증명되었습니다.
세트 $A$ 두 개의 다른 점에 대해이 점을 통과하는 선이 세트에있는 경우 아핀 세트라고합니다. $A$.
Note −
$S$ 포인트의 모든 아핀 조합을 포함하는 경우에만 아핀 집합입니다.
빈 세트와 싱글 톤 세트는 모두 아핀 및 볼록 세트입니다.
예를 들어 선형 방정식의 해는 아핀 집합입니다.
증명
S를 선형 방정식의해라 고합시다.
정의상 $S=\left \{ x \in \mathbb{R}^n:Ax=b \right \}$
허락하다 $x_1,x_2 \in S\Rightarrow Ax_1=b$ 과 $Ax_2=b$
를 입증하기 위해 : $A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=b, \forall \theta \in\left ( 0,1 \right )$
$A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=\theta Ax_1+\left ( 1-\theta \right )Ax_2=\theta b+\left ( 1-\theta \right )b=b$
따라서 S는 아핀 집합입니다.
정리
만약 $C$ 아핀 세트이고 $x_0 \in C$, 다음 세트 $V= C-x_0=\left \{ x-x_0:x \in C \right \}$ C의 부분 공간입니다.
증명
허락하다 $x_1,x_2 \in V$
표시하려면 : $\alpha x_1+\beta x_2 \in V$ 일부 $\alpha,\beta$
지금, $x_1+x_0 \in C$ 과 $x_2+x_0 \in C$ V의 정의
지금, $\alpha x_1+\beta x_2+x_0=\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0$
그러나 $\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0 \in C$ C는 아핀 집합이기 때문입니다.
따라서, $\alpha x_1+\beta x_2 \in V$
따라서 증명되었습니다.
S에있는 점 집합의 볼록 껍질은 내부 또는 경계에있는 S의 모든 점을 포함하는 가장 작은 볼록 영역의 경계입니다.
또는
허락하다 $S\subseteq \mathbb{R}^n$ 표시되는 S의 볼록 껍질 $Co\left ( S \right )$ by는 S의 모든 볼록한 조합의 모음입니다. $x \in Co\left ( S \right )$ 경우에만 $x \in \displaystyle\sum\limits_{i=1}^n \lambda_ix_i$, 어디 $\displaystyle\sum\limits_{1}^n \lambda_i=1$ 과 $\lambda_i \geq 0 \forall x_i \in S$
Remark − 평면에서 S 지점 집합의 Conves 헐은 볼록 다각형을 정의하고 다각형 경계에있는 S 지점은 다각형의 꼭지점을 정의합니다.
Theorem $Co\left ( S \right )= \left \{ x:x=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i,x_i \in S, \displaystyle\sum\limits_{i=1}^n \lambda_i=1,\lambda_i \geq 0 \right \}$ 볼록 껍질이 볼록 집합임을 보여줍니다.
증명
허락하다 $x_1,x_2 \in Co\left ( S \right )$, 다음 $x_1=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i$ 과 $x_2=\displaystyle\sum\limits_{i=1}^n \lambda_\gamma x_i$ 어디 $\displaystyle\sum\limits_{i=1}^n \lambda_i=1, \lambda_i\geq 0$ 과 $\displaystyle\sum\limits_{i=1}^n \gamma_i=1,\gamma_i\geq0$
에 대한 $\theta \in \left ( 0,1 \right ),\theta x_1+\left ( 1-\theta \right )x_2=\theta \displaystyle\sum\limits_{i=1}^n \lambda_ix_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n \gamma_ix_i$
$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n \lambda_i \theta x_i+\displaystyle\sum\limits_{i=1}^n \gamma_i\left ( 1-\theta \right )x_i$
$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]x_i$
계수를 고려하면,
$\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]=\theta \displaystyle\sum\limits_{i=1}^n \lambda_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n\gamma_i=\theta +\left ( 1-\theta \right )=1$
그 후, $\theta x_1+\left ( 1-\theta \right )x_2 \in Co\left ( S \right )$
따라서 볼록 껍질은 볼록 집합입니다.
S를 임의의 집합으로하자 $\mathbb{R}^n$.만약 $x \in Co\left ( S \right )$, 다음 $x \in Co\left ( x_1,x_2,....,x_n,x_{n+1} \right )$.
증명
이후 $x \in Co\left ( S\right )$, 다음 $x$ S에서 유한 한 수의 점의 볼록한 조합으로 표시됩니다. 즉,
$x=\displaystyle\sum\limits_{j=1}^k \lambda_jx_j,\displaystyle\sum\limits_{j=1}^k \lambda_j=1, \lambda_j \geq 0$ 과 $x_j \in S, \forall j \in \left ( 1,k \right )$
만약 $k \leq n+1$, 얻은 결과는 분명히 사실입니다.
만약 $k \geq n+1$, 다음 $\left ( x_2-x_1 \right )\left ( x_3-x_1 \right ),....., \left ( x_k-x_1 \right )$ 선형 의존적입니다.
$\Rightarrow \exists \mu _j \in \mathbb{R}, 2\leq j\leq k$ (모두 0이 아님) $\displaystyle\sum\limits_{j=2}^k \mu _j\left ( x_j-x_1 \right )=0$
밝히다 $\mu_1=-\displaystyle\sum\limits_{j=2}^k \mu _j$, 다음 $\displaystyle\sum\limits_{j=1}^k \mu_j x_j=0, \displaystyle\sum\limits_{j=1}^k \mu_j=0$
모두가 아닌 $\mu_j's$0과 같습니다. 이후$\displaystyle\sum\limits_{j=1}^k \mu_j=0$, 다음 중 하나 이상 $\mu_j > 0,1 \leq j \leq k$
그때, $x=\displaystyle\sum\limits_{1}^k \lambda_j x_j+0$
$x=\displaystyle\sum\limits_{1}^k \lambda_j x_j- \alpha \displaystyle\sum\limits_{1}^k \mu_j x_j$
$x=\displaystyle\sum\limits_{1}^k\left ( \lambda_j- \alpha\mu_j \right )x_j $
고르다 $\alpha$ 그런 $\alpha=min\left \{ \frac{\lambda_j}{\mu_j}, \mu_j\geq 0 \right \}=\frac{\lambda_j}{\mu _j},$ 일부 $i=1,2,...,k$
만약 $\mu_j\leq 0, \lambda_j-\alpha \mu_j\geq 0$
만약 $\mu_j> 0, then \:\frac{\lambda _j}{\mu_j}\geq \frac{\lambda_i}{\mu _i}=\alpha \Rightarrow \lambda_j-\alpha \mu_j\geq 0, j=1,2,...k$
특히, $\lambda_i-\alpha \mu_i=0$, 정의에 따라 $\alpha$
$x=\displaystyle\sum\limits_{j=1}^k \left ( \lambda_j- \alpha\mu_j\right )x_j$,어디
$\lambda_j- \alpha\mu_j\geq0$ 과 $\displaystyle\sum\limits_{j=1}^k\left ( \lambda_j- \alpha\mu_j\right )=1$ 과 $\lambda_i- \alpha\mu_i=0$
따라서 x는 최대 (k-1) 점의 볼록한 조합으로 나타낼 수 있습니다.
x가 (n + 1) 요소의 볼록한 조합으로 표시 될 때까지이 감소 과정을 반복 할 수 있습니다.
S를 비어 있지 않고 닫히고 경계가 지정된 집합 (간단한 집합이라고도 함)이라고합니다. $\mathbb{R}^n$ 그리고하자 $f:S\rightarrow \mathbb{R} $ S에 대한 연속 함수이면 문제 min $\left \{ f\left ( x \right ):x \in S \right \}$ 최소에 도달합니다.
증명
S는 비어 있지 않고 경계가 있으므로 하한이 있습니다.
$\alpha =Inf\left \{ f\left ( x \right ):x \in S \right \}$
이제 $S_j=\left \{ x \in S:\alpha \leq f\left ( x \right ) \leq \alpha +\delta ^j\right \} \forall j=1,2,...$ 과 $\delta \in \left ( 0,1 \right )$
infimium의 정의에 따르면 $S_j$ 비어 있지 않습니다. $j$.
일부 선택 $x_j \in S_j$ 시퀀스를 얻으려면 $\left \{ x_j \right \}$ ...에 대한 $j=1,2,...$
S가 경계이므로 시퀀스도 경계가 지정되고 수렴 하위 시퀀스가 있습니다. $\left \{ y_j \right \}$, 수렴 $\hat{x}$. 그 후$\hat{x}$ 한계점이고 S는 닫혀 있으므로 $\hat{x} \in S$. f는 연속적이므로$f\left ( y_i \right )\rightarrow f\left ( \hat{x} \right )$.
이후 $\alpha \leq f\left ( y_i \right )\leq \alpha+\delta^k, \alpha=\displaystyle\lim_{k\rightarrow \infty}f\left ( y_i \right )=f\left ( \hat{x} \right )$
그러므로, $\hat{x}$ 최소화 솔루션입니다.
비고
Weierstrass 정리에 필요한 두 가지 중요한 조건이 있습니다. 이들은 다음과 같습니다-
Step 1 − 집합 S는 경계 집합이어야합니다.
f \ left (x \ right) = x $ 함수를 고려하십시오.
무제한 세트이며 도메인의 어느 지점에서나 최소값이 있습니다.
따라서 최소값을 얻으려면 S를 제한해야합니다.
Step 2 − 세트 S를 닫아야합니다.
\ left (0,1 \ right) 도메인의 $ f \ left (x \ right) = \ frac {1} {x} $ 함수를 고려하십시오.
이 함수는 주어진 도메인에서 닫히지 않으며 최소값도 존재하지 않습니다.
따라서 최소값을 얻으려면 S를 닫아야합니다.
S를 $ \ mathbb {R} ^ n에있는 비어 있지 않은 닫힌 볼록 집합이라고합니다.$ and let $y \ notin S$, then $\ 존재$ a point $\ bar {x} \ in S$ with minimum distance from y, i.e.,$\ 왼쪽 \ | y- \ bar {x} \ 오른쪽 \ | \ leq \ 왼쪽 \ | yx \ 오른쪽 \ | \ forall x \ in S. $
또한 $ \ bar {x}$ is a minimizing point if and only if $\ 왼쪽 (y- \ 모자 {x} \ 오른쪽) ^ {T} \ 왼쪽 (x- \ 모자 {x} \ 오른쪽) \ leq 0$ or $\ left (y- \ hat {x}, x- \ hat {x} \ right) \ leq 0 $
증명
가장 가까운 지점의 존재
$ S \ ne \ phi, \ 존재 이후$ a point $\ hat {x} \ in S$ such that the minimum distance of S from y is less than or equal to $\ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ | $.
$ \ hat {S} = S \ cap \ left \ {x : \ left \ | 정의 yx \ 오른쪽 \ | \ leq \ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ | \ 오른쪽 \} $
$ \ hat {S} 이후$ is closed and bounded, and since norm is a continuous function, then by Weierstrass theorem, there exists a minimum point $\ hat {x} \ in S$ such that $\ 왼쪽 \ | y- \ hat {x} \ right \ | = Inf \ left \ {\ left \ | yx \ 오른쪽 \ |, x \ in S \ 오른쪽 \} $
고유성
$ \ bar {x} \ in S라고 가정합니다.$ such that $\ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ | = \ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ | = \ alpha $
S는 볼록하므로 $ \ frac {\ hat {x} + \ bar {x}} {2} \ in S $
하지만 $ \ left \ | y- \ frac {\ hat {x}-\ bar {x}} {2} \ right \ | \ leq \ frac {1} {2} \ left \ | y- \ hat {x} \ 오른쪽 \ | + \ frac {1} {2} \ 왼쪽 \ | y- \ bar {x} \ 오른쪽 \ | = \ alpha $
$ \ hat {x} $가 y에 가장 가깝기 때문에 완전 부등식 일 수 없습니다.
따라서 $ \ left \ | y- \ hat {x} \ 오른쪽 \ | = \ mu \ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ |$, for some $\ mu $
이제 $ \ left \ | \ mu \ 오른쪽 \ | = 1.$ If $\ mu = -1$, then $\ left (y- \ hat {x} \ right) =-\ left (y- \ hat {x} \ right) \ Rightarrow y = \ frac {\ hat {x} + \ bar {x}} {2} \ in S $
하지만 $ y \ in S$. Hence contradiction. Thus $\ mu = 1 \ Rightarrow \ hat {x} = \ bar {x} $
따라서 최소화 포인트는 고유합니다.
증명의 두 번째 부분에서 $ \ left (y- \ hat {x} \ right) ^ {\ tau} \ left (x- \ bar {x} \ right) \ leq 0$ for all $x \ in S $
지금,
$ \ 왼쪽 \ | yx \ 오른쪽 \ | ^ {2} = \ 왼쪽 \ | y- \ hat {x} + \ hat {x} -x \ 오른쪽 \ | ^ {2} = \ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ | ^ {2} + \ 왼쪽 \ | \ hat {x} -x \ 오른쪽 \ | ^ {2} +2 \ 왼쪽 (\ hat {x} -x \ right) ^ {\ tau} \ left (y- \ hat {x} \ right) $
$ \ Rightarrow \ 왼쪽 \ | yx \ 오른쪽 \ | ^ {2} \ geq \ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ | ^ {2}$ because $\ 왼쪽 \ | \ hat {x} -x \ right \ | ^ {2} \ geq 0$ and $\ left (\ hat {x}-x \ right) ^ {T} \ left (y- \ hat {x} \ right) \ geq 0 $
따라서 $ \ hat {x} $는 포인트를 최소화합니다.
반대로 $ \ hat {x} $가 minimizimg 포인트라고 가정합니다.
$ \ Rightarrow \ 왼쪽 \ | yx \ 오른쪽 \ | ^ {2} \ geq \ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ | ^ 2 \ forall x \ in S $
S는 볼록 세트이기 때문에.
$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) \ hat {x} = \ hat {x} + \ lambda \ left (x- \ hat {x} \ right) \ in S$ for $x \ in S$ and $\ lambda \ in \ left (0,1 \ right) $
이제 $ \ left \ | y- \ hat {x}-\ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ 오른쪽 \ | ^ 2 $
과
$ \ 왼쪽 \ | y- \ hat {x}-\ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ 오른쪽 \ | ^ {2} + \ lambda ^ 2 \ 왼쪽 \ | x- \ hat {x} \ 오른쪽 \ | ^ {2} -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) $
$ \ Rightarrow \ 왼쪽 \ | y- \ hat {x} \ 오른쪽 \ | ^ {2} + \ lambda ^ {2} \ 왼쪽 \ | x- \ hat {x} \ 오른쪽 \ | -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ geq \ left \ | y- \ hat {x} \ 오른쪽 \ | ^ {2} $
$ \ Rightarrow 2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq \ lambda ^ 2 \ left \ | x- \ hat {x} \ 오른쪽 \ | ^ 2 $
$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0 $
따라서 입증되었습니다.
S를 $ \ mathbb {R} ^ n에 설정된 비어 있지 않은 닫힌 볼록이라고합시다.$ and $y \ notin S$. Then, there exists a non zero vector $피$ and scalar $\베타$ such that $p ^ T y> \ beta$ and $p ^ T x <\ beta$ for each $x \ in S $
증명
S는 비어 있지 않은 닫힌 볼록 세트이고 $ y \ notin S이기 때문에$ thus by closest point theorem, there exists a unique minimizing point $\ hat {x} \ in S $에서
$ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 \ forall x \ in S $
$ p = \ left (y- \ hat {x} \ right) \ neq 0$ and $\ beta = \ hat {x} ^ T \ left (y- \ hat {x} \ right) = p ^ T \ hat {x} $.
그런 다음 $ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 $
$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ T \ left (x- \ hat {x} \ right) \ leq 0 $
$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ Tx \ leq \ left (y- \ hat {x} \ right) ^ T \ hat {x} = \ hat {x} ^ T \ left (y- \ hat {x} \ 오른쪽)$ i,e., $p ^ Tx \ leq \ beta $
또한 $ p ^ Ty- \ beta = \ left (y- \ hat {x} \ right) ^ Ty- \ hat {x} ^ T \ left (y- \ hat {x} \ right) $
$ = \ left (y- \ hat {x} \ right) ^ T \ left (yx \ right) = \ left \ | y- \ hat {x} \ 오른쪽 \ | ^ {2}> 0 $
$ \ Rightarrow p ^ Ty> \ beta $
이 정리는 초평면을 분리합니다. 위의 정리에 기반한 초평면은 다음과 같이 정의 할 수 있습니다.
$ S_1하자$ and $S_2$ are be non-empty subsets of $\ mathbb {R}$ and $H = \ left \ {X : A ^ TX = b \ right \} $는 초평면입니다.
초평면 H는 $ S_1을 분리한다고합니다.$ and $S_2$ if $A ^ TX \ leq b \ forall X \ in S_1$ and $A_TX \ geq b \ forall X \ in S_2 $
초평면 H는 $ S_1을 엄격하게 분리한다고합니다.$ and $S_2$ if $A ^ TX <b \ forall X \ in S_1$ and $A_TX> b \ forall X \ in S_2 $
초평면 H는 $ S_1을 강력하게 분리한다고합니다.$ and $S_2$ if $A ^ TX \ leq b \ forall X \ in S_1$ and $A_TX \ geq b + \ varepsilon \ forall X \ in S_2$, where $\ varepsilon $은 양의 스칼라입니다.
$ \ mathbb {R} ^ n의 비어 있지 않은 집합 C$ is said to be cone with vertex 0 if $x \ in C \ Rightarrow \ lambda x \ in C \ forall \ lambda \ geq 0 $.
세트 C는 원뿔과 마찬가지로 볼록한 경우 볼록 원뿔입니다.
예를 들어, $ y = \ left | x \ right | $는 볼록하지 않기 때문에 볼록한 원뿔이 아닙니다.
하지만 $ y \ geq \ left | x \ right | $는 볼록하고 원뿔이기 때문에 볼록 원뿔입니다.
Note − 원뿔 C는 $ x, y \ in C, x + y \ in C $ 인 경우에만 볼록합니다.
증명
C는 원뿔이므로 $ x, y \ in C \ Rightarrow \ lambda x \ in C$ and $\ mu y \ in C \ : \ forall \ : \ lambda, \ mu \ geq 0 $
$ \ lambda x + \ left (1- \ lambda \ right) y \ in C \ : \ forall \ : \ lambda \ in \ left (0, 1 \ right) $이면 C는 볼록입니다.
C는 원뿔이므로 $ \ lambda x \ in C$ and $\ left (1- \ lambda \ right) y \ in C \ Leftrightarrow x, y \ in C $
따라서 C는 $ x + y \ in C $이면 볼록합니다.
일반적으로 $ x_1, x_2 \ in C$, then, $\ lambda_1x_1 + \ lambda_2x_2 \ in C, \ forall \ lambda_1, \ lambda_2 \ geq 0 $
예
$ \ mathbb {R} ^ n $에있는 무한 벡터 집합의 원뿔 조합은 볼록 원뿔입니다.
빈 세트는 볼록 원뿔입니다.
모든 선형 함수는 볼록 원뿔입니다.
초평면은 선형이므로 볼록한 원뿔이기도합니다.
닫힌 절반 공간도 볼록한 원뿔입니다.
Note − 두 볼록 원뿔의 교차점은 볼록 원뿔이지만 그 결합은 볼록 원뿔 일 수도 있고 아닐 수도 있습니다.
$ \ mathbb {R} ^ n에서 S를 비어 있지 않은 집합으로 지정합니다.$ Then, the polar cone of S denoted by $S ^ *$ is given by $S ^ * = \ left \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \ : \ forall x \ in S \ right \} $.
말
S가 볼록하지 않더라도 폴라 콘은 항상 볼록합니다.
S가 빈 집합이면 $ S ^ * = \ mathbb {R} ^ n $.
극성은 직교성의 일반화로 볼 수 있습니다.
$ C \ subseteq \ mathbb {R} ^ n$ then the orthogonal space of C, denoted by $C ^ \ perp = \ left \ {y \ in \ mathbb {R} ^ n : \ left \ langle x, y \ right \ rangle = 0 \ forall x \ in C \ right \} $.
정리
$ S, S_1하자$ and $S_2$ be non empty sets in $\ mathbb {R} ^ n $ 다음 문장이 참입니다-
$ S ^ * $는 닫힌 볼록 원뿔입니다.
$ S \ subseteq S ^ {**}$ where $S ^ {**}$ is a polar cone of $S ^ * $.
$ S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*} $.
증명
Step 1 − $ S ^ * = \ left \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \ : \ forall \ : x \ in S \ right \} $
$ x_1, x_2 \ in S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0 $ and $x_ {2} ^ {T} x \ leq 0, \ forall x \ in S $
$ \ lambda \ in \ left (0, 1 \ right), \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] ^ Tx = \ left [\ left (\ lambda x_1 \ right ) ^ T + \ left \ {\ left (1- \ lambda \ right) x_ {2} \ right \} ^ {T} \ right] x, \ forall x \ in S $
$ = \ left [\ lambda x_ {1} ^ {T} + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ right] x = \ lambda x_ {1} ^ {T} x + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ leq 0 $
따라서 $ \ lambda x_1 + \ left (1- \ lambda \ right) x_ {2} \ in S ^ * $
따라서 $ S ^ * $는 볼록한 집합입니다.
$ \ lambda \ geq 0, p ^ {T} x \ leq 0, \ forall \ : x \ in S $
따라서 $ \ lambda p ^ T x \ leq 0, $
$ \ Rightarrow \ left (\ lambda p \ right) ^ T x \ leq 0 $
$ \ Rightarrow \ lambda p \ in S ^ * $
따라서 $ S ^ * $는 원뿔입니다.
$ S ^ * 표시$ is closed, i.e., to show if $p_n \ rightarrow p$ as $n \ rightarrow \ infty$, then $p \ in S ^ * $
$ \ forall x \ in S, p_ {n} ^ {T} xp ^ T x = \ left (p_n-p \ right) ^ T x $
$ p_n \ rightarrow p로$ as $n \ rightarrow \ infty \ Rightarrow \ left (p_n \ rightarrow p \ right) \ rightarrow 0 $
따라서 $ p_ {n} ^ {T} x \ rightarrow p ^ {T} x$. But $p_ {n} ^ {T} x \ leq 0, \ : \ forall x \ in S $
따라서 $ p ^ Tx \ leq 0, \ forall x \ in S $
$ \ Rightarrow p \ in S ^ * $
따라서 $ S ^ * $가 닫힙니다.
Step 2 − $ S ^ {**} = \ left \ {q \ in \ mathbb {R} ^ n : q ^ T p \ leq 0, \ forall p \ in S ^ * \ right \} $
$ x \ in S$, then $ \ forall p \ in S ^ *, p ^ T x \ leq 0 \ Rightarrow x ^ Tp \ leq 0 \ Rightarrow x \ in S ^ {**} $
따라서 $ S \ subseteq S ^ {**} $
Step 3 − $ S_2 ^ * = \ left \ {p \ in \ mathbb {R} ^ n : p ^ Tx \ leq 0, \ forall x \ in S_2 \ right \} $
$ S_1 \ subseteq S_2 \ Rightarrow \ forall x \ in S_2 \ Rightarrow \ forall x \ in S_1 $부터
따라서 $ \ hat {p} \ in S_2 ^ *, $then $\ hat {p} ^ Tx \ leq 0, \ forall x \ in S_2 $
$ \ Rightarrow \ hat {p} ^ Tx \ leq 0, \ forall x \ in S_1 $
$ \ Rightarrow \ hat {p} ^ T \ in S_1 ^ * $
$ \ Rightarrow S_2 ^ * \ subseteq S_1 ^ * $
정리
C를 비어 있지 않은 닫힌 볼록 원뿔로하고 $ C = C ^ ** $
증명
$ C = C ^ {**} $ by 이전 기본형.
증명하려면 : $ x \ in C ^ {**} \ subseteq C $
$ x \ in C ^ {**}$ and let $x \ notin C $
그런 다음 기본 분리 정리에 의해 벡터 $ p \ neq 0이 있습니다.$ and a scalar $\ alpha$ such that $p ^ Ty \ leq \ alpha, \ forall y \ in C $
따라서 $ p ^ Tx> \ alpha $
하지만 $ \ left (y = 0 \ right) \ in C$ and $p ^ Ty \ leq \ alpha, \ forall y \ in C \ Rightarrow \ alpha \ geq 0$ and $p ^ Tx> 0 $
$ p \ notin C ^ *$, then there exists some $\ bar {y} \ in C$ such that $p ^ T \ bar {y}> 0$ and $p ^ T \ left (\ lambda \ bar {y} \ right)$ can be made arbitrarily large by taking $\ lambda $ 충분히 큽니다.
이것은 $ p ^ Ty \ leq \ alpha, \ forall y \ in C $라는 사실과 모순됩니다.
따라서 $ p \ in C ^ * $
$ x \ in C ^ * = \ left \ {q : q ^ Tp \ leq 0, \ forall p \ in C ^ * \ right \} $ 이후
따라서 $ x ^ Tp \ leq 0 \ Rightarrow p ^ Tx \ leq 0 $
하지만 $ p ^ Tx> \ alpha $
따라서 모순입니다.
따라서 $ x \ in C $
따라서 $ C = C ^ {**} $.
$ \ alpha_1x_1 + \ alpha_2x_2 + .... + \ alpha_nx_n 형식의 포인트$ with $\ alpha_1, \ alpha_2, ..., \ alpha_n \ geq 0$ is called conic combination of $x_1, x_2, ..., x_n. $
$ x_i 인 경우$ are in convex cone C, then every conic combination of $x_i $도 C에 있습니다.
집합 C는 요소의 모든 원추 조합을 포함하는 경우 볼록 원뿔입니다.
원추형 선체
원추형 선체는 주어진 세트 S의 모든 원추형 조합의 세트로 정의되며 coni (S)로 표시됩니다.
따라서 $ coni \ left (S \ right) = \ left \ {\ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_ix_i : x_i \ in S, \ lambda_i \ in \ mathbb {R}, \ lambda_i \ geq 0, i = 1,2, ... \ 오른쪽 \} $
- 원추형 선체는 볼록한 집합입니다.
- 원점은 항상 원추형 선체에 속합니다.
$ \ mathbb {R} ^ n $에있는 집합은 제한된 수의 닫힌 반 공간의 교차점 인 경우 다면체라고합니다.
$ S = \ left \ {x \ in \ mathbb {R} ^ n : p_ {i} ^ {T} x \ leq \ alpha_i, i = 1,2, ...., n \ right \} $
예를 들면
$ \ 왼쪽 \ {x \ in \ mathbb {R} ^ n : AX = b \ 오른쪽 \} $
$ \ 왼쪽 \ {x \ in \ mathbb {R} ^ n : AX \ leq b \ 오른쪽 \} $
$ \ 왼쪽 \ {x \ in \ mathbb {R} ^ n : AX \ geq b \ 오른쪽 \} $
다면체 원뿔
$ \ mathbb {R} ^ n의 집합$ is said to be polyhedral cone if it is the intersection of a finite number of half spaces that contain the origin, i.e., $S = \ left \ {x \ in \ mathbb {R} ^ n : p_ {i} ^ {T} x \ leq 0, i = 1, 2, ... \ right \} $
폴리 토프
다면체는 경계가있는 다면체 집합입니다.
비고
- 폴리 토프는 유한 한 점 집합의 볼록 껍질입니다.
- 다면체 원뿔은 유한 벡터 집합에 의해 생성됩니다.
- 다면체 집합은 닫힌 집합입니다.
- 다면체 집합은 볼록 집합입니다.
S를 $ \ mathbb {R} ^ n에있는 볼록 집합이라고합시다.$. A vector $x \ in S$ is said to be a extreme point of S if $x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2$ with $x_1, x_2 \ in S$ and $\ lambda \ in \ left (0, 1 \ right) \ Rightarrow x = x_1 = x_2 $.
예
Step 1 − $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2 : x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 1 \ right \ } $
극단 점, $ E = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2 : x_ {1} ^ {2} + x_ {2} ^ {2} = 1 \ right \} $
Step 2 − $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2 : x_1 + x_2 <2, -x_1 + 2x_2 \ leq 2, x_1, x_2 \ geq 0 \ right \ } $
극단 점, $ E = \ left \ {\ left (0, 0 \ right), \ left (2, 0 \ right), \ left (0, 1 \ right), \ left (\ frac {2} {3 }, \ frac {4} {3} \ right) \ right \} $
Step 3 − S는 점 $ \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2, 4 \ 오른쪽), \ 왼쪽 (0,2 \ 오른쪽) \ 오른쪽 \} $
극단 점, $ E = \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2,4 \ right) \ 오른쪽 \} $
비고
볼록 세트 S의 모든 지점은 극단 지점의 볼록 조합으로 나타낼 수 있습니다.
$ \ mathbb {R} ^ n $의 폐쇄 및 경계 세트에만 해당됩니다.
무제한 세트의 경우에는 해당되지 않을 수 있습니다.
k 극점
볼록 집합의 한 점은 S 내에있는 k 차원 볼록 집합의 내부 점이고 S 내에있는 (k + 1) 차원 볼록 집합의 내부 점이 아닌 경우에만 k 극단이라고합니다. 기본적으로 볼록 세트 S의 경우 k 개의 극점은 k 차원의 열린면을 만듭니다.
S를 $ \ mathbb {R} ^ n에있는 닫힌 볼록 집합이라고합니다.$. A non zero vector $d \ in \ mathbb {R} ^ n$ is called a direction of S if for each $x \ in S, x + \ lambda d \ in S, \ forall \ lambda \ geq 0. $
양방향 $ d_1$ and $d_2$ of S are called distinct if $d \ neq \ alpha d_2$ for $ \ alpha> 0 $.
방향 $ d$ of $에스$ is said to be extreme direction if it cannot be written as a positive linear combination of two distinct directions, i.e., if $d = \ lambda _1d_1 + \ lambda _2d_2$ for $\ lambda _1, \ lambda _2> 0$, then $d_1 = \ alpha d_2$ for some $\ alpha $.
다른 방향은 극단 방향의 양의 조합으로 표현할 수 있습니다.
볼록 세트 $ S의 경우$, the direction d such that $x + \ lambda d \ in S$ for some $x \ in S$ and all $\ lambda \ geq0 $이 호출됩니다. recessive $ S $.
E를 특정 함수 $ f : S \ rightarrow$ over a non-empty convex set S in $\ mathbb {R} ^ n$ attains its maximum, then $이자형$ is called exposed face of $S $. 노출 된면의 방향을 노출 된 방향이라고합니다.
방향이 극단 인 광선을 극단 광선이라고합니다.
예
$ f \ left (x \ right) = y = \ left | x \ right |$, where $x \ in \ mathbb {R} ^ n$. Let d be unit vector in $\ mathbb {R} ^ n $
그러면 d는 모든 $ \ lambda \ geq 0, x + \ lambda d \ in f \ left (x \ right) $에 대해 함수 f의 방향입니다.
$ f : S \ rightarrow \ mathbb {R}$, where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ 왼쪽 (x \ 오른쪽)$ is said to be convex on S if $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ 오른쪽), \ forall \ lambda \ in \ left (0,1 \ right) $.
반면에 $ f : S \ rightarrow \ mathbb {R}$, where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ 왼쪽 (x \ 오른쪽)$ is said to be concave on S if $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ 오른쪽), \ forall \ lambda \ in \ left (0, 1 \ right) $.
$ f : S \ rightarrow \ mathbb {R}$ where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ 왼쪽 (x \ 오른쪽)$ is said to be strictly convex on S if $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <\ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right ), \ forall \ lambda \ in \ left (0, 1 \ right) $.
$ f : S \ rightarrow \ mathbb {R}$ where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ 왼쪽 (x \ 오른쪽)$ is said to be strictly concave on S if $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)> \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right ), \ forall \ lambda \ in \ left (0, 1 \ right) $.
예
선형 함수는 볼록하고 오목합니다.
$ f \ 왼쪽 (x \ 오른쪽) = \ 왼쪽 | x \ right | $는 볼록 함수입니다.
$ f \ left (x \ right) = \ frac {1} {x} $는 볼록 함수입니다.
정리
$ f_1, f_2, ..., f_k : \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ be convex functions. Consider the function $f \ left (x \ right) = \ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha_jf_j \ left (x \ right)$ where $\ alpha_j> 0, j = 1, 2, ... k,$ then $f \ left (x \ right) $는 볼록 함수입니다.
증명
$ f_1, f_2, ... f_k $는 볼록 함수이므로
따라서 $ f_i \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f_i \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_i \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right)$ and $i = 1, 2, ...., k $
$ f \ left (x \ right) $ 함수를 고려하십시오.
따라서,
$ f \ 왼쪽 (\ lambda x_1 + \ 왼쪽 (1- \ lambda \ 오른쪽) x_2 \ 오른쪽) $
$ = \ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha_jf_j \ left (\ lambda x_1 + 1- \ lambda \ right) x_2 \ leq \ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha_j \ 람다 f_j \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_j \ left (x_2 \ right) $
$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda \ left (\ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha _jf_j \ left ( x_1 \ right) \ right) + \ left (\ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha _jf_j \ left (x_2 \ right) \ right) $
$ \ 오른쪽 화살표 f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_2 \ right) \ leq \ left (1- \ lambda \ right) f \ 왼쪽 (x_2 \ 오른쪽) $
따라서 $ f \ left (x \ right) $는 볼록 함수입니다.
정리
$ f \ left (x \ right)하자$ be a convex function on a convex set $S \ subset \ mathbb {R} ^ n$ then a local minima of $S의 f \ left (x \ right) $는 전역 최소값입니다.
증명
$ \ hat {x}하자$ be a local minima for $f \ 왼쪽 (x \ 오른쪽)$ and $\ hat {x} $은 전역 최소값이 아닙니다.
따라서 $ \ exists \ hat {x} \ in S$ such that $f \ 왼쪽 (\ bar {x} \ 오른쪽) <f \ 왼쪽 (\ hat {x} \ 오른쪽) $
$ \ hat {x} 이후$ is a local minima, there exists neighbourhood $N_ \ varepsilon \ left (\ hat {x} \ right)$ such that $f \ left (\ hat {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $
But $f\left ( x \right )$ is a convex function on S, therefore for $\lambda \in \left ( 0, 1 \right )$
we have $\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}\leq \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left ( \bar{x} \right )$
$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left (\hat{x} \right )$
$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< f\left (\hat{x} \right ), \forall \lambda \in \left ( 0,1 \right )$
But for some $\lambda<1$ but close to 1, we have
$\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \in N_\varepsilon \left ( \hat{x} \right )\cap S$ and $f\left ( \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \right )< f\left ( \bar{x} \right )$
which is a contradiction.
Hence, $\bar{x}$ is a global minima.
Epigraph
let S be a non-empty subset in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$ then the epigraph of f denoted by epi(f) or $E_f$ is a subset of $\mathbb{R}^n+1$ defined by $E_f=\left \{ \left ( x,\alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\leq \alpha \right \}$
Hypograph
let S be a non-empty subset in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$, then the hypograph of f denoted by hyp(f) or $H_f=\left \{ \left ( x, \alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\geq \alpha \right \}$
Theorem
Let S be a non-empty convex set in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}^n$, then f is convex if and only if its epigraph $E_f$ is a convex set.
Proof
Let f is a convex function.
To show $E_f$ is a convex set.
Let $\left ( x_1, \alpha_1 \right ),\left ( x_2, \alpha_2 \right ) \in E_f,\lambda \in\left ( 0, 1 \right )$
To show $\lambda \left ( x_1,\alpha_1 \right )+\left ( 1-\lambda \right )\left ( x_2, \alpha_2 \right ) \in E_f$
$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2 \right ]\in E_f$
$f\left ( x_1 \right )\leq \alpha _1, f\left ( x_2\right )\leq \alpha _2$
Therefore, $f\left (\lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f \left ( x_2 \right )$
$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2$
Converse
Let $E_f$ is a convex set.
To show f is convex.
i.e., to show if $x_1, x_2 \in S,\lambda \left ( 0, 1\right )$
$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$
Let $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right ),f\left ( x_1 \right ), f\left ( x_2 \right ) \in \mathbb{R}$
Since $E_f$ is a convex set, $\left ( \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )\right )f\left ( x_2 \right )\in E_f$
Therefore, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$
Let S be a non-empty convex set in $\mathbb{R}^n$ and $f:S \rightarrow \mathbb{R}^n$. Then f is convex if and only if for each integer $k>0$
$x_1,x_2,...x_k \in S, \displaystyle\sum\limits_{i=1}^k \lambda_i=1, \lambda_i\geq 0, \forall i=1,2,s,k$, we have $f\left ( \displaystyle\sum\limits_{i=1}^k \lambda_ix_i \right )\leq \displaystyle\sum\limits_{i=1}^k \lambda _if\left ( x \right )$
Proof
By induction on k.
$k=1:x_1 \in S$ Therefore $f\left ( \lambda_1 x_1\right ) \leq \lambda_i f\left (x_1\right )$ because $\lambda_i=1$.
$k=2:\lambda_1+\lambda_2=1$ and $x_1, x_2 \in S$
Therefore, $\lambda_1x_1+\lambda_2x_2 \in S$
Hence by definition, $f\left ( \lambda_1 x_1 +\lambda_2 x_2 \right )\leq \lambda _1f\left ( x_1 \right )+\lambda _2f\left ( x_2 \right )$
Let the statement is true for $n < k$
Therefore,
$f\left ( \lambda_1 x_1+ \lambda_2 x_2+....+\lambda_k x_k\right )\leq \lambda_1 f\left (x_1 \right )+\lambda_2 f\left (x_2 \right )+...+\lambda_k f\left (x_k \right )$
$k=n+1:$ Let $x_1, x_2,....x_n,x_{n+1} \in S$ and $\displaystyle\sum\limits_{i=1}^{n+1}=1$
Therefore $\mu_1x_1+\mu_2x_2+.......+\mu_nx_n+\mu_{n+1} x_{n+1} \in S$
thus,$f\left (\mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1} x_{n+1} \right )$
$=f\left ( \left ( \mu_1+\mu_2+...+\mu_n \right)\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+\mu_3}+\mu_{n+1}x_{n+1} \right)$
$=f\left ( \mu_y+\mu_{n+1}x_{n+1} \right )$ where $\mu=\mu_1+\mu_2+...+\mu_n$ and
$y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n}$ and also $\mu_1+\mu_{n+1}=1,y \in S$
$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq \mu f\left ( y \right )+\mu_{n+1} f\left ( x_{n+1} \right )$
$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq$
$\left ( \mu_1+\mu_2+...+\mu_n \right )f\left ( \frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n} \right )+\mu_{n+1}f\left ( x_{n+1} \right )$
$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n +\mu_{n+1}x_{n+1}\right )\leq \left ( \mu_1+ \mu_2+ ...+\mu_n \right )$
$\left [ \frac{\mu_1}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_1 \right )+...+\frac{\mu_n}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_n \right ) \right ]+\mu_{n+1}f\left ( x_{n+1} \right )$
$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right )\leq \mu_1f\left ( x_1 \right )+\mu_2f\left ( x_2 \right )+....$
Hence Proved.
Let S be a non-empty open set in $\mathbb{R}^n$,then $f:S\rightarrow \mathbb{R}$ is said to be differentiable at $\hat{x} \in S$ if there exist a vector $\bigtriangledown f\left ( \hat{x} \right )$ called gradient vector and a function $\alpha :\mathbb{R}^n\rightarrow \mathbb{R}$ such that
$f\left ( x \right )=f\left ( \hat{x} \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x-\hat{x} \right )+\left \| x=\hat{x} \right \|\alpha \left ( \hat{x}, x-\hat{x} \right ), \forall x \in S$ where
$\alpha \left (\hat{x}, x-\hat{x} \right )\rightarrow 0 \bigtriangledown f\left ( \hat{x} \right )=\left [ \frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_2}...\frac{\partial f}{\partial x_n} \right ]_{x=\hat{x}}^{T}$
Theorem
let S be a non-empty, open convexset in $\mathbb{R}^n$ and let $f:S\rightarrow \mathbb{R}$ be differentiable on S. Then, f is convex if and only if for $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f\left ( x_2 \right )$
Proof
Let f be a convex function. i.e., for $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right )$
$f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$
$ \Rightarrow f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )+f\left ( x_2 \right )$
$ \Rightarrow\lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2+\lambda \left ( x_1-x_2 \right ) \right )-f\left ( x_2 \right )$
$\Rightarrow \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\lambda +$
$\left \| \lambda \left ( x_1-x_2 \right ) \right \|\alpha \left ( x_2,\lambda\left (x_1 - x_2 \right )-f\left ( x_2 \right ) \right )$
where $\alpha\left ( x_2, \lambda\left (x_1 - x_2 \right ) \right )\rightarrow 0$ as$\lambda \rightarrow 0$
Dividing by $\lambda$ on both sides, we get −
$f\left ( x_1 \right )-f\left ( x_2 \right ) \geq \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right )$
Converse
Let for $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f \left ( x_2 \right )$
To show that f is convex.
Since S is convex, $x_3=\lambda x_1+\left (1-\lambda \right )x_2 \in S, \lambda \in \left ( 0, 1 \right )$
Since $x_1, x_3 \in S$, therefore
$f\left ( x_1 \right )-f \left ( x_3 \right ) \geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 -x_3\right )$
$ \Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - \lambda x_1-\left (1-\lambda \right )x_2\right )$
$ \Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \left ( 1- \lambda\right )\bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - x_2\right )$
Since, $x_2, x_3 \in S$ therefore
$f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )$
$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-\lambda x_1-\left ( 1-\lambda \right )x_2 \right )$
$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \left ( -\lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )$
Thus, combining the above equations, we get −
$\lambda \left ( f\left ( x_1 \right )-f\left ( x_3 \right ) \right )+\left ( 1- \lambda \right )\left ( f\left ( x_2 \right )-f\left ( x_3 \right ) \right )\geq 0$
$\Rightarrow f\left ( x_3\right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$
Theorem
let S be a non-empty open convex set in $\mathbb{R}^n$ and let $f:S \rightarrow \mathbb{R}$ be differentiable on S, then f is convex on S if and only if for any $x_1,x_2 \in S,\left ( \bigtriangledown f \left ( x_2 \right )-\bigtriangledown f \left ( x_1 \right ) \right )^T \left ( x_2-x_1 \right ) \geq 0$
Proof
let f be a convex function, then using the previous theorem −
$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\leq f\left ( x_1 \right )-f\left ( x_2 \right )$ and
$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$
Adding the above two equations, we get −
$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq 0$
$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_1-x_2 \right )\leq 0$
$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_2-x_1 \right )\geq 0$
Converse
Let for any $x_1,x_2 \in S,\left (\bigtriangledown f \left ( x_2\right )- \bigtriangledown f \left ( x_1\right )\right )^T \left ( x_2-x_1\right )\geq 0$
To show that f is convex.
Let $x_1,x_2 \in S$, thus by mean value theorem, $\frac{f\left ( x_1\right )-f\left ( x_2\right )}{x_1-x_2}=\bigtriangledown f\left ( x\right ),x \in \left ( x_1-x_2\right ) \Rightarrow x= \lambda x_1+\left ( 1-\lambda\right )x_2$ because S is a convex set.
$\Rightarrow f\left ( x_1 \right )- f\left ( x_2 \right )=\left ( \bigtriangledown f\left ( x \right )^T \right )\left ( x_1-x_2 \right )$
for $x,x_1$, we know −
$\left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x-x_1 \right )\geq 0$
$\Rightarrow \left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( \lambda x_1+\left ( 1-\lambda \right )x_2-x_1 \right )\geq 0$
$\Rightarrow \left ( \bigtriangledown f\left ( x \right )- \bigtriangledown f\left ( x_1 \right )\right )^T\left ( 1- \lambda \right )\left ( x_2-x_1 \right )\geq 0$
$\Rightarrow \bigtriangledown f\left ( x \right )^T\left ( x_2-x_1 \right )\geq \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )$
Combining the above equations, we get −
$\Rightarrow \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$
Hence using the last theorem, f is a convex function.
Twice Differentiable function
Let S be a non-empty subset of $\mathbb{R}^n$ and let $f:S\rightarrow \mathbb{R}$ then f is said to be twice differentiable at $\bar{x} \in S$ if there exists a vector $\bigtriangledown f\left (\bar{x}\right ), a \:nXn$ matrix $H\left (x\right )$(called Hessian matrix) and a function $\alpha:\mathbb{R}^n \rightarrow \mathbb{R}$ such that $f\left ( x \right )=f\left ( \bar{x}+x-\bar{x} \right )=f\left ( \bar{x} \right )+\bigtriangledown f\left ( \bar{x} \right )^T\left ( x-\bar{x} \right )+\frac{1}{2}\left ( x-\bar{x} \right )H\left ( \bar{x} \right )\left ( x-\bar{x} \right )$
where $ \alpha \left ( \bar{x}, x-\bar{x} \right )\rightarrow Oasx\rightarrow \bar{x}$
Theorem
Let f be twice differentiable function. If $\bar{x}$ is a local minima, then $\bigtriangledown f\left ( \bar{x} \right )=0$ and the Hessian matrix $H\left ( \bar{x} \right )$ is a positive semidefinite.
Proof
Let $d \in \mathbb{R}^n$. Since f is twice differentiable at $\bar{x}$.
Therefore,
$f\left ( \bar{x} +\lambda d\right )=f\left ( \bar{x} \right )+\lambda \bigtriangledown f\left ( \bar{x} \right )^T d+\lambda^2d^TH\left ( \bar{x} \right )d+\lambda^2d^TH\left ( \bar{x} \right )d+$
$\lambda^2\left \| d \right \|^2\beta \left ( \bar{x}, \lambda d \right )$
But $\bigtriangledown f\left ( \bar{x} \right )=0$ and $\beta\left ( \bar{x}, \lambda d \right )\rightarrow 0$ as $\lambda \rightarrow 0$
$\Rightarrow f\left ( \bar{x} +\lambda d \right )-f\left ( \bar{x} \right )=\lambda ^2d^TH\left ( \bar{x} \right )d$
Since $\bar{x }$ is a local minima, there exists a $\delta > 0$ such that $f\left ( x \right )\leq f\left ( \bar{x}+\lambda d \right ), \forall \lambda \in \left ( 0,\delta \right )$
Theorem
Let $f:S \rightarrow \mathbb{R}^n$ where $S \subset \mathbb{R}^n$ be twice differentiable over S. If $\bigtriangledown f\left ( x\right )=0$ and $H\left ( \bar{x} \right )$ is positive semi-definite, for all $x \in S$, then $\bar{x}$ is a global optimal solution.
Proof
Since $H\left ( \bar{x} \right )$ is positive semi-definite, f is convex function over S. Since f is differentiable and convex at $\bar{x}$
$\bigtriangledown f\left ( \bar{x} \right )^T \left ( x-\bar{x} \right ) \leq f\left (x\right )-f\left (\bar{x}\right ),\forall x \in S$
Since $\bigtriangledown f\left ( \bar{x} \right )=0, f\left ( x \right )\geq f\left ( \bar{x} \right )$
Hence, $\bar{x}$ is a global optima.
Theorem
Suppose $\bar{x} \in S$ is a local optimal solution to the problem $f:S \rightarrow \mathbb{R}$ where S is a non-empty subset of $\mathbb{R}^n$ and S is convex. $min \:f\left ( x \right )$ where $x \in S$.
Then:
$\bar{x}$ is a global optimal solution.
If either $\bar{x}$ is strictly local minima or f is strictly convex function, then $\bar{x}$ is the unique global optimal solution and is also strong local minima.
Proof
Let $\bar{x}$ be another global optimal solution to the problem such that $x \neq \bar{x}$ and $f\left ( \bar{x} \right )=f\left ( \hat{x} \right )$
Since $\hat{x},\bar{x} \in S$ and S is convex, then $\frac{\hat{x}+\bar{x}}{2} \in S$ and f is strictly convex.
$\Rightarrow f\left ( \frac{\hat{x}+\bar{x}}{2} \right )< \frac{1}{2} f\left (\bar{x}\right )+\frac{1}{2} f\left (\hat{x}\right )=f\left (\hat{x}\right )$
This is contradiction.
Hence, $\hat{x}$ is a unique global optimal solution.
Corollary
Let $f:S \subset \mathbb{R}^n \rightarrow \mathbb{R}$ be a differentiable convex function where $\phi \neq S\subset \mathbb{R}^n$ is a convex set. Consider the problem $min f\left (x\right ),x \in S$,then $\bar{x}$ is an optimal solution if $\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right ) \geq 0,\forall x \in S.$
Proof
Let $\bar{x}$ is an optimal solution, i.e, $f\left (\bar{x}\right )\leq f\left (x\right ),\forall x \in S$
$\Rightarrow f\left (x\right )=f\left (\bar{x}\right )\geq 0$
$f\left (x\right )=f\left (\bar{x}\right )+\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )+\left \| x-\bar{x} \right \|\alpha \left ( \bar{x},x-\bar{x} \right )$
where $\alpha \left ( \bar{x},x-\bar{x} \right )\rightarrow 0$ as $x \rightarrow \bar{x}$
$\Rightarrow f\left (x\right )-f\left (\bar{x}\right )=\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )\geq 0$
Corollary
Let f be a differentiable convex function at $\bar{x}$,then $\bar{x}$ is global minimum iff $\bigtriangledown f\left (\bar{x}\right )=0$
Examples
$f\left (x\right )=\left (x^2-1\right )^{3}, x \in \mathbb{R}$.
$\bigtriangledown f\left (x\right )=0 \Rightarrow x= -1,0,1$.
$\bigtriangledown^2f\left (\pm 1 \right )=0, \bigtriangledown^2 f\left (0 \right )=6>0$.
$f\left (\pm 1 \right )=0,f\left (0 \right )=-1$
Hence, $f\left (x \right ) \geq -1=f\left (0 \right )\Rightarrow f\left (0 \right ) \leq f \left (x \right)\forall x \in \mathbb{R}$
$f\left (x \right )=x\log x$ defined on $S=\left \{ x \in \mathbb{R}, x> 0 \right \}$.
${f}'x=1+\log x$
${f}''x=\frac{1}{x}>0$
Thus, this function is strictly convex.
$f \left (x \right )=e^{x},x \in \mathbb{R}$ is strictly convex.
Let $f:S \rightarrow \mathbb{R}$ where $S \subset \mathbb{R}^n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1,x_2 \in S$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\lambda \in \left ( 0, 1 \right )$
For example, $f\left ( x \right )=x^{3}$
Let $f:S\rightarrow R $ where $S\subset \mathbb{R}^n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1, x_2 \in S$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\geq min\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}, \lambda \in \left ( 0, 1 \right )$
Remarks
- Every convex function is quasiconvex but the converse is not true.
- A function which is both quasiconvex and quasiconcave is called quasimonotone.
Theorem
Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasiconvex if and only if $S_{\alpha} =\left ( x \in S:f\left ( x \right )\leq \alpha \right \}$ is convex for each real number \alpha$
Proof
Let f is quasiconvex on S.
Let $x_1,x_2 \in S_{\alpha}$ therefore $x_1,x_2 \in S$ and $max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\leq \alpha$
Let $\lambda \in \left (0, 1 \right )$ and let $x=\lambda x_1+\left ( 1-\lambda \right )x_2\leq max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\Rightarrow x \in S$
Thus, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}\leq \alpha$
Therefore, $S_{\alpha}$ is convex.
Converse
Let $S_{\alpha}$ is convex for each $\alpha$
$x_1,x_2 \in S, \lambda \in \left ( 0,1\right )$
$x=\lambda x_1+\left ( 1-\lambda \right )x_2$
Let $x=\lambda x_1+\left ( 1-\lambda \right )x_2$
For $x_1, x_2 \in S_{\alpha}, \alpha= max \left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}$
$\Rightarrow \lambda x_1+\left (1-\lambda \right )x_2 \in S_{\alpha}$
$\Rightarrow f \left (\lambda x_1+\left (1-\lambda \right )x_2 \right )\leq \alpha$
Hence proved.
Theorem
Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasiconcave if and only if $S_{\alpha} =\left \{ x \in S:f\left ( x \right )\geq \alpha \right \}$ is convex for each real number $\alpha$.
Theorem
Let $f:S\rightarrow \mathbb{R}$ and S is a non empty convex set in $\mathbb{R}^n$. The function f is quasimonotone if and only if $S_{\alpha} =\left \{ x \in S:f\left ( x \right )= \alpha \right \}$ is convex for each real number $\alpha$.
Theorem
Let S be a non empty convex set in $\mathbb{R}^n$ and $f:S \rightarrow \mathbb{R}$ be differentiable on S, then f is quasiconvex if and only if for any $x_1,x_2 \in S$ and $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, we have $\bigtriangledown f\left ( x_2 \right )^T\left ( x_2-x_1 \right )\leq 0$
Proof
Let f be a quasiconvex function.
Let $x_1,x_2 \in S$ such that $f\left ( x_1 \right ) \leq f\left ( x_2 \right )$
By differentiability of f at $x_2, \lambda \in \left ( 0, 1 \right )$
$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=f\left ( x_2+\lambda \left (x_1-x_2 \right ) \right )=f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$
$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1-x_2 \right ) \right )$
$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )-f\left ( x_2 \right )-f\left ( x_2 \right )=\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$
$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x2, \lambda\left ( x_1-x_2 \right )\right )$
But since f is quasiconvex, $f \left ( \lambda x_1+ \left ( 1- \lambda \right )x_2 \right )\leq f \left (x_2 \right )$
$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right ) \right )\leq 0$
But $\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right )\right )\rightarrow 0$ as $\lambda \rightarrow 0$
Therefore, $\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right ) \leq 0$
Converse
let for $x_1,x_2 \in S$ and $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, $\bigtriangledown f\left ( x_2 \right )^T \left ( x_1,x_2 \right ) \leq 0$
To show that f is quasiconvex,ie, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq f\left ( x_2 \right )$
Proof by contradiction
Suppose there exists an $x_3= \lambda x_1+\left ( 1-\lambda \right )x_2$ such that $f\left ( x_2 \right )< f \left ( x_3 \right )$ for some $ \lambda \in \left ( 0, 1 \right )$
For $x_2$ and $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_2-x_3 \right ) \leq 0$
$\Rightarrow -\lambda \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )\leq 0$
$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\geq 0$
For $x_1$ and $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_3 \right ) \leq 0$
$\Rightarrow \left ( 1- \lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )\leq 0$
$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\leq 0$
thus, from the above equations, $\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )=0$
Define $U=\left \{ x:f\left ( x \right )\leq f\left ( x_2 \right ),x=\mu x_2+\left ( 1-\mu \right )x_3, \mu \in \left ( 0,1 \right ) \right \}$
Thus we can find $x_0 \in U$ such that $x_0 = \mu_0 x_2= \mu x_2+\left ( 1- \mu \right )x_3$ for some $\mu _0 \in \left ( 0,1 \right )$ which is nearest to $x_3$ and $\hat{x} \in \left ( x_0,x_1 \right )$ such that by mean value theorem,
$$\frac{f\left ( x_3\right )-f\left ( x_0\right )}{x_3-x_0}= \bigtriangledown f\left ( \hat{x}\right )$$
$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x_3-x_0 \right )$$
$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\mu_0 \lambda f\left ( \hat{x}\right )^T \left ( x_1-x_2 \right )$$
Since $x_0$ is a combination of $x_1$ and $x_2$ and $f\left (x_2 \right )< f\left ( \hat{x}\right )$
By repeating the starting procedure, $\bigtriangledown f \left ( \hat{x}\right )^T \left ( x_1-x_2\right )=0$
Thus, combining the above equations, we get:
$$f\left ( x_3\right )=f\left ( x_0 \right ) \leq f\left ( x_2\right )$$
$$\Rightarrow f\left ( x_3\right )\leq f\left ( x_2\right )$$
Hence, it is contradiction.
Examples
Step 1 − $f\left ( x\right )=X^3$
$Let f \left ( x_1\right )\leq f\left ( x_2\right )$
$\Rightarrow x_{1}^{3}\leq x_{2}^{3}\Rightarrow x_1\leq x_2$
$\bigtriangledown f\left ( x_2 \right )\left ( x_1-x_2 \right )=3x_{2}^{2}\left ( x_1-x_2 \right )\leq 0$
Thus, $f\left ( x\right )$ is quasiconvex.
Step 2 − $f\left ( x\right )=x_{1}^{3}+x_{2}^{3}$
Let $\hat{x_1}=\left ( 2, -2\right )$ and $\hat{x_2}=\left ( 1, 0\right )$
thus, $f\left ( \hat{x_1}\right )=0,f\left ( \hat{x_2}\right )=1 \Rightarrow f\left ( \hat{x_1}\right )\setminus < f \left ( \hat{x_2}\right )$
Thus, $\bigtriangledown f \left ( \hat{x_2}\right )^T \left ( \hat{x_1}- \hat{x_2}\right )= \left ( 3, 0\right )^T \left ( 1, -2\right )=3 >0$
Hence $f\left ( x\right )$ is not quasiconvex.
Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$ then f is said to be strictly quasicovex function if for each $x_1,x_2 \in S$ with $f\left ( x_1 \right ) \neq f\left ( x_2 \right )$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}$
Remarks
- Every strictly quasiconvex function is strictly convex.
- Strictly quasiconvex function does not imply quasiconvexity.
- Strictly quasiconvex function may not be strongly quasiconvex.
- Pseudoconvex function is a strictly quasiconvex function.
Theorem
Let $f:S\rightarrow \mathbb{R}^n$ be strictly quasiconvex function and S be a non-empty convex set in $\mathbb{R}^n$.Consider the problem: $min \:f\left ( x \right ), x \in S$. If $\hat{x}$ is local optimal solution, then $\bar{x}$ is global optimal solution.
Proof
Let there exists $ \bar{x} \in S$ such that $f\left ( \bar{x}\right )\leq f \left ( \hat{x}\right )$
Since $\bar{x},\hat{x} \in S$ and S is convex set, therefore,
$$\lambda \bar{x}+\left ( 1-\lambda \right )\hat{x}\in S, \forall \lambda \in \left ( 0,1 \right )$$
Since $\hat{x}$ is local minima, $f\left ( \hat{x} \right ) \leq f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right ), \forall \lambda \in \left ( 0,\delta \right )$
Since f is strictly quasiconvex.
$$f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right )< max \left \{ f\left ( \hat{x} \right ),f\left ( \bar{x} \right ) \right \}=f\left ( \hat{x} \right )$$
Hence, it is contradiction.
Strictly quasiconcave function
Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$, then f is saud to be strictly quasicovex function if for each $x_1,x_2 \in S$ with $f\left (x_1\right )\neq f\left (x_2\right )$, we have
$$f\left (\lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$$.
Examples
$f\left (x\right )=x^2-2$
It is a strictly quasiconvex function because if we take any two points $x_1,x_2$ in the domain that satisfy the constraints in the definition $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )< max \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$ As the function is decreasing in the negative x-axis and it is increasing in the positive x-axis (since it is a parabola).
$f\left (x\right )=-x^2$
It is not a strictly quasiconvex function because if we take take $x_1=1$ and $x_2=-1$ and $\lambda=0.5$, then $f\left (x_1\right )=-1=f\left (x_2\right )$ but $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )=0$ Therefore it does not satisfy the conditions stated in the definition. But it is a quasiconcave function because if we take any two points in the domain that satisfy the constraints in the definition $f\left ( \lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$. As the function is increasing in the negative x-axis and it is decreasing in the positive x-axis.
Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$ then f is strongly quasiconvex function if for any $x_1,x_2 \in S$ with $\left ( x_1 \right ) \neq \left ( x_2 \right )$, we have $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\forall \lambda \in \left ( 0,1\right )$
Theorem
A quasiconvex function $f:S\rightarrow \mathbb{R}^n$ on a non-empty convex set S in $\mathbb{R}^n$ is strongly quasiconvex function if it is not constant on a line segment joining any points of S.
Proof
Let f is quasiconvex function and it is not constant on a line segment joining any points of S.
Suppose f is not strongly quasiconvex function.
There exist $x_1,x_2 \in S$ with $x_1 \neq x_2$ such that
$$f\left ( z \right )\geq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}, \forall z= \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \in \left ( 0,1 \right )$$
$\Rightarrow f\left ( x_1 \right )\leq f\left ( z \right )$ and $f\left ( x_2 \right )\leq f\left ( z \right )$
Since f is not constant in $\left [ x_1,z \right ]$ and $\left [z,x_2 \right ] $
So there exists $u \in \left [ x_1,z \right ]$ and $v=\left [ z,x_2 \right ]$
$$\Rightarrow u= \mu_1x_1+\left ( 1-\mu_1\right )z,v=\mu_2z+\left ( 1- \mu_2\right )x_2$$
Since f is quasiconvex,
$$\Rightarrow f\left ( u \right )\leq max\left \{ f\left ( x_1 \right ),f \left ( z \right ) \right \}=f\left ( z \right )\:\: and \:\:f \left ( v \right ) \leq max \left \{ f\left ( z \right ),f\left ( x_2 \right ) \right \}$$
$$\Rightarrow f\left ( u \right )\leq f\left ( z \right ) \:\: and \:\: f\left ( v \right )\leq f\left ( z \right )$$
$$\Rightarrow max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$$
But z is any point between u and v, if any of them are equal, then f is constant.
Therefore, $max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$
which contradicts the quasiconvexity of f as $z \in \left [ u,v \right ]$.
Hence f is strongly quasiconvex function.
Theorem
Let $f:S\rightarrow \mathbb{R}^n$ and S be a non-empty convex set in $\mathbb{R}^n$. If $\hat{x}$ is local optimal solution, then $\hat{x}$ is unique global optimal solution.
Proof
Since a strong quasiconvex function is also strictly quasiconvex function, thus a local optimal solution is global optimal solution.
Uniqueness − Let f attains global optimal solution at two points $u,v \in S$
$$\Rightarrow f\left ( u \right ) \leq f\left ( x \right ).\forall x \in S\:\: and \:\:f\left ( v \right ) \leq f\left ( x \right ).\forall x \in S$$
If u is global optimal solution, $f\left ( u \right )\leq f\left ( v \right )$ and $f\left ( v \right )\leq f\left ( u\right )\Rightarrow f\left ( u \right )=f\left ( v\right )$
$$f\left ( \lambda u+\left ( 1-\lambda\right )v\right )< max \left \{f\left ( u \right ),f\left ( v \right ) \right \}=f\left ( u \right )$$
which is a contradiction.
Hence there exists only one global optimal solution.
Remarks
- A strongly quasiconvex function is also strictly quasiconvex fucntion.
- A strictly convex function may or may not be strongly quasiconvex.
- A differentiable strictly convex is strongly quasiconvex.
Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1,x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )\geq f\left ( x_1 \right )$, or equivalently if $f\left ( x_1 \right )>f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$
Pseudoconcave function
Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1, x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )\leq f\left ( x_1 \right )$, or equivalently if $f\left ( x_1 \right )>f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )>0$
Remarks
If a function is both pseudoconvex and pseudoconcave, then is is called pseudolinear.
A differentiable convex function is also pseudoconvex.
A pseudoconvex function may not be convex. For example,
$f\left ( x \right )=x+x^3$ is not convex. If $x_1 \leq x_2,x_{1}^{3} \leq x_{2}^{3}$
Thus,$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )=\left ( 1+3x_{1}^{2} \right )\left ( x_2-x_1 \right ) \geq 0$
And, $f\left ( x_2 \right )-f\left ( x_1 \right )=\left ( x_2-x_1 \right )+\left ( x_{2}^{3} -x_{1}^{3}\right )\geq 0$
$\Rightarrow f\left ( x_2 \right )\geq f\left ( x_1 \right )$
Thus, it is pseudoconvex.
A pseudoconvex function is strictly quasiconvex. Thus, every local minima of pseudoconvex is also global minima.
Strictly pseudoconvex function
Let $f:S\rightarrow \mathbb{R}$ be a differentiable function and S be a non-empty convex set in $\mathbb{R}^n$, then f is said to be pseudoconvex if for each $x_1,x_2 \in S$ with $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, we have $f\left ( x_2 \right )> f\left ( x_1 \right )$,or equivalently if $f\left ( x_1 \right )\geq f\left ( x_2 \right )$ then $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$
Theorem
Let f be a pseudoconvex function and suppose $\bigtriangledown f\left ( \hat{x}\right )=0$ for some $\hat{x} \in S$, then $\hat{x}$ is global optimal solution of f over S.
Proof
Let $\hat{x}$ be a critical point of f, ie, $\bigtriangledown f\left ( \hat{x}\right )=0$
Since f is pseudoconvex function, for $x \in S,$ we have
$$\bigtriangledown f\left ( \hat{x}\right )\left ( x-\hat{x}\right )=0 \Rightarrow f\left ( \hat{x}\right )\leq f\left ( x\right ), \forall x \in S$$
Hence, $\hat{x}$ is global optimal solution.
Remark
If f is strictly pseudoconvex function, $\hat{x}$ is unique global optimal solution.
Theorem
If f is differentiable pseudoconvex function over S, then f is both strictly quasiconvex as well as quasiconvex function.
Remarks
The sum of two pseudoconvex fucntions defined on an open set S of $\mathbb{R}^n$ may not be pseudoconvex.
Let $f:S\rightarrow \mathbb{R}$ be a quasiconvex function and S be a non-empty convex subset of $\mathbb{R}^n$ then f is pseudoconvex if and only if every critical point is a global minima of f over S.
Let S be a non-empty convex subset of $\mathbb{R}^n$ and $f:S\rightarrow \mathbb{R}$ be a function such that $\bigtriangledown f\left ( x\right )\neq 0$ for every $x \in S$ then f is pseudoconvex if and only if it is a quasiconvex function.
There are four types of convex programming problems −
Step 1 − $min \:f\left ( x \right )$, where $x \in S$ and S be a non-empty convex set in $\mathbb{R}^n$ and $f\left ( x \right )$ is convex function.
Step 2 − $min \: f\left ( x \right ), x \in \mathbb{R}^n$ subject to
$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ and $g_i\left ( x \right )$ is a convex function.
$g_i\left ( x \right ) \leq 0,m_1+1 \leq m_2$ and $g_i\left ( x \right )$ is a concave function.
$g_i\left ( x \right ) = 0, m_2+1 \leq m$ and $g_i\left ( x \right )$ is a linear function.
where $f\left ( x \right )$ is a convex fucntion.
Step 3 − $max \:f\left ( x \right )$ where $x \in S$ and S be a non-empty convex set in $\mathbb{R}^n$ and $f\left ( x \right )$ is concave function.
Step 4 − $min \:f\left ( x \right )$, where $x \in \mathbb{R}^n$ subject to
$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ and $g_i\left ( x \right )$ is a convex function.
$g_i\left ( x \right ) \leq 0, m_1+1 \leq m_2$ and $g_i\left ( x \right )$ is a concave function.
$g_i\left ( x \right ) = 0,m_2+1 \leq m$ and $g_i\left ( x \right )$ is a linear function.
where $f\left ( x \right )$ is a concave function.
Cone of feasible direction
Let S be a non-empty set in $\mathbb{R}^n$ and let $\hat{x} \in \:Closure\left ( S \right )$, then the cone of feasible direction of S at $\hat{x}$, denoted by D, is defined as $D=\left \{ d:d\neq 0,\hat{x}+\lambda d \in S, \lambda \in \left ( 0, \delta \right ), \delta > 0 \right \}$
Each non-zero vector $d \in D$ is called feasible direction.
For a given function $f:\mathbb{R}^n \Rightarrow \mathbb{R}$ the cone of improving direction at $\hat{x}$ is denoted by F and is given by
$$F=\left \{ d:f\left ( \hat{x}+\lambda d \right )\leq f\left ( \hat{x} \right ),\forall \lambda \in \left ( 0,\delta \right ), \delta >0 \right \}$$
Each direction $d \in F$ is called an improving direction or descent direction of f at $\hat{x}$
Theorem
Necessary Condition
Consider the problem $min f\left ( x \right )$ such that $x \in S$ where S be a non-empty set in $\mathbb{R}^n$. Suppose f is differentiable at a point $\hat{x} \in S$. If $\hat{x}$ is a local optimal solution, then $F_0 \cap D= \phi$ where $F_0=\left \{ d:\bigtriangledown f\left ( \hat{x} \right )^T d < 0 \right \}$ and D is a cone of feasible direction.
Sufficient Condition
If $F_0 \cap D= \phi$ f is a pseudoconvex function at $\hat{x}$ and there exists a neighbourhood of $\hat{x},N_\varepsilon \left ( \hat{x} \right ), \varepsilon > 0$ such that $d=x-\hat{x}\in D$ for any $x \in S \cap N_\varepsilon \left ( \hat{x} \right )$, then $\hat{x}$ is local optimal solution.
Proof
Necessary Condition
Let $F_0 \cap D\neq \phi$, ie, there exists a $d \in F_0 \cap D$ such that $d \in F_0$ and $d\in D$
Since $d \in D$, therefore there exists $\delta_1 >0$ such that $\hat{x}+\lambda d \in S, \lambda \in \left ( 0,\delta_1 \right ).$
Since $d \in F_0$, therefore $\bigtriangledown f \left ( \hat{x}\right )^T d <0$
Thus, there exists $\delta_2>0$ such that $f\left ( \hat{x}+\lambda d\right )< f\left ( \hat{x}\right ),\forall \lambda \in f \left ( 0,\delta_2 \right )$
Let $\delta=min \left \{\delta_1,\delta_2 \right \}$
Then $\hat{x}+\lambda d \in S, f\left (\hat{x}+\lambda d \right ) < f\left ( \hat{x} \right ),\forall \lambda \in f \left ( 0,\delta \right )$
But $\hat{x}$ is local optimal solution.
Hence it is contradiction.
Thus $F_0\cap D=\phi$
Sufficient Condition
Let $F_0 \cap D\neq \phi$ nd let f be a pseudoconvex function.
Let there exists a neighbourhood of $\hat{x}, N_{\varepsilon}\left ( \hat{x} \right )$ such that $d=x-\hat{x}, \forall x \in S \cap N_\varepsilon\left ( \hat{x} \right )$
Let $\hat{x}$ is not a local optimal solution.
Thus, there exists $\bar{x} \in S \cap N_\varepsilon \left ( \hat{x} \right )$ such that $f \left ( \bar{x} \right )< f \left ( \hat{x} \right )$
By assumption on $S \cap N_\varepsilon \left ( \hat{x} \right ),d=\left ( \bar{x}-\hat{x} \right )\in D$
By pseudoconvex of f,
$$f\left ( \hat{x} \right )>f\left ( \bar{x} \right )\Rightarrow \bigtriangledown f\left ( \hat{x} \right )^T\left ( \bar{x}-\hat{x} \right )<0$$
$\Rightarrow \bigtriangledown f\left ( \hat{x} \right) ^T d <0$
$\Rightarrow d \in F_0$
hence $F_0\cap D \neq \phi$
which is a contradiction.
Hence, $\hat{x}$ is local optimal solution.
Consider the following problem:$min \:f\left ( x\right )$ where $x \in X$ such that $g_x\left ( x\right ) \leq 0, i=1,2,...,m$
$f:X \rightarrow \mathbb{R},g_i:X \rightarrow \mathbb{R}^n$ and X is an open set in $\mathbb{R}^n$
Let $S=\left \{x:g_i\left ( x\right )\leq 0,\forall i \right \}$
Let $\hat{x} \in X$, then $M=\left \{1,2,...,m \right \}$
Let $I=\left \{i:g_i\left ( \hat{x}\right )=0, i \in M\right \}$ where I is called index set for all active constraints at $\hat{x}$
Let $J=\left \{i:g_i\left ( \hat{x}\right )<0,i \in M\right \}$ where J is called index set for all active constraints at $\hat{x}$.
Let $F_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown f\left ( \hat{x} \right )^T d <0 \right \}$
Let $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gI\left ( \hat{x} \right )^T d <0 \right \}$
or $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gi\left ( \hat{x} \right )^T d <0 ,\forall i \in I \right \}$
Lemma
If $S=\left \{ x \in X:g_i\left ( x\right ) \leq 0, \forall i \in I\right \}$ and X is non-empty open set in $\mathbb{R}^n$. Let $\hat{x}\in S$ and $g_i$ are different at $\hat{x}, i \in I$ and let $g_i$ where $i \in J$ are continuous at $\hat{x}$, then $G_0 \subseteq D$.
Proof
Let $d \in G_0$
Since $\hat{x} \in X$ and X is an open set, thus there exists $\delta_1 >0$ such that $\hat{x}+\lambda d \in X$ for $\lambda \in \left ( 0, \delta_1\right )$
Also since $g_\hat{x}<0$ and $g_i$ are continuous at $\hat{x}, \forall i \in J$, there exists $\delta_2>0$, $g_i\left ( \hat{x}+\lambda d\right )<0, \lambda \in \left ( 0, \delta_2\right )$
Since $d \in G_0$, therefore, $\bigtriangledown g_i\left ( \hat{x}\right )^T d <0, \forall i \in I$ thus there exists $\delta_3 >0, g_i\left ( \hat{x}+\lambda d\right )< g_i\left ( \hat{x}\right )=0$, for $\lambda \in \left ( 0, \delta_3\right ) i \in J$
Let $\delta=min\left \{ \delta_1, \delta_2, \delta_3 \right \}$
therefore, $\hat{x}+\lambda d \in X, g_i\left ( \hat{x}+\lambda d\right )< 0, i \in M$
$\Rightarrow \hat{x}+\lambda d \in S$
$\Rightarrow d \in D$
$\Rightarrow G_0 \subseteq D$
Hence Proved.
Theorem
Necessary Condition
Let $f$ and $g_i, i \in I$, are different at $\hat{x} \in S,$ and $g_j$ are continous at $\hat{x} \in S$. If $\hat{x}$ is local minima of $S$, then $F_0 \cap G_0=\phi$.
Sufficient Condition
If $F_0 \cap G_0= \phi$ and f is a pseudoconvex function at $\left (\hat{x}, g_i 9x \right ), i \in I$ are strictly pseudoconvex functions over some $\varepsilon$ - neighbourhood of $\hat{x}, \hat{x}$ is a local optimal solution.
비고
허락하다 $\hat{x}$ 실현 가능한 지점이 $\bigtriangledown f\left(\hat{x} \right)=0$, 다음 $F_0 = \phi$. 그러므로,$F_0 \cap G_0= \phi$ 그러나 $\hat{x}$ 최적의 솔루션이 아닙니다
그러나 만약 $\bigtriangledown g\left(\hat{x} \right)=0$, 다음 $G_0=\phi$, 따라서 $F_0 \cap G_0= \phi$
문제 고려 : 분 $f\left(x \right)$ 그런 $g\left(x \right)=0$.
이후 $g\left(x \right)=0$따라서 $ g_1 \ left (x \ right) = g \ left (x \ right) <0 $ 및 $g_2\left(x \right)=-g\left(x \right) \leq 0$.
허락하다 $\hat{x} \in S$, 다음 $g_1\left(\hat{x} \right)=0$ 과 $g_2\left(\hat{x} \right)=0$.
그러나 $\bigtriangledown g_1\left(\hat{x} \right)= - \bigtriangledown g_2\left(\hat{x}\right)$
그러므로, $G_0= \phi$ 과 $F_0 \cap G_0= \phi$.
필요한 조건
정리
문제를 고려하십시오- $min f\left ( x \right )$ 그런 $x \in X$ 여기서 X는 열린 집합입니다. $\mathbb{R}^n$ 그리고하자 $g_i \left ( x \right ) \leq 0, \forall i =1,2,....m$.
허락하다 $f:X \rightarrow \mathbb{R}$ 과 $g_i:X \rightarrow \mathbb{R}$
허락하다 $\hat{x}$ 가능한 해결책이되고 f와 $g_i, i \in I$ 차별화 가능 $\hat{x}$ 과 $g_i, i \in J$ 연속적이다 $\hat{x}$.
만약 $\hat{x}$ 위의 문제를 로컬로 해결하면 $u_0, u_i \in \mathbb{R}, i \in I$ 그런 $u_0 \bigtriangledown f\left ( \hat{x} \right )+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i \left ( \hat{x} \right )$= 0
어디 $u_0,u_i \geq 0,i \in I$ 과 $\left ( u_0, u_I \right ) \neq \left ( 0,0 \right )$
또한 $g_i,i \in J$ 또한 $\hat{x}$, 위의 조건은 다음과 같이 쓸 수 있습니다-
$u_0 \bigtriangledown f\left ( \hat{x}\right )+\displaystyle\sum\limits_{i=1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right )=0$
$u_ig_i\left (\hat{x} \right )$= 0
$u_0,u_i \geq 0, \forall i=1,2,....,m$
$\left (u_0,u \right ) \neq \left ( 0,0 \right ), u=\left ( u_1,u_2,s,u_m \right ) \in \mathbb{R}^m$
비고
$u_i$ 라그랑주 승수라고합니다.
조건 $\hat{x}$ 주어진 문제에 대해 실현 가능하다는 것을 원시 실현 가능 조건이라고합니다.
요구 사항 $u_0 \bigtriangledown f\left (\hat{x} \right )+\displaystyle\sum\limits_{i=1}^m u-i \bigtriangledown g_i\left ( x \right )=0$ 이중 타당성 조건이라고합니다.
조건 $u_ig_i\left ( \hat{x} \right )=0, i=1, 2, ...m$이를 보완 여유 상태라고합니다. 이 조건은$u_i=0, i \in J$
원시 실행 가능 조건, 이중 실행 가능성 조건 및 보완 여유를 함께 사용하여 프리츠-존 조건이라고합니다.
충분한 조건
정리
존재하는 경우 $\varepsilon$-이웃 $\hat{x}N_\varepsilon \left ( \hat{x} \right ),\varepsilon >0$ f가 위가 볼록하도록 $N_\varepsilon \left ( \hat{x} \right )\cap S$ 과 $g_i,i \in I$ 엄격히 유사 볼록 $N_\varepsilon \left ( \hat{x}\right )\cap S$, 다음 $\hat{x}$위에서 설명한 문제에 대한 로컬 최적의 솔루션입니다. f가 가상 볼록면$\hat{x}$ 그리고 만약 $g_i, i \in I$ 엄격하게 pseudoconvex 및 quasiconvex 함수입니다. $\hat{x},\hat{x}$ 위에서 설명한 문제에 대한 글로벌 최적 솔루션입니다.
예
$min \:f\left ( x_1,x_2 \right )=\left ( x_1-3 \right )^2+\left ( x_2-2 \right )^2$
그런 $x_{1}^{2}+x_{2}^{2} \leq 5, x_1+2x_2 \leq 4, x_1,x_2 \geq 0$ 과 $\hat{x}=\left ( 2,1 \right )$
허락하다 $g_1\left (x_1,x_2 \right )=x_{1}^{2}+x_{2}^{2} -5,$
$g_2\left (x_1,x_2 \right )=x_1+2x_2-4,$
$g_3\left (x_1,x_2 \right )=-x_1$ 과 $g_4\left ( x_1, x_2 \right )= -x_2$.
따라서 위의 제약 조건은 다음과 같이 작성할 수 있습니다.
$g_1\left (x_1,x_2 \right )\leq 0,$
$g_2\left (x_1,x_2 \right )\leq 0,$
$g_3\left (x_1,x_2 \right )\leq 0$ 과
$g_4\left (x_1,x_2 \right )\leq 0$ 그러므로, $I = \left \{1,2 \right \}$ 따라서, $u_3=0,u_4=0$
$\bigtriangledown f \left (\hat{x} \right )=\left (2,-2 \right ),\bigtriangledown g_1\left (\hat{x} \right )=\left (4,2 \right )$ 과 $\bigtriangledown g_2\left (\hat{x} \right )=\left (1,2 \right )$
따라서 이러한 값을 Fritz-John 조건의 첫 번째 조건에 넣으면 다음과 같이됩니다.
$u_0=\frac{3}{2} u_2, \:\:u_1= \frac{1}{2}u_2,$ 그리고하자 $u_2=1$따라서 $u_0= \frac{3}{2},\:\:u_1= \frac{1}{2}$
따라서 Fritz John 조건이 충족됩니다.
$min f\left (x_1,x_2\right )=-x_1$.
그런 $x_2-\left (1-x_1\right )^3 \leq 0$,
$-x_2 \leq 0$ 과 $\hat{x}=\left (1,0\right )$
허락하다 $g_1\left (x_1,x_2 \right )=x_2-\left (1-x_1\right )^3$,
$g_2\left (x_1,x_2 \right )=-x_2$
따라서 위의 제약 조건은 다음과 같이 작성할 수 있습니다.
$g_1\left (x_1,x_2 \right )\leq 0,$
$g_2\left (x_1,x_2 \right )\leq 0,$
그러므로, $I=\left \{1,2 \right \}$
$\bigtriangledown f\left (\hat{x} \right )=\left (-1,0\right )$
$\bigtriangledown g_1 \left (\hat{x} \right )=\left (0,1\right )$ 과 $g_2 \left (\hat{x} \right )=\left (0, -1 \right )$
따라서 이러한 값을 Fritz-John 조건의 첫 번째 조건에 넣으면 다음과 같이됩니다.
$u_0=0,\:\: u_1=u_2=a>0$
따라서 Fritz John 조건이 충족됩니다.
문제를 고려하십시오-
$min \:f\left ( x \right )$ 그런 $x \in X$, 여기서 X는 $\mathbb{R}^n$ 과 $g_i \left ( x \right )\leq 0, i=1, 2,...,m$
허락하다 $S=\left \{ x \in X:g_i\left ( x \right )\leq 0, \forall i \right \}$
허락하다 $\hat{x} \in S$ 그리고하자 $f$ 과 $g_i,i \in I$ 차별화 가능 $\hat{x}$ 과 $g_i, i \in J$ 연속적이다 $\hat{x}$. 더욱이,$\bigtriangledown g_i\left ( \hat{x} \right), i \in I$선형 적으로 독립적입니다. 만약$\hat{x}$ 위의 문제를 로컬로 해결하면 $u_i,i \in I$ 그런
$\bigtriangledown f\left ( x\right)+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$, $\:\:u_i \geq 0, i \in I$
만약 $g_i,i \in J$ 또한 $\hat{x}$. 그때$\hat{x}$, 다음
$\bigtriangledown f\left ( \hat{x}\right)+\displaystyle\sum\limits_{i= 1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$
$u_ig_i\left ( \hat{x} \right)=0, \forall i=1,2,...,m$
$u_i \geq 0 \forall i=1,2,...,m$
예
다음 문제를 고려하십시오-
$min \:f\left ( x_1,x_2 \right )=\left ( x_1-3\right )^2+\left ( x_2-2\right )^2$
그런 $x_{1}^{2}+x_{2}^{2}\leq 5$,
$x_1,2x_2 \geq 0$ 과 $\hat{x}=\left ( 2,1 \right )$
허락하다 $g_1\left ( x_1, x_2 \right)=x_{1}^{2}+x_{2}^{2}-5$,
$g_2\left ( x_1, x_2 \right)=x_{1}+2x_2-4$
$g_3\left ( x_1, x_2 \right)=-x_{1}$ 과 $g_4\left ( x_1,x_2 \right )=-x_2$
따라서 위의 제약 조건은 다음과 같이 작성할 수 있습니다.
$g_1 \left ( x_1,x_2 \right)\leq 0, g_2 \left ( x_1,x_2 \right) \leq 0$
$g_3 \left ( x_1,x_2 \right)\leq 0,$ 과 $g_4 \left ( x_1,x_2 \right) \leq 0$ 그러므로, $I=\left \{ 1,2 \right \}$ 따라서, $ u_3=0,\:\: u_4=0$
$\bigtriangledown f \left ( \hat{x} \right)=\left ( 2,-2 \right), \bigtriangledown g_1 \left ( \hat{x} \right)= \left ( 4,2 \right)$ 과
$\bigtriangledown g_2\left ( \hat{x} \right ) =\left ( 1,2 \right )$
따라서 이러한 값을 Karush-Kuhn-Tucker 조건의 첫 번째 조건에 넣으면 다음과 같이됩니다.
$u_1=\frac{1}{3}$ 과 $u_2=\frac{2}{3}$
따라서 Karush-Kuhn-Tucker 조건이 충족됩니다.
가파른 하강 방법
이 방법은 Gradient 방법 또는 Cauchy의 방법이라고도합니다. 이 방법은 다음 용어를 포함합니다-
$$x_{k+1}=x_k+\alpha_kd_k$$
$d_k= - \bigtriangledown f\left ( x_k \right )$ 또는 $ d_k= -\frac{\bigtriangledown f\left ( x_k \right )}{\left \| \bigtriangledown f\left ( x_k \right ) \right \|}$
허락하다 $\phi \left (\alpha \right )=f\left ( x_k +\alpha d_k\right )$
차별화함으로써 $\phi$ 0과 같게하면 $\alpha$.
따라서 알고리즘은 다음과 같습니다.
초기화 $x_0$,$\varepsilon_1$,$\varepsilon_2$ 및 설정 $k=0$.
세트 $d_k=-\bigtriangledown f\left ( x_k \right ) $또는 $d_k=-\frac{\bigtriangledown f\left (x_k \right )}{\left \|\bigtriangledown f\left (x_k \right ) \right \|}$.
찾기 $\alpha_k$ 최소화하도록 $\phi\left ( \alpha \right )=f\left ( x_k+\alpha d_k \right )$.
세트 $x_{k+1}=x_k+\alpha_kd_k$.
$ \ 왼쪽 \ | x_ {k + 1-x_k} \ 오른쪽 \ | <\ varepsilon_1 $ 또는$\left \| \bigtriangledown f\left ( x_{k+1} \right ) \right \| \leq \varepsilon_2$, 6 단계로 이동하고 그렇지 않으면 설정 $k=k+1$ 2 단계로 이동합니다.
최적의 솔루션은 $\hat{x}=x_{k+1}$.
뉴턴 방법
뉴턴 방법은 다음과 같은 원리로 작동합니다-
$f\left ( x \right )=y\left ( x \right )=f\left ( x_k \right )+\left ( x-x_k \right )^T \bigtriangledown f\left ( x_k \right )+\frac{1}{2}\left ( x-x_k \right )^T H\left ( x_k \right )\left ( x-x_k \right )$
$\bigtriangledown y\left ( x \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x-x_k \right )$
에서 $x_{k+1}, \bigtriangledown y\left ( x_{k+1} \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x_{k+1}-x_k \right )$
에 대한 $x_{k+1}$ 최적의 솔루션 $\bigtriangledown y\left ( x_k+1 \right )=0$
그러므로, $x_{k+1}=x_k-H\left ( x_k \right )^{-1} \bigtriangledown f\left ( x_k \right )$
여기 $H\left ( x_k \right )$ 단수가 아니어야합니다.
따라서 알고리즘은 다음과 같습니다.
Step 1 − 초기화 $x_0,\varepsilon$ 및 설정 $k=0$.
Step 2 − 찾기 $H\left ( x_k \right ) \bigtriangledown f\left ( x_k \right )$.
Step 3 − 선형 시스템 풀기 $H\left ( x_k \right )h\left ( x_k \right )=\bigtriangledown f\left ( x_k \right )$ ...에 대한 $h\left ( x_k \right )$.
Step 4 − 찾기 $x_{k+1}=x_k-h\left ( x_k \right )$.
Step 5− $ \ left \ | x_ {k + 1} -x_k \ right \ | <\ varepsilon $ 또는$\left \| \bigtriangledown f\left ( x_k \right ) \right \| \leq \varepsilon$ 그런 다음 6 단계로 이동하고 그렇지 않으면 $k=k+1$ 2 단계로 이동합니다.
Step 6 − 최적의 솔루션은 $\hat{x}=x_{k+1}$.
켤레 기울기 방법
이 방법은 다음 유형의 문제를 해결하는 데 사용됩니다.
$min f\left ( x \right )=\frac{1}{2}x^T Qx-bx$
여기서 Q는 양의 정부 호 nXn 행렬이고 b는 상수입니다.
주어진 $x_0,\varepsilon,$ 계산하다 $g_0=Qx_0-b$
세트 $d_0=-g_0$ ...에 대한 $k=0,1,2,...,$
세트 $\alpha_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Q d_k}$
계산 $x_{k+1}=x_k+\alpha_kd_k$
세트 $g_{k+1}=g_k+\alpha_kd_k$
계산 $\beta_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Qd_k}$
계산 $x_{k+1}=x_k+\alpha_kd_k$
세트 $g_{k+1}=x_k+\alpha_kQd_k$
계산 $\beta_k=\frac{g_{k+1}^{T}g_{k+1}}{g_{k}^{T}gk}$
세트 $d_{k+1}=-g_{k+1}+\beta_kd_k$.