전기 수량 구분 원칙
이 장에서는 전기량의 다음 두 가지 분할 원칙에 대해 논의하겠습니다.
- 현재 분할 원칙
- 전압 분할 원리
현재 분할 원칙
두 개 이상의 수동 소자가 병렬로 연결되면 각 소자를 통해 흐르는 전류의 양이 divided (공유) 노드에 들어가는 전류에서 그들 사이.
다음을 고려하세요 circuit diagram.
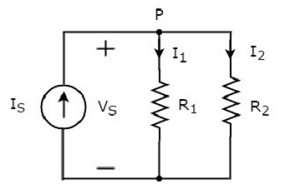
위의 회로도는 입력 전류 소스로 구성됩니다. IS 두 개의 저항기와 병렬로 R1 과 R2. 각 요소의 전압은VS. 저항을 통해 흐르는 전류R1 과 R2 아르 I1 과 I2 각기.
그만큼 KCL equation 노드에서 P 될거야
$$ I_S = I_1 + I_2 $$
위 방정식에서 $ I_1 = \ frac {V_S} {R_1} $ 및 $ I_2 = \ frac {V_S} {R_2} $를 대체합니다.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} = V_S \ lgroup \ frac {R_2 + R_1} {R_1 R_2} \ rgroup $$
$$ \ 오른쪽 화살표 V_S = I_S \ lgroup \ frac {R_1R_2} {R_1 + R_2} \ rgroup $$
$ I_1 = \ frac {V_S} {R_1} $에서 V S 값을 대체합니다 .
$$ I_1 = \ frac {I_S} {R_1} \ l 그룹 \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ 오른쪽 화살표 I_1 = I_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
$ I_2 = \ frac {V_S} {R_2} $에서 V S 값을 대체합니다 .
$$ I_2 = \ frac {I_S} {R_2} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ 오른쪽 화살표 I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
I 1 과 I 2의 방정식 에서 다음 공식을 사용하여 수동 소자를 통해 흐르는 전류를 찾을 수 있음을 일반화 할 수 있습니다.
$$ I_N = I_S \ lgroup \ frac {Z_1 \ rVert Z_2 \ rVert ... \ rVert Z_ {N-1}} {Z_1 + Z_2 + ... + Z_N} \ rgroup $$
이것은 current division principle 두 개 이상의 수동 소자가 병렬로 연결되고 하나의 전류 만 노드에 유입 될 때 적용됩니다.
어디,
I N 은 N 번째 분기 의 수동 소자를 통해 흐르는 전류 입니다.
I S 는 노드에 들어가는 입력 전류입니다.
Z 1 , Z 2 ,…, Z N 은 각각 첫 번째 분기, 두 번째 분기,…, N 번째 분기 의 임피던스입니다 .
전압 분할 원리
두 개 이상의 수동 소자가 직렬로 연결되면 각 소자에 존재하는 전압의 양은 divided (공유) 전체 조합에서 사용할 수있는 전압에서
다음을 고려하세요 circuit diagram.
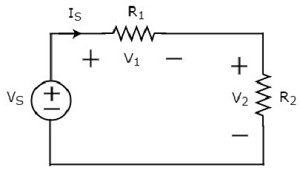
위의 회로도는 두 개의 저항 R 1 및 R 2 와 직렬로 연결된 전압 소스 V S 로 구성됩니다 . 이러한 요소를 통해 흐르는 전류는 I S 입니다. 저항 R 1 및 R 2 양단의 전압 강하 는 각각 V 1 및 V 2 입니다.
그만큼 KVL equation 루프 주위는
$$ V_S = V_1 + V_2 $$
위 방정식에서 V 1 = I S R 1 및 V 2 = I S R 2 를 대체합니다.
$$ V_S = I_S R_1 + I_S R_2 = I_S (R_1 + R_2) $$
$$ I_S = \ frac {V_S} {R_1 + R_2} $$
값의 대체 I S를 로 V 1 = I S R 1 .
$$ V_1 = \ l 그룹 \ frac {V_S} {R_1 + R_2} \ r 그룹 R_1 $$
$$ \ 오른쪽 화살표 V_1 = V_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
값의 대체 I S를 로 V 2 = I S R 2 .
$$ V_2 = \ l 그룹 \ frac {V_S} {R_1 + R_2} \ r 그룹 R_2 $$
$$ \ 오른쪽 화살표 V_2 = V_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
V 1 및 V 2 방정식 에서 다음 공식을 사용하여 수동 소자의 전압을 찾을 수 있음을 일반화 할 수 있습니다.
$$ V_N = V_S \ lgroup \ frac {Z_N} {Z_1 + Z_2 + .... + Z_N} \ rgroup $$
이것은 voltage division principle 두 개 이상의 수동 소자가 직렬로 연결되고 전체 조합에서 하나의 전압 만 사용 가능한 경우에 적용됩니다.
어디,
V N 은 N 번째 수동 소자 의 전압 입니다.
V S 는 직렬 수동 소자의 전체 조합에 존재하는 입력 전압입니다.
Z 1 , Z 2 , ..., Z (3) (1 개)의 임피던스이다 명세서 수동 소자, 2 차 수동 소자, ..., N 번째 , 각각의 수동 소자.