네트워크 이론-병렬 공명
이전 장에서 직렬 공진의 중요성에 대해 논의했습니다. 이제 RLC 회로의 병렬 공진에 대해 설명하겠습니다.
병렬 공진 회로도
병렬 RLC 회로에서 공진이 발생하면 다음과 같이 호출됩니다. Parallel Resonance. 다음을 고려하세요parallel RLC circuit, 이는 페이저 도메인으로 표시됩니다.
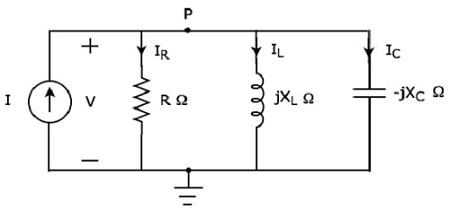
여기서 저항, 인덕터 및 커패시터와 같은 수동 소자는 병렬로 연결됩니다. 이 전체 조합은parallel 입력 정현파 전류 소스로.
쓰다 nodal equation 노드 P에서.
$$-I + I_R + I_L + I_C = 0 $$
$$ \ 오른쪽 화살표-I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {-j X_C} = 0 $$
$$ \ 오른쪽 화살표 I = \ frac {V} {R}-\ frac {jV} {X_L} + \ frac {jV} {X_C} $$
$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C}-\ frac {1} {X_L} \ rgroup] $Equation 1
위의 방정식은 다음과 같습니다. I = VY.
따라서 admittance Y 병렬 RLC 회로의
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C}-\ frac {1} {X_L} \ rgroup $$
공명시 매개 변수 및 전기적 양
이제 병렬 RLC 회로의 공진에서 매개 변수와 전기량의 값을 하나씩 유도 해 보겠습니다.
공진 주파수
우리는 resonant frequency, fr공진이 발생하는 주파수입니다. 병렬 RLC 회로 공진은 어드미턴스의 허수 항 Y가 0 일 때 발생합니다. 즉, $ \ frac {1} {X_C}-\ frac {1} {X_L} $의 값은 0과 같아야합니다.
$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$
$$ \ 오른쪽 화살표 X_L = X_C $$
위의 공진 조건은 직렬 RLC 회로와 동일합니다. 그래서resonant frequency, fr 직렬 RLC 회로와 병렬 RLC 회로 모두에서 동일합니다.
따라서 resonant frequency, fr 병렬 RLC 회로의
$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$
어디,
- L은 인덕터의 인덕턴스입니다.
- C는 커패시터의 커패시턴스입니다.
그만큼 resonant frequency, fr 병렬 RLC 회로의 수는 인덕턴스에만 의존합니다. L 및 커패시턴스 C. 하지만 저항과는 무관하다R.
입장
우리는 admittance Y 병렬 RLC 회로의
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C}-\ frac {1} {X_L} \ rgroup $$
위 방정식에서 $ X_L = X_C $를 대입합니다.
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C}-\ frac {1} {X_C} \ rgroup $$
$$ \ 오른쪽 화살표 Y = \ frac {1} {R} + j (0) $$
$$ \ 오른쪽 화살표 Y = \ frac {1} {R} $$
공명에서 admittance, 병렬 RLC 회로의 Y는 저항 R의 역수와 같습니다. 즉, $ \ mathbf {\ mathit {Y = \ frac {1} {R}}} $
각 요소의 전압
방정식 1에서 $ \ frac {1} {X_C}-\ frac {1} {X_L} = 0 $ 대체
$$ I = V [\ frac {1} {R} + j (0)] $$
$$ \ 오른쪽 화살표 I = \ frac {V} {R} $$
$$ \ 오른쪽 화살표 V = IR $$
따라서 voltage 공진에서 병렬 RLC 회로의 모든 요소에 걸쳐 V = IR.
공진시 병렬 RLC 회로의 어드미턴스는 최소값에 도달합니다. 그 후,maximum voltage 공진시이 회로의 각 요소에 존재합니다.
저항기를 통해 흐르는 전류
저항을 통해 흐르는 전류는
$$ I_R = \ frac {V} {R} $$
가치를 대체하십시오 V 위의 방정식에서.
$$ I_R = \ frac {IR} {R} $$
$$ \ 오른쪽 화살표 I_R = I $$
따라서 current flowing through resistor 공명에서 $ \ mathbf {\ mathit {I_R = I}} $입니다.
인덕터를 통해 흐르는 전류
인덕터를 통해 흐르는 전류는
$$ I_L = \ frac {V} {j X_L} $$
가치를 대체하십시오 V 위의 방정식에서.
$$ I_L = \ frac {IR} {j X_L} $$
$$ \ 오른쪽 화살표 I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I $$
$$ \ 오른쪽 화살표 I_L = -jQI $$
따라서 current flowing through inductor 공명에서 $ I_L = -jQI $입니다.
그래서 magnitude 공진시 인덕터를 통해 흐르는 전류의
$$ | I_L | = QI $$
여기서 Q는 Quality factor 그 값은 $ \ frac {R} {X_L} $와 같습니다.
커패시터를 통해 흐르는 전류
커패시터를 통해 흐르는 전류는
$$ I_C = \ frac {V} {-j X_C} $$
가치를 대체하십시오 V 위의 방정식에서.
$$ I_C = \ frac {IR} {-j X_C} $$
$$ \ 오른쪽 화살표 I_C = j \ l 그룹 \ frac {R} {X_C} \ r 그룹 I $$
$$ \ 오른쪽 화살표 I_C = jQI $$
따라서 current flowing through capacitor 공명에서 $ I_C = jQI $
그래서 magnitude 공진시 커패시터를 통해 흐르는 전류의
$$ | I_C | = QI $$
여기서 Q는 Quality factor 그 값은 $ \ frac {R} {X_C} $와 같습니다.
Note − 병렬 공진 RLC 회로는 current magnification회로. 왜냐하면 인덕터와 커패시터를 통해 흐르는 전류의 크기 는 입력 정현파 전류 I의 Q 배 와 같기 때문 입니다.