네트워크 이론-Norton의 정리
Norton’s theoremThevenin의 정리와 유사합니다. 두 개의 터미널 선형 네트워크 또는 회로는 저항과 병렬로 전류 소스로 구성된 등가 네트워크 또는 회로로 표현 될 수 있음을 나타냅니다. 그것은Norton’s equivalent circuit. 선형 회로에는 독립 소스, 종속 소스 및 저항이 포함될 수 있습니다.
회로에 여러 개의 독립 소스, 종속 소스 및 저항이있는 경우 해당 요소의 왼쪽에있는 전체 네트워크를 다음으로 대체하여 요소의 응답을 쉽게 찾을 수 있습니다. Norton’s equivalent circuit.
그만큼 response in an element 해당 요소의 전압, 해당 요소를 통해 흐르는 전류 또는 해당 요소에서 소산 된 전력이 될 수 있습니다.
이 개념은 다음 그림에 설명되어 있습니다.
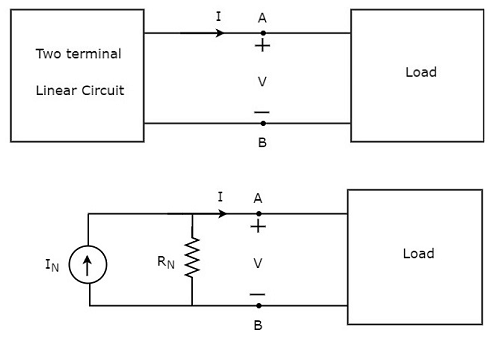
Norton’s equivalent circuit실용적인 전류 소스와 유사합니다. 따라서 저항과 병렬로 전류 소스가 있습니다.
Norton의 등가 회로에있는 전류 소스를 Norton의 등가 전류 또는 간단히 Norton’s current IN.
Norton의 등가 회로에있는 저항을 Norton의 등가 저항 또는 간단히 Norton’s resistor RN.
Norton의 등가 회로를 찾는 방법
있습니다 three methodsNorton의 등가 회로를 찾기 위해. 네트워크에있는 소스 유형에 따라이 세 가지 방법 중 하나를 선택할 수 있습니다. 이제이 세 가지 방법을 하나씩 살펴 보겠습니다.
방법 1
Norton의 등가 회로를 찾으려면 다음 단계를 따르십시오. sources of independent type 있습니다.
Step 1 − Norton의 등가 회로를 찾을 터미널을 열어 회로도를 고려하십시오.
Step 2 − Norton의 현재 찾기 IN 위 회로의 두 개의 열린 단자를 단락하여.
Step 3 − 노턴의 저항 찾기 RN회로에 존재하는 독립적 인 소스를 제거하여 1 단계에서 고려한 회로의 개방 단자에 걸쳐 있습니다. 노턴의 저항RN Thevenin의 저항과 동일합니다 RTh.
Step 4 − 그리기 Norton’s equivalent circuitNorton의 전류 IN을 Norton의 저항 R N 과 병렬로 연결하여 .
이제 Norton의 등가 회로 오른쪽에있는 요소에서 응답을 찾을 수 있습니다.
방법 2
Norton의 등가 회로를 찾으려면 다음 단계를 따르십시오. sources of both independent type and dependent type 있습니다.
Step 1 − Norton의 등가 회로를 찾을 터미널을 열어 회로도를 고려하십시오.
Step 2 − 개방 회로 전압 찾기 VOC 위 회로의 개방 단자에 걸쳐.
Step 3 − Norton의 현재 찾기 IN 위 회로의 두 개의 열린 단자를 단락하여.
Step 4 − 노턴의 저항 찾기 RN 다음 공식을 사용하여.
$$ R_N = \ frac {V_ {OC}} {I_N} $$
Step 5− Norton의 전류 I N 을 Norton의 저항 R N 과 병렬로 연결하여 Norton의 등가 회로를 그 립니다.
이제 Norton의 등가 회로 오른쪽에있는 요소에서 응답을 찾을 수 있습니다.
방법 3
이것은 Norton의 등가 회로를 찾는 대체 방법입니다.
Step 1 − 찾기 Thevenin’s equivalent circuit원하는 두 터미널 사이. 우리는 그것이 Thevenin의 전압 소스, V Th 및 Thevenin의 저항 R Th 로 구성된다는 것을 알고 있습니다 .
Step 2 − 적용 source transformation technique위의 Thevenin의 등가 회로에. Norton의 등가 회로를 얻을 것입니다. 여기,
Norton의 현재,
$$ I_N = \ frac {V_ {Th}} {R_ {Th}} $$
노턴의 저항,
$$ R_N = R_ {Th} $$
이 개념은 다음 그림에 설명되어 있습니다.
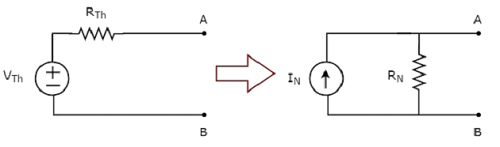
이제 Norton의 등가 회로를 해당 요소의 왼쪽에 배치하여 요소에서 응답을 찾을 수 있습니다.
Note− 마찬가지로 Norton의 등가 회로를 먼저 찾은 다음 소스 변환 기술을 적용하여 Thevenin의 등가 회로를 찾을 수 있습니다. 이 개념은 다음 그림에 설명되어 있습니다.
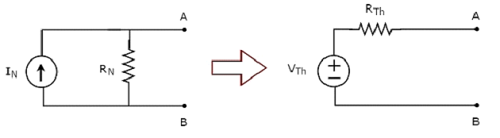
이것은 Thevenin의 등가 회로를 찾는 방법 3입니다.
예
먼저 20Ω 저항을 통해 흐르는 전류를 찾습니다. Norton’s equivalent circuit 터미널 A와 B의 왼쪽에 있습니다.
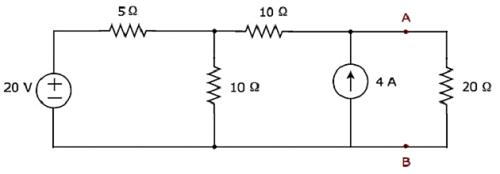
이 문제를 Method 3.
Step 1− 이전 장에서 터미널 A와 B의 왼쪽에있는 Thevenin의 등가 회로를 계산했습니다. 이제이 회로를 사용할 수 있습니다. 다음 그림에 나와 있습니다.
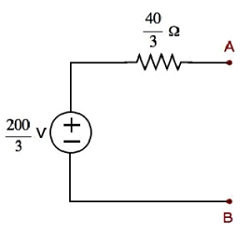
여기에서 Thevenin의 전압, $ V_ {Th} = \ frac {200} {3} V $ 및 Thevenin의 저항, $ R_ {Th} = \ frac {40} {3} \ Omega $
Step 2 − 적용 source transformation technique위의 Thevenin의 등가 회로에. 다음 공식에서 V Th 및 R Th 값을 대체하십시오.Norton’s current.
$$ I_N = \ frac {V_ {Th}} {R_ {Th}} $$
$$ I_N = \ frac {\ frac {200} {3}} {\ frac {40} {3}} = 5A $$
따라서 Norton의 현재 I N 은5 A.
우리는 노턴의 저항, 알고 R N은 테브난의 저항과 동일 R 목 .
$$ \ mathbf {R_N = \ frac {40} {3} \ Omega} $$
위의 Thevenin 등가 회로에 해당하는 Norton의 등가 회로는 다음 그림에 나와 있습니다.
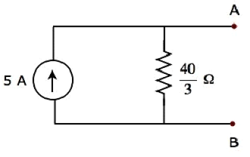
이제 Norton의 등가 회로를 주어진 회로의 터미널 A 및 B 왼쪽에 배치하십시오.
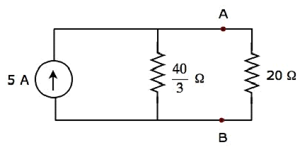
사용하여 current division principle, 20Ω 저항을 통해 흐르는 전류는
$$ I_ {20 \ Omega} = 5 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup $$
$$ I_ {20 \ Omega} = 5 \ lgroup \ frac {40} {100} \ rgroup = 2A $$
따라서 20Ω 저항을 통해 흐르는 전류는 2 A.