네트워크 이론-DC 회로의 응답
입력에 대한 전기 회로의 출력이 시간에 따라 변하면 다음과 같이 호출됩니다. time response. 시간 응답은 다음 두 부분으로 구성됩니다.
- 과도 응답
- 정상 상태 응답
이 장에서는 먼저이 두 응답에 대해 논의한 다음 DC 전압 소스에 의해 여기 될 때 직렬 RL 회로에서이 두 응답을 관찰합니다.
과도 응답
전기 회로에 입력을 적용한 후 출력이 정상 상태에 도달하는 데 일정 시간이 걸립니다. 따라서 출력은 정상 상태가 될 때까지 일시적인 상태가됩니다. 따라서 과도 상태에서 전기 회로의 응답은 다음과 같이 알려져 있습니다.transient response.
과도 응답은 't'값이 큰 경우 0이됩니다. 이상적으로는이 't'값은 무한대 여야합니다. 그러나 실제로five time constants 충분합니다.
과도 상태의 존재 또는 부재
응답에서 과도 현상이 발생하는 이유는 sudden change전기 회로에 적용되는 소스 및 / 또는 스위칭 동작으로 인해. 두 가지 가능한 전환 동작이 있습니다. 그것들은 개폐 스위치입니다.
그만큼 transient 부분은 not present저항 만 포함하는 경우 전기 회로 또는 네트워크의 응답으로. 때문에resistor 모든 양의 전압과 전류를 조정할 수 있습니다.
그만큼 transient part occurs 다음과 같은 에너지 저장 요소의 존재로 인해 전기 회로 또는 네트워크의 응답으로 inductor and capacitor. 그 요소에 저장된 에너지를 즉시 변경할 수 없기 때문입니다.
인덕터 동작
스위칭 동작이 t = 0 에서 발생한다고 가정합니다 .Inductor current전환 동작이 발생할 때 즉시 변경되지 않습니다. 즉, 스위칭 동작 직후의 인덕터 전류 값은 스위칭 동작 직전의 값과 동일합니다.
수학적으로 다음과 같이 나타낼 수 있습니다.
$$ i_L (0 ^ +) = i_L (0 ^-) $$
커패시터 동작
그만큼 capacitor voltage스위칭 동작이 발생할 때 인덕터 전류와 유사하게 순간적으로 변하지 않습니다. 즉, 스위칭 동작 직후의 커패시터 전압 값은 스위칭 동작 직전의 값과 동일합니다.
수학적으로 다음과 같이 나타낼 수 있습니다.
$$ v_c (0 ^ +) = v_c (0 ^-) $$
정상 상태 응답
과도 응답이 큰 't'값에 대해 0 값이 된 후에도 남아있는 시간 응답 부분은 다음과 같이 알려져 있습니다. steady state response. 이는 정상 상태 동안 응답에 일시적인 부분이 없음을 의미합니다.
인덕터 동작
독립 소스가 하나 이상의 인덕터 및 저항 (옵션)이있는 전기 회로 또는 네트워크에 장시간 연결되면 해당 전기 회로 또는 네트워크는 정상 상태라고합니다. 따라서 해당 전기 회로의 인덕터 (들)에 저장된 에너지는 최대이며 일정합니다.
수학적으로 다음과 같이 나타낼 수 있습니다.
$ W_L = \ frac {L {i_L} ^ 2} {2} = $ 최대 및 상수
$ \ Rightarrow i_L = $ 최대 및 상수
따라서 인덕터는 constant current source 정상 상태에서.
인덕터 양단의 전압은
$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$
따라서 인덕터는 short circuit 정상 상태에서.
커패시터 동작
독립 소스가 하나 이상의 커패시터와 저항 (선택 사항)이있는 전기 회로 또는 네트워크에 장시간 연결되면 해당 전기 회로 또는 네트워크가 정상 상태에 있다고합니다. 따라서 해당 전기 회로의 커패시터 (들)에 저장된 에너지는 최대이며 일정합니다.
수학적으로 다음과 같이 나타낼 수 있습니다.
$ W_c = \ frac {C {v_c} ^ 2} {2} = $ 최대 및 상수
$ \ Rightarrow v_c = $ 최대 및 상수
따라서 커패시터는 constant voltage source 정상 상태에서.
커패시터를 통해 흐르는 전류는
$$ i_c = C \ frac {dv_c} {dt} = 0A $$
따라서 커패시터는 open circuit 정상 상태에서.
직렬 RL 회로의 응답 찾기
다음을 고려하세요 series RL circuit 도표.
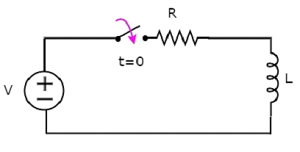
위의 회로에서 switch 보관되었다 open최대 t = 0이고 t = 0에서 닫혔습니다. 따라서 V 볼트를 갖는 DC 전압 소스는 지금까지 직렬 RL 회로에 연결되지 않았습니다. 따라서no initial current 인덕터를 통해 흐릅니다.
회로도, 때 switch 에 closed 위치는 다음 그림에 나와 있습니다.
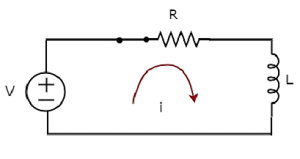
자, 현재 i DC 전압 소스는 V 볼트는 직렬 RL 회로에 연결됩니다.
이제 신청하세요 KVL 루프 주위.
$$ V = Ri + L \ frac {di} {dt} $$
$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1
위의 방정식은 1 차 미분 방정식이며 다음과 같은 형태입니다.
$ \ frac {dy} {dt} + Py = Q $Equation 2
으로 comparing 방정식 1과 방정식 2, 우리는 다음과 같은 관계를 얻을 것입니다.
$$ x = t $$
$$ y = i $$
$$ P = \ frac {R} {L} $$
$$ Q = \ frac {V} {L} $$
그만큼 solution 방정식 2의
$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3
어디, k 상수입니다.
방정식 3에서 x, y, P & Q 값을 대입합니다.
$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $
$ \ Rightarrow i = \ frac {V} {R} + ke ^ {-\ lgroup \ frac {R} {L} \ rgroup} t $Equation 4
우리는 회로에 초기 전류가 없다는 것을 알고 있습니다. 따라서 대체, t = 0 및 상수 값을 찾기 위해 방정식 4에서 = 0 k.
$$ 0 = \ frac {V} {R} + ke ^ {-\ lgroup \ frac {R} {L} \ rgroup (0)} $$
$$ 0 = \ frac {V} {R} + k (1) $$
$$ k =-\ frac {V} {R} $$
방정식 4에서 k 값을 대입합니다.
$$ i = \ frac {V} {R} + \ lgroup-\ frac {V} {R} \ rgroup e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} $$
$$ i = \ frac {V} {R}-\ frac {V} {R} e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} $$
따라서 current 회로를 통해 흐르는 것은
$ i =-\ frac {V} {R} e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5
따라서 직렬 RL 회로의 응답은 DC 전압 소스에 의해 여기 될 때 다음 두 가지 항을 갖습니다.
첫 번째 항 $-\ frac {V} {R} e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} $는 transient response.
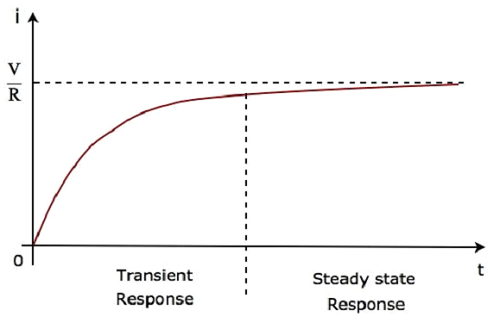
두 번째 용어 $ \ frac {V} {R} $는 steady state response. 이 두 가지 응답은 다음 그림에 나와 있습니다.
방정식 5를 다음과 같이 다시 작성할 수 있습니다.
$ i = \ frac {V} {R} \ l 그룹 1-e ^ {-\ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $
$ \ Rightarrow i = \ frac {V} {R} \ l 그룹 1-e ^ {-\ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6
어디, τ 이다 time constant 그 값은 $ \ frac {L} {R} $와 같습니다.
방정식 5와 방정식 6은 모두 동일합니다. 그러나 방정식 6에서 회로를 통해 흐르는 전류의 위 파형을 쉽게 이해할 수 있습니다.t 0, τ, 2τ, 5τ 등
회로를 통해 흐르는 위의 전류 파형에서 과도 응답은 0에서 최대 5 개의 시간 상수를 표시하는 반면, 정상 상태 응답은 5 개의 시간 상수 이후부터 표시됩니다.