네트워크 이론-중첩 정리
Superposition theorem전기 회로의 응답과 여기 사이의 선형성 개념을 기반으로합니다. 여러 독립 소스가 동시에 작동 할 때 선형 회로의 특정 분기에서의 응답은 한 번에 작동하는 각 독립 소스로 인한 응답의 합과 같습니다.
이 방법에서는 one independent source한 번에. 따라서 우리는 회로에서 남아있는 독립적 인 소스를 제거해야합니다. 두 단자를 단락시키고 마찬가지로 두 단자를 열어 전류원을 단락시킴으로써 전압원을 제거 할 수 있습니다.
따라서 특정 분기에서 응답을 찾아야합니다. ‘n’ times독립적 인 출처가 'n'인 경우. 특정 분기의 응답은 해당 분기를 통해 흐르는 전류 또는 해당 분기를 가로 지르는 전압 일 수 있습니다.
중첩 정리 절차
중첩 정리를 사용하여 특정 분기에서 응답을 찾으려면 다음 단계를 따르십시오.
Step 1 − 하나의 독립적 인 소스를 고려하고 네트워크에 존재하는 나머지 독립적 인 소스를 제거하여 특정 분기에서 응답을 찾습니다.
Step 2 − 네트워크에있는 모든 독립 소스에 대해 1 단계를 반복합니다.
Step 3 − 모든 독립적 인 소스가 네트워크에있을 때 특정 분기에서 전체 응답을 얻기 위해 모든 응답을 추가합니다.
예
다음 회로의 20Ω 저항을 통해 흐르는 전류를 찾습니다. superposition theorem.
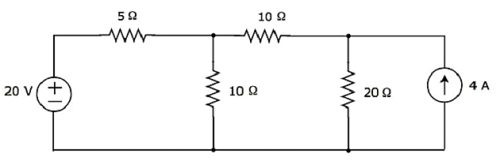
Step 1 − 20Ω 저항을 통해 흐르는 전류를 20 V voltage source. 이 경우 개방 회로를 만들어 4A 전류 소스를 제거 할 수 있습니다. 수정 된 회로도는 다음 그림에 나와 있습니다.

위의 회로에는 접지를 제외한 주 노드가 하나뿐입니다. 그래서 우리는nodal analysis방법. 노드 전압 V 1 은 다음 그림에 표시되어 있습니다. 여기서 V 1 은 접지에 대한 노드 1의 전압입니다.
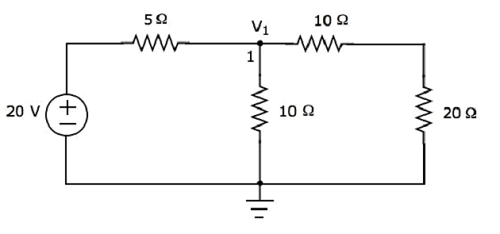
그만큼 nodal equation 노드 1에서
$$ \ frac {V_1-20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$
$$ \ Rightarrow \ frac {6V_1-120 + 3V_1 + V_1} {30} = 0 $$
$$ \ Rightarrow 10V_1 = 120 $$
$$ \ 오른쪽 화살표 V_1 = 12V $$
그만큼 current flowing through 20 Ω resistor 다음 단순화를 수행하여 찾을 수 있습니다.
$$ I_1 = \ frac {V_1} {10 + 20} $$
위의 방정식에서 V 1 의 값을 대체하십시오 .
$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0.4A $$
따라서 20Ω 저항을 통해 흐르는 전류는 0.4 A, 20V 전압 소스 만 고려할 때.
Step 2 − 20Ω 저항을 통해 흐르는 전류를 4 A current source. 이 경우 20V 전압 소스를 단락시켜 제거 할 수 있습니다. 수정 된 회로도는 다음 그림에 나와 있습니다.
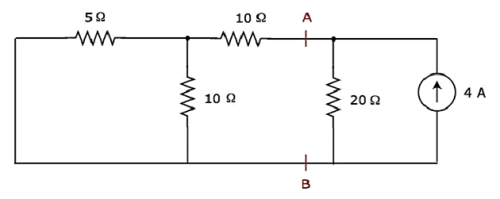
위의 회로에서 단자 A와 B의 왼쪽에 3 개의 저항이 있습니다.이 저항을 단일 저항으로 대체 할 수 있습니다. equivalent resistor. 여기에서 5Ω 및 10Ω 저항은 병렬로 연결되고 전체 조합은 10Ω 저항과 직렬로 연결됩니다.
그만큼 equivalent resistance 터미널 A와 B의 왼쪽에
$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
단순화 된 회로도는 다음 그림에 나와 있습니다.
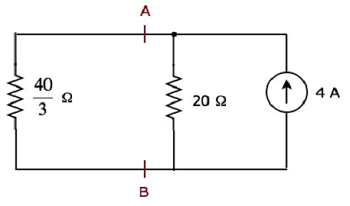
20Ω 저항을 통해 흐르는 전류를 찾을 수 있습니다. current division principle.
$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
위 방정식에서 $ I_S = 4A, \ : R_1 = \ frac {40} {3} \ Omega $ 및 $ R_2 = 20 \ Omega $를 대체합니다.
$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1.6A $$
따라서 20Ω 저항을 통해 흐르는 전류는 1.6 A, 4A 전류 소스 만 고려할 때.
Step 3 − 주어진 회로의 20Ω 저항을 통해 흐르는 전류를 얻을 수 있습니다. addition of two currents 1 단계와 2 단계에서 얻었습니다. 수학적으로 다음과 같이 쓸 수 있습니다.
$$ I = I_1 + I_2 $$
위 방정식에서 I 1 과 I 2 의 값을 대입합니다.
$$ I = 0.4 + 1.6 = 2A $$
따라서 주어진 회로의 20Ω 저항을 통해 흐르는 전류는 2 A.
Note − 우리는 양을 찾기 위해 중첩 정리를 직접 적용 할 수 없습니다. power각 독립 소스로 인해 해당 저항에 전달되는 전력을 추가하여 선형 회로에있는 모든 저항에 전달됩니다. 오히려 중첩 정리를 사용하여 해당 저항을 통과하는 총 전류 또는 전압을 계산할 수 있으며, 그로부터 $ I ^ 2 R $ 또는 $ \ frac {V ^ 2}를 사용하여 해당 저항에 전달되는 전력량을 계산할 수 있습니다. {R} $.