네트워크 이론-2 포트 네트워크
일반적으로 입력 변수와 출력 변수 사이의 관계를 제공하는 동등한 모델로 표현하면 모든 전기 네트워크를 분석하기 쉽습니다. 이를 위해 우리는two port network표현. 이름에서 알 수 있듯이 두 개의 포트 네트워크에는 두 개의 포트가 있습니다. 이 중 한 포트는 입력 포트로 사용되고 다른 포트는 출력 포트로 사용됩니다. 첫 번째 및 두 번째 포트는 각각 port1 및 port2라고합니다.
One port network전류가 한 터미널을 통해 들어오고 다른 터미널을 통해 나가는 두 터미널 전기 네트워크입니다. 저항기, 인덕터 및 커패시터는 각각 두 개의 단자가 있기 때문에 하나의 포트 네트워크의 예입니다. 다음 그림에는 하나의 포트 네트워크 표현이 나와 있습니다.
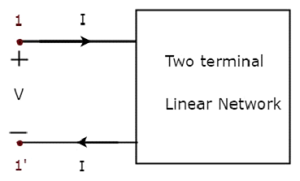
여기서 한 쌍의 터미널 1 & 1 '은 포트를 나타냅니다. 이 경우 하나의 포트 네트워크이므로 하나의 포트만 사용합니다.
비슷하게, two port network전류가 한 터미널을 통해 들어오고 각 포트의 다른 터미널을 통해 나가는 두 개의 터미널 전기 네트워크 쌍입니다. 다음 그림에는 두 개의 포트 네트워크 표시가 나와 있습니다.
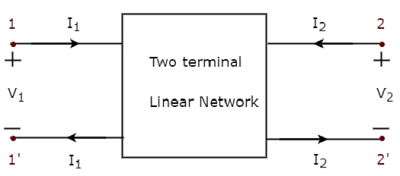
여기에서 한 쌍의 터미널, 1 & 1 '은 하나의 포트를 나타내며, port1 다른 한 쌍의 터미널, 2 & 2 '는 다른 포트를 나타냅니다. port2.
있습니다 four variables그림에 표시된대로 2 포트 네트워크에서 V 1 , V 2 , I 1 및 I 2 그 중에서 두 개의 변수를 독립으로 선택하고 다른 두 개의 변수를 종속으로 선택할 수 있습니다. 그래서 우리는 6 개의 가능한 방정식 쌍을 얻을 것입니다. 이 방정식은 독립 변수 측면에서 종속 변수를 나타냅니다. 독립 변수의 계수는 다음과 같이 불립니다.parameters. 따라서 각 방정식 쌍은 4 개의 매개 변수 세트를 제공합니다.
2 개의 포트 네트워크 매개 변수
2 포트 네트워크의 매개 변수는 다음과 같이 호출됩니다. two port network parameters또는 간단히 두 개의 포트 매개 변수입니다. 다음은 두 가지 포트 네트워크 매개 변수의 유형입니다.
- Z 매개 변수
- Y 매개 변수
- T 매개 변수
- T '매개 변수
- h-parameters
- g-parameters
이제이 두 포트 네트워크 매개 변수에 대해 하나씩 설명하겠습니다.
Z 매개 변수
변수 V 1 & V 2 를 종속으로, I 1 & I 2 를 독립 으로 간주하여 다음 두 방정식 세트를 얻습니다 . 독립 변수의 계수 I 1 및 I 2 는 다음과 같이 호출됩니다.Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
그만큼 Z parameters 아르
$$Z_{11} = \frac{V_1}{I_1}, \: when \: I_2 = 0$$
$$Z_{12} = \frac{V_1}{I_2}, \: when \: I_1 = 0$$
$$Z_{21} = \frac{V_2}{I_1}, \: when \: I_2 = 0$$
$$Z_{22} = \frac{V_2}{I_2}, \: when \: I_1 = 0$$
Z 매개 변수는 다음과 같이 호출됩니다. impedance parameters이것은 단순히 전압과 전류의 비율이기 때문입니다. Z 매개 변수의 단위는 옴 (Ω)입니다.
포트 2의 개방 회로를 수행 하여 두 개의 Z 매개 변수 Z 11 및 Z 21을 계산할 수 있습니다 . 마찬가지로 포트 1의 개방 회로를 수행 하여 다른 두 Z 매개 변수 Z 12 및 Z 22 를 계산할 수 있습니다 . 따라서 Z 매개 변수는 다음과 같이 호출됩니다.open-circuit impedance parameters.
Y 매개 변수
변수 I 1 & I 2 를 종속으로, V 1 & V 2 를 독립 으로 간주하여 다음 두 방정식 세트를 얻습니다 . 독립 변수 V 1 및 V 2 의 계수는 다음 과 같이 호출됩니다.Y parameters.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
그만큼 Y parameters 아르
$$Y_{11} = \frac{I_1}{V_1}, \: when \: V_2 = 0$$
$$Y_{12} = \frac{I_1}{V_2}, \: when \: V_1 = 0$$
$$Y_{21} = \frac{I_2}{V_1}, \: when \: V_2 = 0$$
$$Y_{22} = \frac{I_2}{V_2}, \: when \: V_1 = 0$$
Y 매개 변수는 다음과 같이 호출됩니다. admittance parameters이것은 단순히 전류와 전압의 비율이기 때문입니다. Y 매개 변수의 단위는 mho입니다.
포트 2를 단락하여 Y 매개 변수 Y 11 과 Y 21 을 계산할 수 있습니다 . 마찬가지로 포트 1의 단락을 수행 하여 다른 두 Y 매개 변수 Y 12 및 Y 22 를 계산할 수 있습니다 . 따라서 Y 매개 변수는short-circuit admittance parameters.
T 매개 변수
변수 V 1 & I 1 을 종속으로, V 2 & I 2 를 독립 으로 간주하여 다음 두 방정식 세트를 얻습니다 . V 2 및 -I 2 의 계수는 다음 과 같이 호출됩니다.T parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
그만큼 T parameters 아르
$$A = \frac{V_1}{V_2}, \: when \: I_2 = 0$$
$$B = -\frac{V_1}{I_2}, \: when \: V_2 = 0$$
$$C = \frac{I_1}{V_2}, \: when \: I_2 = 0$$
$$D = -\frac{I_1}{I_2}, \: when \: V_2 = 0$$
T 매개 변수는 전송 매개 변수 또는 ABCD parameters. 매개 변수 A와 D는 치수가 적기 때문에 단위가 없습니다. 매개 변수 B와 C의 단위는 각각 ohm과 mho입니다.
포트 2의 개방 회로를 수행하여 두 개의 매개 변수 A와 C를 계산할 수 있습니다. 마찬가지로 port2를 단락시켜 다른 두 매개 변수 B와 D를 계산할 수 있습니다.
T '매개 변수
변수 V 2 & I 2 를 종속 변수 로, V 1 & I 1 변수 를 독립적 으로 고려하여 다음 두 방정식 세트를 얻습니다 . V 1 과 -I 1 의 계수는 다음 과 같이 호출됩니다.T’ parameters.
$$V_2 = A' V_1 - B' I_1$$
$$I_2 = C' V_1 - D' I_1$$
그만큼 T’ parameters 아르
$$A' = \frac{V_2}{V_1}, \: when\: I_1 = 0$$
$$B' = -\frac{V_2}{I_1}, \: when\: V_1 = 0$$
$$C' = \frac{I_2}{V_1}, \: when\: I_1 = 0$$
$$D' = -\frac{I_2}{I_1}, \: when \: V_1 = 0$$
T '매개 변수는 역 전송 매개 변수 또는 A’B’C’D’ parameters. 매개 변수 A '및 D'에는 치수가 적기 때문에 단위가 없습니다. 매개 변수의 단위 B '와 C'는 각각 Ohm과 Mho입니다.
port1의 개방 회로를 수행하여 두 개의 매개 변수 A '와 C'를 계산할 수 있습니다. 마찬가지로 port1을 단락시켜 다른 두 매개 변수 B '와 D'를 계산할 수 있습니다.
h- 파라미터
변수 V 1 & I 2 를 종속으로, I 1 & V 2 를 독립 으로 간주하여 다음 두 방정식 세트를 얻습니다 . 독립 변수의 계수 I 1 및 V 2는 다음 과 같이 호출됩니다.h-parameters.
$$V_1 = h_{11} I_1 + h_{12} V_2$$
$$I_2 = h_{21} I_1 + h_{22} V_2$$
h 매개 변수는 다음과 같습니다.
$$h_{11} = \frac{V_1}{I_1},\: when\: V_2 = 0$$
$$h_{12} = \frac{V_1}{V_2},\: when\: I_1 = 0$$
$$h_{21} = \frac{I_2}{I_1},\: when\: V_2 = 0$$
$$h_{22} = \frac{I_2}{V_2},\: when\: I_1 = 0$$
h- 파라미터는 다음과 같이 호출됩니다. hybrid parameters. 매개 변수 h 12 및 h 21 은 치수가 없기 때문에 단위가 없습니다. 매개 변수 단위 h 11 및 h 22 는 각각 Ohm 및 Mho입니다.
port2의 단락을 수행 하여 두 개의 매개 변수 h 11 및 h 21 을 계산할 수 있습니다 . 마찬가지로 포트 1의 개방 회로를 수행 하여 다른 두 매개 변수 인 h 12 및 h 22 를 계산할 수 있습니다 .
h- 파라미터 또는 하이브리드 파라미터는 트랜지스터 모델링 회로 (네트워크)에 유용합니다.
g- 매개 변수
변수 I 1 & V 2 를 종속 변수 로, V 1 & I 2 변수 를 독립적 으로 고려하여 다음 두 방정식 세트를 얻습니다 . 독립 변수의 계수, V 1 및 I 2 로 불린다g-parameters.
$$I_1 = g_{11} V_1 + g_{12} I_2$$
$$V_2 = g_{21} V_1 + g_{22} I_2$$
그만큼 g-parameters 아르
$$g_{11} = \frac{I_1}{V_1},\: when\: I_2 = 0$$
$$g_{12} = \frac{I_1}{I_2},\: when\: V_1 = 0$$
$$g_{21} = \frac{V_2}{V_1},\: when\: I_2 = 0$$
$$g_{22} = \frac{V_2}{I_2},\: when \: V_1 = 0$$
g- 파라미터는 다음과 같이 호출됩니다. inverse hybrid parameters. 매개 변수 g 12 및 g 21 은 치수가 더 작기 때문에 단위가 없습니다. 매개 변수의 단위, g 11 및 g 22 는 각각 mho 및 ohm입니다.
포트 2의 개방 회로를 수행 하여 두 개의 매개 변수 g 11 및 g 21 을 계산할 수 있습니다 . 마찬가지로 port1의 단락을 수행 하여 다른 두 매개 변수 g 12 및 g 22 를 계산할 수 있습니다 .