네트워크 이론-직렬 공명
Resonance인덕터 및 커패시터와 같은 에너지 저장 요소의 존재로 인해 전기 회로에서 발생합니다. 라디오와 TV 수신기가 원하는 방송국 주파수 만 선택할 수 있도록 설계되는 것이 기본 개념입니다.
있습니다 two types공명, 즉 직렬 공명 및 병렬 공명. 이들은 직렬 또는 병렬로 연결된 네트워크 요소에 따라 분류됩니다. 이 장에서는 직렬 공진에 대해 논의하겠습니다.
직렬 공진 회로도
직렬 RLC 회로에서 공진이 발생하면 다음과 같이 호출됩니다. Series Resonance. 다음을 고려하세요series RLC circuit, 이는 페이저 도메인으로 표시됩니다.
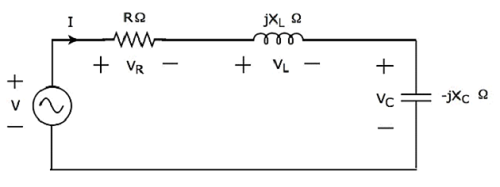
여기서 저항, 인덕터 및 커패시터와 같은 수동 소자는 직렬로 연결됩니다. 이 전체 조합은series 입력 정현파 전압 소스로.
대다 KVL 루프 주위.
$$ V-V_R-V_L-V_C = 0 $$
$$ \ 오른쪽 화살표 V-IR-I (j X_L)-I (-j X_C) = 0 $$
$$ \ 오른쪽 화살표 V = IR + I (j X_L) + I (-j X_C) $$
$ \ 오른쪽 화살표 V = I [R + j (X_L-X_C)] $Equation 1
위의 방정식은 다음과 같습니다. V = IZ.
따라서 impedance Z 시리즈 RLC 회로의
$$ Z = R + j (X_L-X_C) $$
공명시 매개 변수 및 전기적 양
이제 직렬 RLC 회로의 공진에서 매개 변수와 전기량의 값을 하나씩 유도 해 보겠습니다.
공진 주파수
공진이 발생하는 주파수를 resonant frequency fr. 직렬 RLC 회로 공진은 임피던스 Z 의 허수 항이 0 일 때 발생합니다. 즉, $ X_L-X_C $의 값은 0과 같아야합니다.
$$ \ 오른쪽 화살표 X_L = X_C $$
위 방정식에서 $ X_L = 2 \ pi f L $ 및 $ X_C = \ frac {1} {2 \ pi f C} $를 대입합니다.
$$ 2 \ pi f L = \ frac {1} {2 \ pi f C} $$
$$ \ 오른쪽 화살표 f ^ 2 = \ frac {1} {(2 \ pi) ^ 2 LC} $$
$$ \ 오른쪽 화살표 f = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
따라서 resonant frequency fr 시리즈 RLC 회로의
$$ f_r = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
어디, L 인덕터의 인덕턴스이고 C 커패시터의 커패시턴스입니다.
그만큼 resonant frequency fr 직렬 RLC 회로의 수는 인덕턴스에만 의존 L 및 커패시턴스 C. 하지만 저항과는 무관하다R.
임피던스
우리는 impedance Z 시리즈 RLC 회로의
$$ Z = R + j (X_L-X_C) $$
위의 방정식에서 $ X_L = X_C $를 대체하십시오.
$$ Z = R + j (X_C-X_C) $$
$$ \ 오른쪽 화살표 Z = R + j (0) $$
$$ \ 오른쪽 화살표 Z = R $$
공명에서 impedance Z 직렬 RLC 회로의 저항 값과 동일 R즉, Z = R.
회로를 통해 흐르는 전류
방정식 1에서 $ X_L-X_C = 0 $를 대체합니다.
$$ V = I [R + j (0)] $$
$$ \ 오른쪽 화살표 V = IR $$
$$ \ 오른쪽 화살표 I = \ frac {V} {R} $$
따라서, current 공진에서 직렬 RLC 회로를 통해 흐르는 것은 $ \ mathbf {\ mathit {I = \ frac {V} {R}}} $입니다.
공진시 직렬 RLC 회로의 임피던스는 최소값에 도달합니다. 따라서maximum current 공진에서이 회로를 통해 흐릅니다.
저항기 전압
저항의 전압은
$$ V_R = IR $$
가치를 대체하십시오 I 위의 방정식에서.
$$ V_R = \ l 그룹 \ frac {V} {R} \ r 그룹 R $$
$$ \ 오른쪽 화살표 V_R = V $$
따라서 voltage across resistor 공명에서 VR = V.
인덕터 양단 전압
인덕터 양단의 전압은
$$ V_L = I (jX_L) $$
가치를 대체하십시오 I 위의 방정식에서.
$$ V_L = \ l 그룹 \ frac {V} {R} \ r 그룹 (jX_L) $$
$$ \ 오른쪽 화살표 V_L = j \ l 그룹 \ frac {X_L} {R} \ r 그룹 V $$
$$ \ 오른쪽 화살표 V_L = j QV $$
따라서 voltage across inductor 공진에서 $ V_L = j QV $입니다.
그래서 magnitude 공진시 인덕터 양단의 전압은
$$ | V_L | = QV $$
어디 Q 이다 Quality factor 그 값은 $ \ frac {X_L} {R} $와 같습니다.
커패시터 양단 전압
커패시터 양단의 전압은
$$ V_C = I (-j X_C) $$
위의 방정식에서 I 의 값을 대체하십시오 .
$$ V_C = \ l 그룹 \ frac {V} {R} \ r 그룹 (-j X_C) $$
$$ \ 오른쪽 화살표 V_C = -j \ lgroup \ frac {X_C} {R} \ rgroup V $$
$$ \ 오른쪽 화살표 V_C = -jQV $$
따라서 voltage across capacitor 공명에서 $ \ mathbf {\ mathit {V_C = -jQV}} $입니다.
그래서 magnitude 공진시 커패시터 양단의 전압은
$$ | V_C | = QV $$
어디 Q 이다 Quality factor 그 값은 $ \ frac {X_ {C}} {R} $와 같습니다.
Note − 직렬 공진 RLC 회로는 voltage magnification인덕터와 커패시터 양단의 전압 크기 는 입력 정현파 전압 V의 Q 배와 같기 때문 입니다.