네트워크 이론-별에서 델타로 변환
이전 장에서 델타 네트워크를 동등한 스타 네트워크로 변환하는 방법에 대해 논의했습니다. 이제 스타 네트워크를 동등한 델타 네트워크로 변환하는 방법에 대해 논의하겠습니다. 이 변환을Star to Delta Conversion.
이전 장에서 우리는 resistances of star network 델타 네트워크에서
$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ Equation 3
스타 네트워크 저항 측면에서 델타 네트워크 저항
스타 네트워크의 저항 측면에서 델타 네트워크의 저항을 얻기 위해 위의 방정식을 조작 해 보겠습니다.
Multiply 두 방정식의 각 세트 add.
$$ R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 ^ 2 R_3 + R_2 R_3 ^ 2 R_1 + R_3 R_1 ^ 2 R_2} {(R_1 + R_2 + R_3) ^ 2} $$
$$ \ 오른쪽 화살표 R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3 (R_1 + R_2 + R_3)} {(R_1 + R_2 + R_3) ^ 2} $$
$ \ 오른쪽 화살표 R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3} {R_1 + R_2 + R_3} $ Equation 4
방정식 4를 방정식 2로 나누면
$$ \ frac {R_A R_B + R_B R_C + R_C R_A} {R_B} = R_1 $$
$$ \ 오른쪽 화살표 R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
방정식 4를 방정식 3으로 나누면
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
방정식 4를 방정식 1로 나누면
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
위의 관계를 사용하여 스타 네트워크의 저항에서 델타 네트워크의 저항을 찾을 수 있습니다. 이런 식으로 우리는star network into delta network.
예
계산하자 resistances of delta network, 다음 그림과 같이 스타 네트워크와 동일합니다.
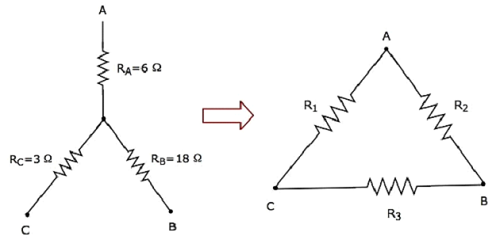
주어진 resistances of star network같은 R = 6 Ω, R B = 18 Ω 및 R C = 3 Ω .
우리는 다음과 같은 관계를 알고 있습니다. resistances of delta network 스타 네트워크의 저항 측면에서.
$$ R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
대체 값 R , R B 및 R C를 상기 수학 식이다.
$$ R_1 = 3 + 6 + \ frac {3 \ times 6} {18} = 9 + 1 = 10 \ Omega $$
$$ R_2 = 6 + 18 + \ frac {6 \ times 18} {3} = 24 + 36 = 60 \ 오메가 $$
$$ R_3 = 18 + 3 + \ frac {18 \ times 3} {6} = 21 + 9 = 30 \ 오메가 $$
그래서 우리는 델타 네트워크의 저항을 다음과 같이 얻었습니다. R1 = 10 Ω, R2 = 60 Ω 과 R3 = 30 Ω, 이는 주어진 스타 네트워크의 저항과 동일합니다.