Optymalizacja wypukła - Minima i Maxima
Lokalne Minima lub Minimalizuj
$ \ bar {x} \ in \: S $ jest lokalnym minimem funkcji $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ gdzie $ N_ \ varepsilon \ left (\ bar {x} \ right) $ oznacza sąsiedztwo $ \ bar {x} $, czyli $ N_ \ varepsilon \ left (\ bar {x} \ right) $ oznacza $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $
Local Maxima lub Maximizer
Mówi się, że $ \ bar {x} \ in \: S $ jest lokalnym maksimem funkcji $ f $ if $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ gdzie $ N_ \ varepsilon \ left (\ bar {x} \ right) $ oznacza sąsiedztwo $ \ bar {x} $, czyli $ N_ \ varepsilon \ left (\ bar {x} \ right) $ oznacza $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $
Globalne minima
Mówi się, że $ \ bar {x} \ in \: S $ jest globalnym minimem funkcji $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in S $
Globalne maksima
$ \ bar {x} \ in \: S $ jest określane jako globalne maksima funkcji $ f $ if $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in S $
Przykłady
Step 1- znajdź lokalne minima i maksima $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ right | $
Solution -

Z wykresu powyższej funkcji jasno wynika, że lokalne minima występują przy $ x = \ pm 2 $, a lokalne maksima przy $ x = 0 $
Step 2- znajdź globalne minima funkcji $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ right | $
Solution -
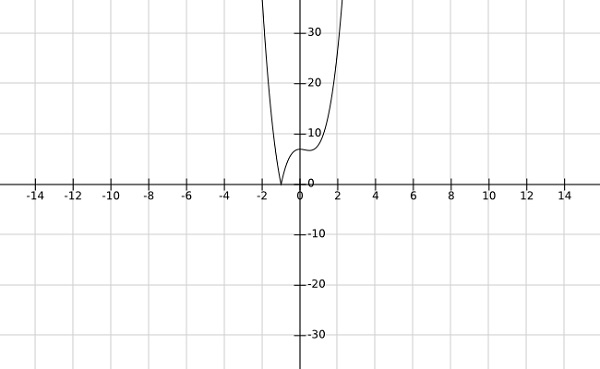
Z wykresu powyższej funkcji jasno wynika, że minima globalne występują przy $ x = -1 $.