Optymalizacja wypukła - krótki przewodnik

Ten kurs jest przydatny dla studentów, którzy chcą rozwiązać nieliniowe problemy optymalizacji, które pojawiają się w różnych zastosowaniach inżynierskich i naukowych. Kurs rozpoczyna się od podstawowej teorii programowania liniowego i wprowadza pojęcia zbiorów wypukłych i funkcji oraz powiązaną terminologię w celu wyjaśnienia różnych twierdzeń wymaganych do rozwiązania problemów programowania nieliniowego. Na tym kursie zostaną przedstawione różne algorytmy używane do rozwiązywania takich problemów. Tego typu problemy pojawiają się w różnych zastosowaniach, w tym w uczeniu maszynowym, problemach optymalizacji w elektrotechnice, itp. Wymaga to od uczniów wcześniejszej znajomości pojęć matematycznych i rachunku różniczkowego w szkole średniej.

Na tym kursie studenci nauczą się rozwiązywać problemy optymalizacyjne, takie jak $min f\left ( x \right )$ podlega pewnym ograniczeniom.

Te problemy można łatwo rozwiązać, jeśli funkcja $f\left ( x \right )$jest funkcją liniową, a więzy są liniowe. Nazywa się to wtedy problemem programowania liniowego (LPP). Ale jeśli ograniczenia są nieliniowe, trudno jest rozwiązać powyższy problem. O ile nie możemy wykreślić funkcji na wykresie, wtedy próba analizy optymalizacji może być jednokierunkowa, ale nie możemy wykreślić funkcji, jeśli wykracza poza trzy wymiary. Stąd pojawiają się techniki programowania nieliniowego lub programowania wypukłego do rozwiązywania takich problemów. W tym samouczku skupimy się na nauce takich technik, a na końcu kilku algorytmów do rozwiązywania takich problemów. najpierw przedstawimy pojęcie zbiorów wypukłych, które jest podstawą wypukłych problemów programistycznych. Następnie, wraz z wprowadzeniem funkcji wypukłych, przedstawimy kilka ważnych twierdzeń służących do rozwiązania tych problemów i niektóre algorytmy oparte na tych twierdzeniach.

Terminologie

• Przestrzeń $\mathbb{R}^n$ - Jest to n-wymiarowy wektor z liczbami rzeczywistymi, zdefiniowanymi następująco - $\mathbb{R}^n=\left \{ \left ( x_1,x_2,...,x_n \right )^{\tau }:x_1,x_2,....,x_n \in \mathbb{R} \right \}$

• Przestrzeń $\mathbb{R}^{mXn}$ - Jest to zbiór wszystkich rzeczywistych macierzy porządku $mXn$.

Metodologia

Programowanie liniowe, zwane także optymalizacją liniową, jest techniką używaną do rozwiązywania problemów matematycznych, w których zależności mają charakter liniowy. podstawową naturą programowania liniowego jest maksymalizacja lub minimalizacjaobjective function z zastrzeżeniem niektórych constraints. Funkcja celu jest funkcją liniową uzyskaną z matematycznego modelu problemu. Więzy to warunki, które są nałożone na model i są również liniowe.

• Na podstawie zadanego pytania znajdź funkcję celu.
• znaleźć ograniczenia.
• Narysuj ograniczenia na wykresie.
• znajdź wykonalny region, który jest utworzony przez przecięcie wszystkich ograniczeń.
• znajdź wierzchołki wykonalnego regionu.
• znajdź wartość funkcji celu w tych wierzchołkach.
• Wierzchołek, który maksymalizuje lub minimalizuje funkcję celu (zgodnie z pytaniem) jest odpowiedzią.

Przykłady

Step 1 - Maksymalizuj $5x+3y$ z zastrzeżeniem

$x+y\leq 2$,

$3x+y\leq 3$,

$x\geq 0 \:and \:y\geq 0$

Solution -

Pierwszym krokiem jest znalezienie odpowiedniego regionu na wykresie.

Wyraźnie z wykresu wynika, że ​​wierzchołki możliwego obszaru są

$\left ( 0, 0 \right )\left ( 0, 2 \right )\left ( 1, 0 \right )\left ( \frac{1}{2}, \frac{3}{2} \right )$

Pozwolić $f\left ( x, y \right )=5x+3y$

Umieszczając te wartości w funkcji celu, otrzymujemy -

$f\left ( 0, 0 \right )$= 0

$f\left ( 0, 2 \right )$= 6

$f\left ( 1, 0 \right )$= 5

$f\left ( \frac{1}{2}, \frac{3}{2} \right )$= 7

Dlatego funkcja maksymalizuje na $\left ( \frac{1}{2}, \frac{3}{2} \right )$

Step 2- Firma zegarmistrzowska produkuje zegarek cyfrowy i mechaniczny. Prognozy długoterminowe wskazują na spodziewane zapotrzebowanie na co najmniej 100 zegarków cyfrowych i 80 zegarków mechanicznych każdego dnia. Ze względu na ograniczenia zdolności produkcyjnej dziennie można wyprodukować nie więcej niż 200 zegarków cyfrowych i 170 mechanicznych. Aby spełnić warunki umowy wysyłkowej, każdego dnia wysyłanych jest co najmniej 200 zegarków.

Jeśli każdy sprzedany zegarek cyfrowy daje wynik $\$2$ loss, but each mechanical watch produces a $\$5$ zysk, ile każdego rodzaju należy zarabiać dziennie, aby zmaksymalizować zysk netto?

Solution -

Pozwolić $x$ być liczbą wyprodukowanych zegarków cyfrowych

$y$ być liczbą wyprodukowanych zegarków mechanicznych

Zgodnie z pytaniem, co najmniej 100 zegarków cyfrowych ma być wykonywanych dziennie i można wykonać maksymalnie 200 zegarków cyfrowych.

$\Rightarrow 100 \leq \:x\leq 200$

Podobnie, co najmniej 80 zegarków mechanicznych ma być wytwarzanych dziennie, a maksymalnie 170 zegarków mechanicznych.

$\Rightarrow 80 \leq \:y\leq 170$

Ponieważ każdego dnia ma być produkowanych co najmniej 200 zegarków.

$\Rightarrow x +y\leq 200$

Ponieważ każdy sprzedany zegarek cyfrowy daje wynik $\$2$ loss, but each mechanical watch produces a $\$5$ zysk,

Całkowity zysk można obliczyć jako

$Profit =-2x + 5y$

I musimy maksymalizować zysk, dlatego pytanie można sformułować jako -

Wyolbrzymiać $-2x + 5y$ z zastrzeżeniem

$100 \:\leq x\:\leq 200$

$80 \:\leq y\:\leq 170$

$x+y\:\leq 200$

Przedstawiając powyższe równania na wykresie, otrzymujemy:

Wierzchołki obszaru wykonalnego to

$\left ( 100, 170\right )\left ( 200, 170\right )\left ( 200, 180\right )\left ( 120, 80\right ) and \left ( 100, 100\right )$

Maksymalną wartość funkcji celu uzyskuje się przy $\left ( 100, 170\right )$ Dlatego, aby zmaksymalizować zyski netto, należy wyprodukować 100 sztuk zegarków cyfrowych i 170 sztuk zegarków mechanicznych.

Norma to funkcja, która nadaje wektorowi lub zmiennej ściśle dodatnią wartość.

Norma jest funkcją $f:\mathbb{R}^n\rightarrow \mathbb{R}$

Podstawowe cechy normy to:

Pozwolić $X$ być takim wektorem $X\in \mathbb{R}^n$

• $\left \| x \right \|\geq 0$

• $\left \| x \right \|= 0 \Leftrightarrow x= 0\forall x \in X$

• $\left \|\alpha x \right \|=\left | \alpha \right |\left \| x \right \|\forall \:x \in X and \:\alpha \:is \:a \:scalar$

• $\left \| x+y \right \|\leq \left \| x \right \|+\left \| y \right \| \forall x,y \in X$

• $\left \| x-y \right \|\geq \left \| \left \| x \right \|-\left \| y \right \| \right \|$

Z definicji norma jest obliczana w następujący sposób -

• $\left \| x \right \|_1=\displaystyle\sum\limits_{i=1}^n\left | x_i \right |$

• $\left \| x \right \|_2=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^2 \right )^{\frac{1}{2}}$

• $\left \| x \right \|_p=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^p \right )^{\frac{1}{p}},1 \leq p \leq \infty$

Norma jest funkcją ciągłą.

Dowód

Z definicji, jeśli $x_n\rightarrow x$ w $X\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right ) $ następnie $f\left ( x \right )$ jest funkcją stałą.

Pozwolić $f\left ( x \right )=\left \| x \right \|$

W związku z tym, $\left | f\left ( x_n \right )-f\left ( x \right ) \right |=\left | \left \| x_n \right \| -\left \| x \right \|\right |\leq \left | \left | x_n-x \right | \:\right |$

Od $x_n \rightarrow x$ a zatem, $\left \| x_n-x \right \|\rightarrow 0$

W związku z tym $\left | f\left ( x_n \right )-f\left ( x \right ) \right |\leq 0\Rightarrow \left | f\left ( x_n \right )-f\left ( x \right ) \right |=0\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right )$

Stąd norma jest funkcją ciągłą.

Iloczyn wewnętrzny to funkcja, która daje skalar parze wektorów.

Produkt wewnętrzny - $f:\mathbb{R}^n \times \mathbb{R}^n\rightarrow \kappa$ gdzie $\kappa$ jest skalarem.

Podstawowe cechy produktu wewnętrznego są następujące -

Pozwolić $X \in \mathbb{R}^n$

• $\left \langle x,x \right \rangle\geq 0, \forall x \in X$

• $\left \langle x,x \right \rangle=0\Leftrightarrow x=0, \forall x \in X$

• $\left \langle \alpha x,y \right \rangle=\alpha \left \langle x,y \right \rangle,\forall \alpha \in \kappa \: and\: \forall x,y \in X$

• $\left \langle x+y,z \right \rangle =\left \langle x,z \right \rangle +\left \langle y,z \right \rangle, \forall x,y,z \in X$

• $\left \langle \overline{y,x} \right \rangle=\left ( x,y \right ), \forall x, y \in X$

Note -

• Związek między normą a iloczynem wewnętrznym: $\left \| x \right \|=\sqrt{\left ( x,x \right )}$

• $\forall x,y \in \mathbb{R}^n,\left \langle x,y \right \rangle=x_1y_1+x_2y_2+...+x_ny_n$

Przykłady

1. Znajdź iloczyn skalarny $x=\left ( 1,2,1 \right )\: and \: y=\left ( 3,-1,3 \right )$

Rozwiązanie

$\left \langle x,y \right \rangle =x_1y_1+x_2y_2+x_3y_3$

$\left \langle x,y \right \rangle=\left ( 1\times3 \right )+\left ( 2\times-1 \right )+\left ( 1\times3 \right )$

$\left \langle x,y \right \rangle=3+\left ( -2 \right )+3$

$\left \langle x,y \right \rangle=4$

2. Jeśli $x=\left ( 4,9,1 \right ),y=\left ( -3,5,1 \right )$ i $z=\left ( 2,4,1 \right )$, odnaleźć $\left ( x+y,z \right )$

Rozwiązanie

Jak wiemy, $\left \langle x+y,z \right \rangle=\left \langle x,z \right \rangle+\left \langle y,z \right \rangle$

$\left \langle x+y,z \right \rangle=\left ( x_1z_1+x_2z_2+x_3z_3 \right )+\left ( y_1z_1+y_2z_2+y_3z_3 \right )$

$\left \langle x+y,z \right \rangle=\left \{ \left ( 4\times 2 \right )+\left ( 9\times 4 \right )+\left ( 1\times1 \right ) \right \}+$

$\left \{ \left ( -3\times2 \right )+\left ( 5\times4 \right )+\left ( 1\times 1\right ) \right \}$

$\left \langle x+y,z \right \rangle=\left ( 8+36+1 \right )+\left ( -6+20+1 \right )$

$\left \langle x+y,z \right \rangle=45+15$

$\left \langle x+y,z \right \rangle=60$

Lokalne Minima lub Minimalizuj

$\bar{x}\in \:S$ mówi się, że są lokalnymi minimami funkcji $f$ gdyby $f\left ( \bar{x} \right )\leq f\left ( x \right ),\forall x \in N_\varepsilon \left ( \bar{x} \right )$ gdzie $N_\varepsilon \left ( \bar{x} \right )$ oznacza sąsiedztwo $\bar{x}$tj. $N_\varepsilon \left ( \bar{x} \right )$oznacza $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Local Maxima lub Maximizer

$\bar{x}\in \:S$ mówi się, że są to lokalne maksima funkcji $f$ gdyby $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in N_\varepsilon \left ( \bar{x} \right )$ gdzie $N_\varepsilon \left ( \bar{x} \right )$ oznacza sąsiedztwo $\bar{x}$tj. $N_\varepsilon \left ( \bar{x} \right )$oznacza $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Globalne minima

$\bar{x}\in \:S$ mówi się, że są to globalne minima funkcji $f$ gdyby $f\left ( \bar{x} \right )\leq f\left ( x \right ), \forall x \in S$

Globalne maksima

$\bar{x}\in \:S$ mówi się, że są to globalne maksima funkcji $f$ gdyby $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in S$

Przykłady

Step 1 - znajdź lokalne minima i maksima $f\left ( \bar{x} \right )=\left | x^2-4 \right |$

Solution -

Z wykresu powyższej funkcji jasno wynika, że ​​lokalne minima występują przy $x= \pm 2$ i lokalne maksima w $x = 0$

Step 2 - znajdź globalne minima funkcji $f\left (x \right )=\left | 4x^3-3x^2+7 \right |$

Solution -

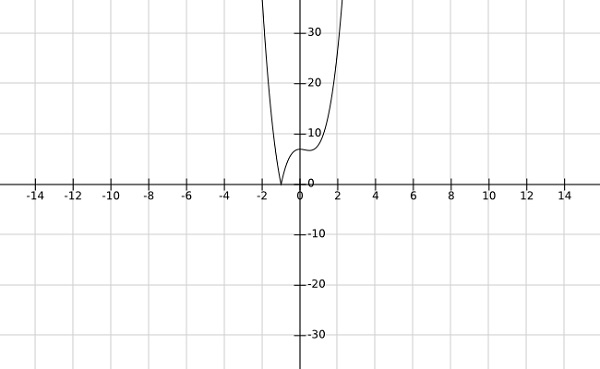
Z wykresu powyższej funkcji jasno wynika, że ​​minima globalne występują przy $x=-1$.

Pozwolić $S\subseteq \mathbb{R}^n$ O zbiorze S mówi się, że jest wypukły, jeśli odcinek linii łączący dowolne dwa punkty zbioru S również należy do S, tj. $x_1,x_2 \in S$, następnie $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S$ gdzie $\lambda \in\left ( 0,1 \right )$.

Note -

• Połączenie dwóch wypukłych zbiorów może być wypukłe lub nie.
• Przecięcie dwóch wypukłych zbiorów jest zawsze wypukłe.

Proof

Pozwolić $S_1$ i $S_2$ być zbiorem dwóch wypukłych.

Pozwolić $S_3=S_1 \cap S_2$

Pozwolić $x_1,x_2 \in S_3$

Od $S_3=S_1 \cap S_2$ a zatem $x_1,x_2 \in S_1$i $x_1,x_2 \in S_2$

Od $S_i$ jest wypukły, $\forall$ $i \in 1,2,$

A zatem $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_i$ gdzie $\lambda \in \left ( 0,1 \right )$

Dlatego $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_1\cap S_2$

$\Rightarrow \lambda x_1+\left ( 1-\lambda \right )x_2 \in S_3$

W związku z tym, $S_3$ jest zbiorem wypukłym.

• Średnia ważona formularza $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$,gdzie $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$ i $\lambda_i\geq 0,\forall i \in \left [ 1,k \right ]$ nazywa się stożkową kombinacją $x_1,x_2,....x_k.$

• Średnia ważona formularza $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$, gdzie $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$ nazywa się połączeniem afinicznym $x_1,x_2,....x_k.$

• Średnia ważona formularza $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ nazywa się liniową kombinacją $x_1,x_2,....x_k.$

Przykłady

Step 1 - Udowodnij, że zestaw $S=\left \{ x \in \mathbb{R}^n:Cx\leq \alpha \right \}$ jest zbiorem wypukłym.

Rozwiązanie

Pozwolić $x_1$ i $x_2 \in S$

$\Rightarrow Cx_1\leq \alpha$ i $\:and \:Cx_2\leq \alpha$

Pokazywać:$\:\:y=\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\in S \:\forall \:\lambda \in\left ( 0,1 \right )$

$Cy=C\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=\lambda Cx_1+\left ( 1-\lambda \right )Cx_2$

$\Rightarrow Cy\leq \lambda \alpha+\left ( 1-\lambda \right )\alpha$

$\Rightarrow Cy\leq \alpha$

$\Rightarrow y\in S$

W związku z tym, $S$ jest zbiorem wypukłym.

Step 2 - Udowodnij, że zestaw $S=\left \{ \left ( x_1,x_2 \right )\in \mathbb{R}^2:x_{1}^{2}\leq 8x_2 \right \}$ jest zbiorem wypukłym.

Rozwiązanie

Pozwolić $x,y \in S$

Pozwolić $x=\left ( x_1,x_2 \right )$ i $y=\left ( y_1,y_2 \right )$

$\Rightarrow x_{1}^{2}\leq 8x_2$ i $y_{1}^{2}\leq 8y_2$

Aby pokazać - $\lambda x+\left ( 1-\lambda \right )y\in S\Rightarrow \lambda \left ( x_1,x_2 \right )+\left (1-\lambda \right )\left ( y_1,y_2 \right ) \in S\Rightarrow \left [ \lambda x_1+\left ( 1- \lambda)y_2] \in S\right ) \right ]$

$Now, \left [\lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}=\lambda ^2x_{1}^{2}+\left ( 1-\lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1-\lambda \right )x_1y_1$

Ale $2x_1y_1\leq x_{1}^{2}+y_{1}^{2}$

W związku z tym,

$\left [ \lambda x_1 +\left ( 1-\lambda \right )y_1\right ]^{2}\leq \lambda ^2x_{1}^{2}+\left ( 1- \lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1- \lambda \right )\left ( x_{1}^{2}+y_{1}^{2} \right )$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq \lambda x_{1}^{2}+\left ( 1- \lambda \right )y_{1}^{2}$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\lambda x_2+8\left ( 1- \lambda \right )y_2$

$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\left [\lambda x_2+\left ( 1- \lambda \right )y_2 \right ]$

$\Rightarrow \lambda x+\left ( 1- \lambda \right )y \in S$

Step 3 - Pokaż ten zestaw $S \in \mathbb{R}^n$ jest wypukła wtedy i tylko wtedy, gdy dla każdej liczby całkowitej k każda wypukła kombinacja dowolnych k punktów $S$ jest w $S$.

Rozwiązanie

Pozwolić $S$być zbiorem wypukłym. następnie, aby pokazać;

$c_1x_1+c_2x_2+.....+c_kx_k \in S, \displaystyle\sum\limits_{1}^k c_i=1,c_i\geq 0, \forall i \in 1,2,....,k$

Dowód przez indukcję

Dla $k=1,x_1 \in S, c_1=1 \Rightarrow c_1x_1 \in S$

Dla $k=2,x_1,x_2 \in S, c_1+c_2=1$ a ponieważ S jest zbiorem wypukłym

$\Rightarrow c_1x_1+c_2x_2 \in S.$

Niech wypukła kombinacja m punktów S jest w S ie,

$c_1x_1+c_2x_2+...+c_mx_m \in S,\displaystyle\sum\limits_{1}^m c_i=1 ,c_i \geq 0, \forall i \in 1,2,...,m$

Teraz pozwól $x_1,x_2....,x_m,x_{m+1} \in S$

Pozwolić $x=\mu_1x_1+\mu_2x_2+...+\mu_mx_m+\mu_{m+1}x_{m+1}$

Pozwolić $x=\left ( \mu_1+\mu_2+...+\mu_m \right )\frac{\mu_1x_1+\mu_2x_2+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}+\mu_{m+1}x_{m+1}$

Pozwolić $y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}$

$\Rightarrow x=\left ( \mu_1+\mu_2+...+\mu_m \right )y+\mu_{m+1}x_{m+1}$

Teraz $y \in S$ ponieważ suma współczynników wynosi 1.

$\Rightarrow x \in S$ ponieważ S jest zbiorem wypukłym i $y,x_{m+1} \in S$

Stąd udowodniono przez indukcję.

Zestaw $A$ mówi się, że jest zbiorem afinicznym, jeśli dla dowolnych dwóch różnych punktów linia przechodząca przez te punkty leży w zbiorze $A$.

Note -

• $S$ jest zbiorem afinicznym wtedy i tylko wtedy, gdy zawiera każdą afiniczną kombinację jego punktów.

• Zbiory puste i pojedyncze są zbiorami afinicznymi i wypukłymi.

  Na przykład rozwiązanie równania liniowego jest zbiorem afinicznym.

Dowód

Niech S będzie rozwiązaniem równania liniowego.

Zgodnie z definicją, $S=\left \{ x \in \mathbb{R}^n:Ax=b \right \}$

Pozwolić $x_1,x_2 \in S\Rightarrow Ax_1=b$ i $Ax_2=b$

Udowodnić : $A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=b, \forall \theta \in\left ( 0,1 \right )$

$A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=\theta Ax_1+\left ( 1-\theta \right )Ax_2=\theta b+\left ( 1-\theta \right )b=b$

Zatem S jest zbiorem afinicznym.

Twierdzenie

Gdyby $C$ jest zbiorem afinicznym i $x_0 \in C$, potem zestaw $V= C-x_0=\left \{ x-x_0:x \in C \right \}$ jest podprzestrzenią C.

Dowód

Pozwolić $x_1,x_2 \in V$

Pokazywać: $\alpha x_1+\beta x_2 \in V$ dla niektórych $\alpha,\beta$

Teraz, $x_1+x_0 \in C$ i $x_2+x_0 \in C$ z definicji V.

Teraz, $\alpha x_1+\beta x_2+x_0=\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0$

Ale $\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0 \in C$ ponieważ C jest zbiorem afinicznym.

W związku z tym, $\alpha x_1+\beta x_2 \in V$

Stąd udowodniono.

Wypukły kadłub zbioru punktów w S jest granicą najmniejszego obszaru wypukłego, który zawiera wszystkie punkty S wewnątrz niego lub na jego granicy.

LUB

Pozwolić $S\subseteq \mathbb{R}^n$ Oznaczono wypukły kadłub litery S $Co\left ( S \right )$ by jest zbiorem wszystkich wypukłych kombinacji S, tj. $x \in Co\left ( S \right )$ wtedy i tylko wtedy gdy $x \in \displaystyle\sum\limits_{i=1}^n \lambda_ix_i$, gdzie $\displaystyle\sum\limits_{1}^n \lambda_i=1$ i $\lambda_i \geq 0 \forall x_i \in S$

Remark - Zbiera kadłub ze zbioru punktów w S na płaszczyźnie definiuje wypukły wielokąt, a punkty S na granicy wielokąta definiują wierzchołki wielokąta.

Theorem $Co\left ( S \right )= \left \{ x:x=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i,x_i \in S, \displaystyle\sum\limits_{i=1}^n \lambda_i=1,\lambda_i \geq 0 \right \}$ Pokaż, że wypukły kadłub jest zbiorem wypukłym.

Dowód

Pozwolić $x_1,x_2 \in Co\left ( S \right )$, następnie $x_1=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i$ i $x_2=\displaystyle\sum\limits_{i=1}^n \lambda_\gamma x_i$ gdzie $\displaystyle\sum\limits_{i=1}^n \lambda_i=1, \lambda_i\geq 0$ i $\displaystyle\sum\limits_{i=1}^n \gamma_i=1,\gamma_i\geq0$

Dla $\theta \in \left ( 0,1 \right ),\theta x_1+\left ( 1-\theta \right )x_2=\theta \displaystyle\sum\limits_{i=1}^n \lambda_ix_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n \gamma_ix_i$

$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n \lambda_i \theta x_i+\displaystyle\sum\limits_{i=1}^n \gamma_i\left ( 1-\theta \right )x_i$

$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]x_i$

Biorąc pod uwagę współczynniki,

$\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]=\theta \displaystyle\sum\limits_{i=1}^n \lambda_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n\gamma_i=\theta +\left ( 1-\theta \right )=1$

W związku z tym, $\theta x_1+\left ( 1-\theta \right )x_2 \in Co\left ( S \right )$

Zatem wypukły kadłub jest zbiorem wypukłym.

Niech S będzie zbiorem arbitralnym $\mathbb{R}^n$.Gdyby $x \in Co\left ( S \right )$, następnie $x \in Co\left ( x_1,x_2,....,x_n,x_{n+1} \right )$.

Dowód

Od $x \in Co\left ( S\right )$, następnie $x$ jest reprezentowany przez wypukłą kombinację skończonej liczby punktów w S, tj.

$x=\displaystyle\sum\limits_{j=1}^k \lambda_jx_j,\displaystyle\sum\limits_{j=1}^k \lambda_j=1, \lambda_j \geq 0$ i $x_j \in S, \forall j \in \left ( 1,k \right )$

Gdyby $k \leq n+1$otrzymany wynik jest oczywiście prawdziwy.

Gdyby $k \geq n+1$, następnie $\left ( x_2-x_1 \right )\left ( x_3-x_1 \right ),....., \left ( x_k-x_1 \right )$ są liniowo zależne.

$\Rightarrow \exists \mu _j \in \mathbb{R}, 2\leq j\leq k$ (nie wszystkie zera) takie, że $\displaystyle\sum\limits_{j=2}^k \mu _j\left ( x_j-x_1 \right )=0$

Definiować $\mu_1=-\displaystyle\sum\limits_{j=2}^k \mu _j$, następnie $\displaystyle\sum\limits_{j=1}^k \mu_j x_j=0, \displaystyle\sum\limits_{j=1}^k \mu_j=0$

gdzie nie wszystko $\mu_j's$są równe zero. Od$\displaystyle\sum\limits_{j=1}^k \mu_j=0$, co najmniej jeden z $\mu_j > 0,1 \leq j \leq k$

Następnie, $x=\displaystyle\sum\limits_{1}^k \lambda_j x_j+0$

$x=\displaystyle\sum\limits_{1}^k \lambda_j x_j- \alpha \displaystyle\sum\limits_{1}^k \mu_j x_j$

$x=\displaystyle\sum\limits_{1}^k\left ( \lambda_j- \alpha\mu_j \right )x_j $

Wybierać $\alpha$ takie że $\alpha=min\left \{ \frac{\lambda_j}{\mu_j}, \mu_j\geq 0 \right \}=\frac{\lambda_j}{\mu _j},$ dla niektórych $i=1,2,...,k$

Gdyby $\mu_j\leq 0, \lambda_j-\alpha \mu_j\geq 0$

Gdyby $\mu_j> 0, then \:\frac{\lambda _j}{\mu_j}\geq \frac{\lambda_i}{\mu _i}=\alpha \Rightarrow \lambda_j-\alpha \mu_j\geq 0, j=1,2,...k$

W szczególności, $\lambda_i-\alpha \mu_i=0$, z definicji $\alpha$

$x=\displaystyle\sum\limits_{j=1}^k \left ( \lambda_j- \alpha\mu_j\right )x_j$,gdzie

$\lambda_j- \alpha\mu_j\geq0$ i $\displaystyle\sum\limits_{j=1}^k\left ( \lambda_j- \alpha\mu_j\right )=1$ i $\lambda_i- \alpha\mu_i=0$

Zatem x można przedstawić jako wypukłą kombinację co najwyżej (k-1) punktów.

Ten proces redukcji można powtarzać, aż x zostanie przedstawione jako wypukła kombinacja (n + 1) elementów.

Niech S będzie niepustym, zamkniętym i ograniczonym zbiorem (zwanym także zbiorem zwartym) w $\mathbb{R}^n$ i pozwól $f:S\rightarrow \mathbb{R} $ być funkcją ciągłą na S, wtedy problem min $\left \{ f\left ( x \right ):x \in S \right \}$ osiąga swoje minimum.

Dowód

Ponieważ S jest niepusty i ograniczony, istnieje dolna granica.

$\alpha =Inf\left \{ f\left ( x \right ):x \in S \right \}$

Teraz pozwól $S_j=\left \{ x \in S:\alpha \leq f\left ( x \right ) \leq \alpha +\delta ^j\right \} \forall j=1,2,...$ i $\delta \in \left ( 0,1 \right )$

Zgodnie z definicją infimium, $S_j$ jest niepusty dla każdego $j$.

Wybierz kilka $x_j \in S_j$ aby uzyskać sekwencję $\left \{ x_j \right \}$ dla $j=1,2,...$

Ponieważ S jest ograniczona, sekwencja jest również ograniczona i istnieje zbieżny podciąg $\left \{ y_j \right \}$, która jest zbieżna z $\hat{x}$. W związku z tym$\hat{x}$ jest punktem granicznym, a S jest zamknięty, dlatego $\hat{x} \in S$. Ponieważ f jest ciągłe,$f\left ( y_i \right )\rightarrow f\left ( \hat{x} \right )$.

Od $\alpha \leq f\left ( y_i \right )\leq \alpha+\delta^k, \alpha=\displaystyle\lim_{k\rightarrow \infty}f\left ( y_i \right )=f\left ( \hat{x} \right )$

A zatem, $\hat{x}$ jest rozwiązaniem minimalizującym.

Uwagi

Twierdzenie Weierstrassa musi spełniać dwa ważne warunki konieczne. Są to następujące -

• Step 1 - Zbiór S powinien być zbiorem ograniczonym.

  Rozważmy funkcję f \ left (x \ right) = x $.

  Jest to zbiór nieograniczony i ma minima w dowolnym punkcie swojej domeny.

  Zatem, aby uzyskać minima, S powinno być ograniczone.

• Step 2 - Zestaw S powinien być zamknięty.

  Rozważmy funkcję $ f \ left (x \ right) = \ frac {1} {x} $ w domenie \ left (0,1 \ right).

  Ta funkcja nie jest zamknięta w danej domenie, nie ma też jej minimów.

  Stąd, aby uzyskać minima, S powinno być zamknięte.

Niech S będzie niepustym, zamkniętym wypukłym zbiorem w $ \ mathbb {R} ^ n$ and let $y \ notin S$, then $\ istnieje$ a point $\ bar {x} \ in S$ with minimum distance from y, i.e.,$\ left \ | y- \ bar {x} \ right \ | \ leq \ left \ | yx \ right \ | \ forall x \ in S. $

Ponadto $ \ bar {x}$ is a minimizing point if and only if $\ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0$ or $\ left (y- \ hat {x}, x- \ hat {x} \ right) \ leq 0 $

Dowód

Istnienie najbliższego punktu

Ponieważ $ S \ ne \ phi, \ istnieje$ a point $\ hat {x} \ in S$ such that the minimum distance of S from y is less than or equal to $\ left \ | y- \ hat {x} \ right \ | $.

Zdefiniuj $ \ hat {S} = S \ cap \ left \ {x: \ left \ | yx \ right \ | \ leq \ left \ | y- \ hat {x} \ right \ | \ right \} $

Od $ \ hat {S}$ is closed and bounded, and since norm is a continuous function, then by Weierstrass theorem, there exists a minimum point $\ hat {x} \ in S$ such that $\ left \ | y- \ hat {x} \ right \ | = Inf \ left \ {\ left \ | yx \ right \ |, x \ in S \ right \} $

Wyjątkowość

Załóżmy, że $ \ bar {x} \ in S$ such that $\ left \ | y- \ hat {x} \ right \ | = \ left \ | y- \ hat {x} \ right \ | = \ alpha $

Ponieważ S jest wypukłe, $ \ frac {\ hat {x} + \ bar {x}} {2} \ w S $

Ale $ \ left \ | y- \ frac {\ hat {x} - \ bar {x}} {2} \ right \ | \ leq \ frac {1} {2} \ left \ | y- \ hat {x} \ right \ | + \ frac {1} {2} \ left \ | y- \ bar {x} \ right \ | = \ alpha $

Nie może to być ścisła nierówność, ponieważ $ \ hat {x} $ jest najbliżej y.

Dlatego $ \ left \ | y- \ hat {x} \ right \ | = \ mu \ left \ | y- \ hat {x} \ right \ |$, for some $\ mu $

Teraz $ \ left \ | \ mu \ right \ | = 1.$ If $\ mu = -1$, then $\ left (y- \ hat {x} \ right) = - \ left (y- \ hat {x} \ right) \ Rightarrow y = \ frac {\ hat {x} + \ bar {x}} {2} \ w S $

Ale $ y \ w S.$. Hence contradiction. Thus $\ mu = 1 \ Rightarrow \ hat {x} = \ bar {x} $

Dlatego punkt minimalizacji jest wyjątkowy.

W drugiej części dowodu załóżmy, że $ \ left (y- \ hat {x} \ right) ^ {\ tau} \ left (x- \ bar {x} \ right) \ leq 0$ for all $x \ w S $

Teraz,

$ \ left \ | yx \ right \ | ^ {2} = \ left \ | y- \ hat {x} + \ hat {x} -x \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ left \ | \ hat {x} -x \ right \ | ^ {2} +2 \ left (\ hat {x} -x \ right) ^ {\ tau} \ left (y- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2}$ because $\ left \ | \ hat {x} -x \ right \ | ^ {2} \ geq 0$ and $\ left (\ hat {x} - x \ right) ^ {T} \ left (y- \ hat {x} \ right) \ geq 0 $

Zatem $ \ hat {x} $ jest punktem minimalizującym.

I odwrotnie, załóżmy, że $ \ hat {x} $ jest minimalnym punktem.

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 \ forall x \ in S $

Ponieważ S jest zbiorem wypukłym.

$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) \ hat {x} = \ hat {x} + \ lambda \ left (x- \ hat {x} \ right) \ in S$ for $x \ w S$ and $\ lambda \ in \ left (0,1 \ right) $

Teraz $ \ left \ | y- \ hat {x} - \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 $

I

$ \ left \ | y- \ hat {x} - \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ {2} -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ {2} \ left \ | x- \ hat {x} \ right \ | -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $

$ \ Rightarrow 2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ 2 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0 $

Stąd udowodnione.

Niech S będzie niepustym, zamkniętym, wypukłym zbiorem w $ \ mathbb {R} ^ n$ and $y \ notin S$. Then, there exists a non zero vector $p$ and scalar $\ beta$ such that $p ^ T y> \ beta$ and $p ^ T x <\ beta$ for each $x \ w S $

Dowód

Ponieważ S nie jest pustym zbiorem zamkniętym wypukłym i $ y \ notin S$ thus by closest point theorem, there exists a unique minimizing point $\ hat {x} \ in S $ takie, że

$ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 \ forall x \ in S $

Niech $ p = \ left (y- \ hat {x} \ right) \ neq 0$ and $\ beta = \ hat {x} ^ T \ left (y- \ hat {x} \ right) = p ^ T \ hat {x} $.

Następnie $ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ T \ left (x- \ hat {x} \ right) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ Tx \ leq \ left (y- \ hat {x} \ right) ^ T \ hat {x} = \ hat {x} ^ T \ left (y- \ hat {x} \ right)$ i,e., $p ^ Tx \ leq \ beta $

Ponadto $ p ^ Ty- \ beta = \ left (y- \ hat {x} \ right) ^ Ty- \ hat {x} ^ T \ left (y- \ hat {x} \ right) $

$ = \ left (y- \ hat {x} \ right) ^ T \ left (yx \ right) = \ left \ | y- \ hat {x} \ right \ | ^ {2}> 0 $

$ \ Rightarrow p ^ Ty> \ beta $

To twierdzenie prowadzi do oddzielenia hiperpłaszczyzn. Hiperpłaszczyzny oparte na powyższym twierdzeniu można zdefiniować następująco:

Niech $ S_1$ and $S_2$ are be non-empty subsets of $\ mathbb {R}$ and $H = \ left \ {X: A ^ TX = b \ right \} $ być hiperpłaszczyzną.

• Mówi się, że hiperpłaszczyzna H oddziela $ S_1$ and $S_2$ if $A ^ TX \ leq b \ forall X \ in S_1$ and $A_TX \ geq b \ forall X \ w S_2 $

• Mówi się, że hiperpłaszczyzna H ściśle oddziela $ S_1$ and $S_2$ if $A ^ TX <b \ forall X \ in S_1$ and $A_TX> b \ forall X \ in S_2 $

• Mówi się, że hiperpłaszczyzna H silnie oddziela $ S_1$ and $S_2$ if $A ^ TX \ leq b \ forall X \ in S_1$ and $A_TX \ geq b + \ varepsilon \ forall X \ in S_2$, where $\ varepsilon $ jest dodatnim skalarem.

Niepusty zbiór C w $ \ mathbb {R} ^ n$ is said to be cone with vertex 0 if $x \ in C \ Rightarrow \ lambda x \ in C \ forall \ lambda \ geq 0 $.

Zbiór C jest wypukłym stożkiem, jeśli jest wypukły, podobnie jak stożek.

Na przykład $ y = \ left | x \ right | $ nie jest wypukłym stożkiem, ponieważ nie jest wypukły.

Ale $ y \ geq \ left | x \ right | $ jest wypukłym stożkiem, ponieważ jest zarówno wypukły jak stożek.

Note - Stożek C jest wypukły wtedy i tylko wtedy, gdy dla dowolnego $ x, y \ w C, x + y \ w C $.

Dowód

Ponieważ C jest stożkiem, dla $ x, y \ w C \ Rightarrow \ lambda x \ w C$ and $\ mu y \ in C \: \ forall \: \ lambda, \ mu \ geq 0 $

C jest wypukłe, jeśli $ \ lambda x + \ left (1- \ lambda \ right) y \ in C \: \ forall \: \ lambda \ in \ left (0, 1 \ right) $

Ponieważ C jest stożkiem, $ \ lambda x \ w C$ and $\ left (1- \ lambda \ right) y \ in C \ Leftrightarrow x, y \ in C $

Zatem C jest wypukłe, jeśli $ x + y \ w C $

Ogólnie rzecz biorąc, jeśli $ x_1, x_2 \ w C$, then, $\ lambda_1x_1 + \ lambda_2x_2 \ in C, \ forall \ lambda_1, \ lambda_2 \ geq 0 $

Przykłady

• Stożkowa kombinacja nieskończonego zbioru wektorów w $ \ mathbb {R} ^ n $ jest stożkiem wypukłym.

• Każdy pusty zestaw jest wypukłym stożkiem.

• Każda funkcja liniowa jest wypukłym stożkiem.

• Ponieważ hiperpłaszczyzna jest liniowa, jest również wypukłym stożkiem.

• Zamknięte półprzestrzenie to również wypukłe stożki.

Note - Przecięcie dwóch wypukłych stożków jest wypukłym stożkiem, ale ich połączenie może, ale nie musi, być wypukłym stożkiem.

Niech S będzie niepustym zbiorem w $ \ mathbb {R} ^ n$ Then, the polar cone of S denoted by $S ^ *$ is given by $S ^ * = \ left \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \: \ forall x \ in S \ right \} $.

Uwaga

• Stożek biegunowy jest zawsze wypukły, nawet jeśli S nie jest wypukły.

• Jeśli S jest pusty, to $ S ^ * = \ mathbb {R} ^ n $.

• Biegunowość można postrzegać jako uogólnienie ortogonalności.

Niech $ C \ subseteq \ mathbb {R} ^ n$ then the orthogonal space of C, denoted by $C ^ \ perp = \ left \ {y \ in \ mathbb {R} ^ n: \ left \ langle x, y \ right \ rangle = 0 \ forall x \ in C \ right \} $.

Lemat

Niech $ S, S_1$ and $S_2$ be non empty sets in $\ mathbb {R} ^ n $ to prawdziwe są następujące stwierdzenia -

• $ S ^ * $ to zamknięty wypukły stożek.

• $ S \ subseteq S ^ {**}$ where $S ^ {**}$ is a polar cone of $S ^ * $.

• $ S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*} $.

Dowód

Step 1 - $ S ^ * = \ left \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \: \ forall \: x \ in S \ right \} $

• Niech $ x_1, x_2 \ in S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0 $ and $x_ {2} ^ {T} x \ leq 0, \ forall x \ in S $

  Dla $ \ lambda \ in \ left (0, 1 \ right), \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] ^ Tx = \ left [\ left (\ lambda x_1 \ right) ) ^ T + \ left \ {\ left (1- \ lambda \ right) x_ {2} \ right \} ^ {T} \ right] x, \ forall x \ in S $

  $ = \ left [\ lambda x_ {1} ^ {T} + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ right] x = \ lambda x_ {1} ^ {T} x + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ leq 0 $

  Zatem $ \ lambda x_1 + \ left (1- \ lambda \ right) x_ {2} \ in S ^ * $

  Dlatego $ S ^ * $ jest zbiorem wypukłym.

• Dla $ \ lambda \ geq 0, p ^ {T} x \ leq 0, \ forall \: x \ in S $

  Dlatego $ \ lambda p ^ T x \ leq 0, $

  $ \ Rightarrow \ left (\ lambda p \ right) ^ T x \ leq 0 $

  $ \ Rightarrow \ lambda p \ in S ^ * $

  Zatem $ S ^ * $ jest stożkiem.

• Aby pokazać $ S ^ *$ is closed, i.e., to show if $p_n \ rightarrow p$ as $n \ rightarrow \ infty$, then $p \ w S ^ * $

  $ \ forall x \ in S, p_ {n} ^ {T} xp ^ T x = \ left (p_n-p \ right) ^ T x $

  Jako $ p_n \ rightarrow p$ as $n \ rightarrow \ infty \ Rightarrow \ left (p_n \ rightarrow p \ right) \ rightarrow 0 $

  Dlatego $ p_ {n} ^ {T} x \ rightarrow p ^ {T} x$. But $p_ {n} ^ {T} x \ leq 0, \: \ forall x \ in S $

  Zatem $ p ^ Tx \ leq 0, \ forall x \ in S $

  $ \ Rightarrow p \ in S ^ * $

  Stąd $ S ^ * $ jest zamknięte.

Step 2 - $ S ^ {**} = \ left \ {q \ in \ mathbb {R} ^ n: q ^ T p \ leq 0, \ forall p \ in S ^ * \ right \} $

Niech $ x \ w S$, then $ \ forall p \ in S ^ *, p ^ T x \ leq 0 \ Rightarrow x ^ Tp \ leq 0 \ Rightarrow x \ in S ^ {**} $

Zatem $ S \ subseteq S ^ {**} $

Step 3 - $ S_2 ^ * = \ left \ {p \ in \ mathbb {R} ^ n: p ^ Tx \ leq 0, \ forall x \ in S_2 \ right \} $

Ponieważ $ S_1 \ subseteq S_2 \ Rightarrow \ forall x \ in S_2 \ Rightarrow \ forall x \ in S_1 $

Dlatego jeśli $ \ hat {p} \ in S_2 ^ *, $then $\ hat {p} ^ Tx \ leq 0, \ forall x \ in S_2 $

$ \ Rightarrow \ hat {p} ^ Tx \ leq 0, \ forall x \ in S_1 $

$ \ Rightarrow \ hat {p} ^ T \ in S_1 ^ * $

$ \ Rightarrow S_2 ^ * \ subseteq S_1 ^ * $

Twierdzenie

Niech C będzie niepustym zamkniętym wypukłym stożkiem, a następnie $ C = C ^ ** $

Dowód

$ C = C ^ {**} $ według poprzedniego lematu.

Aby udowodnić: $ x \ in C ^ {**} \ subseteq C $

Niech $ x \ in C ^ {**}$ and let $x \ notin C $

Zatem według twierdzenia o separacji fundamentalnej istnieje wektor $ p \ neq 0$ and a scalar $\alfa$ such that $p ^ Ty \ leq \ alpha, \ forall y \ in C $

Dlatego $ p ^ Tx> \ alpha $

Ale ponieważ $ \ left (y = 0 \ right) \ in C$ and $p ^ Ty \ leq \ alpha, \ forall y \ in C \ Rightarrow \ alpha \ geq 0$ and $p ^ Tx> 0 $

Jeśli $ p \ notin C ^ *$, then there exists some $\ bar {y} \ w C$ such that $p ^ T \ bar {y}> 0$ and $p ^ T \ left (\ lambda \ bar {y} \ right)$ can be made arbitrarily large by taking $\ lambda $ wystarczająco duże.

Jest to sprzeczne z faktem, że $ p ^ Ty \ leq \ alpha, \ forall y \ in C $

Dlatego $ p \ w C ^ * $

Ponieważ $ x \ in C ^ * = \ left \ {q: q ^ Tp \ leq 0, \ forall p \ in C ^ * \ right \} $

Dlatego $ x ^ Tp \ leq 0 \ Rightarrow p ^ Tx \ leq 0 $

Ale $ p ^ Tx> \ alpha $

Tak jest w przypadku sprzeczności.

Zatem $ x \ w C $

Stąd $ C = C ^ {**} $.

Punkt w postaci $ \ alpha_1x_1 + \ alpha_2x_2 + .... + \ alpha_nx_n$ with $\ alpha_1, \ alpha_2, ..., \ alpha_n \ geq 0$ is called conic combination of $x_1, x_2, ..., x_n. $

• Jeśli $ x_i$ are in convex cone C, then every conic combination of $x_i $ jest również w C.

• Zbiór C jest wypukłym stożkiem, jeśli zawiera wszystkie stożkowe kombinacje jego elementów.

Stożkowy kadłub

Kadłub stożkowy definiuje się jako zbiór wszystkich kombinacji stożkowych danego zbioru S i jest oznaczany przez coni (S).

Zatem $ coni \ lewo (S \ prawo) = \ lewo \ {\ Displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i: x_i \ in S, \ lambda_i \ in \ mathbb {R}, \ lambda_i \ geq 0, i = 1,2, ... \ right \} $

• Stożkowy kadłub to zestaw wypukły.
• Pochodzenie zawsze należy do stożkowego kadłuba.

O zestawie w $ \ mathbb {R} ^ n $ mówi się, że jest wielościenny, jeśli jest przecięciem skończonej liczby zamkniętych półprzestrzeni, tj.

$ S = \ left \ {x \ in \ mathbb {R} ^ n: p_ {i} ^ {T} x \ leq \ alpha_i, i = 1,2, ...., n \ right \} $

Na przykład,

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX = b \ right \} $

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX \ leq b \ right \} $

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX \ geq b \ right \} $

Stożek wielościenny

Zbiór w $ \ mathbb {R} ^ n$ is said to be polyhedral cone if it is the intersection of a finite number of half spaces that contain the origin, i.e., $S = \ left \ {x \ in \ mathbb {R} ^ n: p_ {i} ^ {T} x \ leq 0, i = 1, 2, ... \ right \} $

Polytope

Polytope to zestaw wielościenny, który jest ograniczony.

Uwagi

• Polytope jest wypukłym kadłubem skończonego zbioru punktów.
• Stożek wielościenny jest generowany przez skończony zbiór wektorów.
• Zbiór wielościenny to zbiór zamknięty.
• Zestaw wielościenny to zestaw wypukły.

Niech S będzie zbiorem wypukłym w $ \ mathbb {R} ^ n$. A vector $x \ w S$ is said to be a extreme point of S if $x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2$ with $x_1, x_2 \ w S$ and $\ lambda \ in \ left (0, 1 \ right) \ Rightarrow x = x_1 = x_2 $.

Przykład

Step 1 - $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 1 \ right \ } $

Punkt skrajny, $ E = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} = 1 \ right \} $

Step 2 - $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_1 + x_2 <2, -x_1 + 2x_2 \ leq 2, x_1, x_2 \ geq 0 \ right \ } $

Punkt skrajny, $ E = \ left \ {\ left (0, 0 \ right), \ left (2, 0 \ right), \ left (0, 1 \ right), \ left (\ frac {2} {3 }, \ frac {4} {3} \ right) \ right \} $

Step 3 - S jest polytopem utworzonym przez punkty $ \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2, 4 \ right), \ left (0,2 \ right) \ right \} $

Punkt skrajny, $ E = \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2,4 \ right) \ right \} $

Uwagi

• Dowolny punkt zbioru wypukłego S można przedstawić jako wypukłą kombinację jego skrajnych punktów.

• Jest to prawdziwe tylko dla zbiorów zamkniętych i ograniczonych w $ \ mathbb {R} ^ n $.

• Może to nie być prawdą w przypadku nieograniczonych zestawów.

k skrajnych punktów

Punkt w zbiorze wypukłym nazywa się k ekstremum wtedy i tylko wtedy, gdy jest punktem wewnętrznym k-wymiarowego zbioru wypukłego w S, a nie jest punktem wewnętrznym zbioru (k + 1) - wymiarowego wypukłego w S. Zasadniczo dla zbioru wypukłego S, k skrajne punkty tworzą k-wymiarowe powierzchnie otwarte.

Niech S będzie zbiorem zamkniętym wypukłym w $ \ mathbb {R} ^ n$. A non zero vector $d \ in \ mathbb {R} ^ n$ is called a direction of S if for each $x \ in S, x + \ lambda d \ in S, \ forall \ lambda \ geq 0. $

• Dwa kierunki $ d_1$ and $d_2$ of S are called distinct if $d \ neq \ alpha d_2$ for $ \ alpha> 0 $.

• Kierunek $ d$ of $S$ is said to be extreme direction if it cannot be written as a positive linear combination of two distinct directions, i.e., if $d = \ lambda _1d_1 + \ lambda _2d_2$ for $\ lambda _1, \ lambda _2> 0$, then $d_1 = \ alpha d_2$ for some $\ alpha $.

• Każdy inny kierunek można wyrazić jako dodatnią kombinację skrajnych kierunków.

• Dla wypukłego zestawu $ S$, the direction d such that $x + \ lambda d \ in S$ for some $x \ w S$ and all $Nazywa się \ lambda \ geq0 $ recessive za $ S $.

• Niech E będzie zbiorem punktów, w których dana funkcja $ f: S \ rightarrow$ over a non-empty convex set S in $\ mathbb {R} ^ n$ attains its maximum, then $mi$ is called exposed face of $S $. Kierunki odsłoniętych twarzy nazywane są kierunkami odsłoniętymi.

• Promień, którego kierunek jest skrajnym kierunkiem, nazywany jest promieniem ekstremalnym.

Przykład

Rozważmy funkcję $ f \ left (x \ right) = y = \ left | x \ right |$, where $x \ in \ mathbb {R} ^ n$. Let d be unit vector in $\ mathbb {R} ^ n $

Wówczas d jest kierunkiem funkcji f, ponieważ dla dowolnego $ \ lambda \ geq 0, x + \ lambda d \ in f \ left (x \ right) $.

Niech $ f: S \ rightarrow \ mathbb {R}$, where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ left (x \ right)$ is said to be convex on S if $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ po prawej), \ forall \ lambda \ in \ left (0,1 \ right) $.

Z drugiej strony, niech $ f: S \ rightarrow \ mathbb {R}$, where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ left (x \ right)$ is said to be concave on S if $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ po prawej), \ forall \ lambda \ in \ left (0, 1 \ right) $.

Niech $ f: S \ rightarrow \ mathbb {R}$ where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ left (x \ right)$ is said to be strictly convex on S if $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <\ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) ), \ forall \ lambda \ in \ left (0, 1 \ right) $.

Niech $ f: S \ rightarrow \ mathbb {R}$ where S is non empty convex set in $\ mathbb {R} ^ n$, then $f \ left (x \ right)$ is said to be strictly concave on S if $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)> \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) ), \ forall \ lambda \ in \ left (0, 1 \ right) $.

Przykłady

• Funkcja liniowa jest zarówno wypukła, jak i wklęsła.

• $ f \ left (x \ right) = \ left | x \ right | $ to funkcja wypukła.

• $ f \ left (x \ right) = \ frac {1} {x} $ jest funkcją wypukłą.

Twierdzenie

Niech $ f_1, f_2, ..., f_k: \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ be convex functions. Consider the function $fa \ lewo (x \ w prawo) = \ Displaystyle \ suma \ limity_ {j = 1} ^ k \ alpha_jf_j \ lewo (x \ prawo)$ where $\ alpha_j> 0, j = 1, 2, ... k,$ then $f \ left (x \ right) $ jest funkcją wypukłą.

Dowód

Ponieważ $ f_1, f_2, ... f_k $ są funkcjami wypukłymi

Dlatego $ f_i \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f_i \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_i \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right)$ and $i = 1, 2, ...., k $

Rozważmy funkcję $ f \ left (x \ right) $.

W związku z tym,

$ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) $

$ = \ Displaystyle \ suma \ limity_ {j = 1} ^ k \ alpha_jf_j \ lewo (\ lambda x_1 + 1- \ lambda \ prawo) x_2 \ równoważnik \ Displaystyle \ suma \ limity_ {j = 1} ^ k \ alpha_j \ lambda f_j \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_j \ left (x_2 \ right) $

$ \ Rightarrow f \ lewo (\ lambda x_1 + \ lewo (1- \ lambda \ prawej) x_2 \ prawej) \ równoważnik \ lambda \ lewo (\ Displaystyle \ suma \ limity_ {j = 1} ^ k \ alfa _jf_j \ lewo ( x_1 \ po prawej) \ po prawej) + \ lewo (\ Displaystyle \ suma \ limit_ {j = 1} ^ k \ alpha _jf_j \ lewo (x_2 \ prawo) \ po prawej) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_2 \ right) \ leq \ left (1- \ lambda \ right) f \ lewo (x_2 \ prawo) $

Stąd $ f \ left (x \ right) $ jest funkcją wypukłą.

Twierdzenie

Niech $ f \ left (x \ right)$ be a convex function on a convex set $S \ subset \ mathbb {R} ^ n$ then a local minima of $f \ left (x \ right) $ na S to globalne minimum.

Dowód

Niech $ \ hat {x}$ be a local minima for $f \ left (x \ right)$ and $\ hat {x} $ nie jest globalnym minimem.

dlatego $ \ istnieje \ hat {x} \ w S$ such that $f \ left (\ bar {x} \ right) <f \ left (\ hat {x} \ right) $

Od $ \ hat {x}$ is a local minima, there exists neighbourhood $N_ \ varepsilon \ left (\ hat {x} \ right)$ such that $f \ left (\ hat {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $

Ale $ f \ left (x \ right)$ is a convex function on S, therefore for $\ lambda \ in \ left (0, 1 \ right) $

mamy $ \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ leq \ lambda f \ left (\ hat {x} \ right) + \ left (1- \ lambda \ right) f \ left (\ bar {x} \ right) $

$ \ Rightarrow \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} <\ lambda f \ left (\ hat {x} \ right) + \ left (1- \ lambda \ po prawej) f \ left (\ hat {x} \ right) $

$ \ Rightarrow \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} <f \ left (\ hat {x} \ right), \ forall \ lambda \ in \ left (0 , 1 \ po prawej) $

Ale dla jakiejś $ \ lambda <1 $, ale bliskiej 1, mamy

$ \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S$ and $f \ left (\ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ right) <f \ left (\ bar {x} \ right) $

co jest sprzecznością.

Stąd $ \ bar {x} $ to globalne minimum.

Epigraf

niech S będzie niepustym podzbiorem w $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$ then the epigraph of f denoted by epi(f) or $E_f$ is a subset of $\ mathbb {R} ^ n + 1$ defined by $E_f = \ left \ {\ left (x, \ alpha \ right): x \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R}, f \ left (x \ right) \ leq \ alpha \ right \} $

Hypograph

niech S będzie niepustym podzbiorem w $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$, then the hypograph of f denoted by hyp(f) or $H_f = \ left \ {\ left (x, \ alpha \ right): x \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R}, f \ left (x \ right) \ geq \ alpha \ right \} $

Twierdzenie

Niech S będzie niepustym, wypukłym zbiorem w $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R} ^ n$, then f is convex if and only if its epigraph $E_f $ jest zbiorem wypukłym.

Dowód

Niech f jest funkcją wypukłą.

Aby pokazać $ E_f $ jest zbiorem wypukłym.

Niech $ \ left (x_1, \ alpha_1 \ right), \ left (x_2, \ alpha_2 \ right) \ in E_f, \ lambda \ in \ left (0, 1 \ right) $

Aby wyświetlić $ \ lambda \ left (x_1, \ alpha_1 \ right) + \ left (1- \ lambda \ right) \ left (x_2, \ alpha_2 \ right) \ in E_f $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2, \ lambda \ alpha_1 + \ left (1- \ lambda \ right) \ alpha_2 \ right] \ in E_f $

$ f \ left (x_1 \ right) \ leq \ alpha _1, f \ left (x_2 \ right) \ leq \ alpha _2 $

Dlatego $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda \ alpha_1 + \ left (1- \ lambda \ right) \ alpha_2 $

Rozmawiać

Niech $ E_f $ jest zbiorem wypukłym.

Aby pokazać, że f jest wypukłe.

tj. aby pokazać, czy $ x_1, x_2 \ in S, \ lambda \ left (0, 1 \ right) $

$ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

Niech $ x_1, x_2 \ in S, \ lambda \ in \ left (0, 1 \ right), f \ left (x_1 \ right), f \ left (x_2 \ right) \ in \ mathbb {R} $

Od $ E_f$ is a convex set, $\ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2, \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) \ right) f \ left (x_2 \ right) \ w E_f $

Dlatego $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

Niech S będzie niepustym, wypukłym zbiorem w $ \ mathbb {R} ^ n$ and $f: S \ rightarrow \ mathbb {R} ^ n$. Then f is convex if and only if for each integer $k> 0 $

$ x_1, x_2, ... x_k \ w S, \ Displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1, \ lambda_i \ geq 0, \ forall i = 1,2, s, k$, we have $fa \ lewo (\ Displaystyle \ suma \ limity_ {i = 1} ^ k \ lambda_ix_i \ prawej) \ równoważnik \ Displaystyle \ suma \ limity_ {i = 1} ^ k \ lambda _if \ lewo (x \ w prawo) $

Dowód

Poprzez indukcję k.

$ k = 1: x_1 \ in S$ Therefore $f \ left (\ lambda_1 x_1 \ right) \ leq \ lambda_i f \ left (x_1 \ right)$ because $\ lambda_i = 1 $.

$ k = 2: \ lambda_1 + \ lambda_2 = 1$ and $x_1, x_2 \ w S $

Dlatego $ \ lambda_1x_1 + \ lambda_2x_2 \ w S $

Stąd z definicji $ f \ left (\ lambda_1 x_1 + \ lambda_2 x_2 \ right) \ leq \ lambda _1f \ left (x_1 \ right) + \ lambda _2f \ left (x_2 \ right) $

Niech stwierdzenie jest prawdziwe dla $ n <k $

W związku z tym,

$ f \ left (\ lambda_1 x_1 + \ lambda_2 x_2 + .... + \ lambda_k x_k \ right) \ leq \ lambda_1 f \ left (x_1 \ right) + \ lambda_2 f \ left (x_2 \ right) + ... + \ lambda_k f \ left (x_k \ right) $

$ k = n + 1:$ Let $x_1, x_2, .... x_n, x_ {n + 1} \ in S$ and $\ Displaystyle \ sum \ limity_ {i = 1} ^ {n + 1} = 1 $

Dlatego $ \ mu_1x_1 + \ mu_2x_2 + ....... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ in S $

zatem $ f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) $

$ = f \ left (\ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ right) \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + \ mu_3} + \ mu_ {n + 1} x_ {n + 1} \ right) $

$ = f \ left (\ mu_y + \ mu_ {n + 1} x_ {n + 1} \ right)$ where $\ mu = \ mu_1 + \ mu_2 + ... + \ mu_n $ i

$ y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n}$ and also $\ mu_1 + \ mu_ {n + 1} = 1, y \ w S $

$ \ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ mu f \ left (y \ right) + \ mu_ {n +1} f \ left (x_ {n + 1} \ right) $

$ \ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq $

$ \ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ right) f \ left (\ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} \ right) + \ mu_ {n + 1} f \ left (x_ {n + 1} \ right) $

$ \ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ po prawej) $

$ \ left [\ frac {\ mu_1} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ left (x_1 \ right) + ... + \ frac {\ mu_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ left (x_n \ right) \ right] + \ mu_ {n + 1} f \ left (x_ {n + 1} \ right) $

$ \ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ mu_1f \ left (x_1 \ right) + \ mu_2f \ left ( x_2 \ right) + .... $

Stąd udowodnione.

Niech S będzie niepustym zbiorem otwartym w $ \ mathbb {R} ^ n$,then $f: S \ rightarrow \ mathbb {R}$ is said to be differentiable at $\ hat {x} \ in S$ if there exist a vector $\ bigtriangledown f \ left (\ hat {x} \ right)$ called gradient vector and a function $\ alpha: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $ takie, że

$ f \ left (x \ right) = f \ left (\ hat {x} \ right) + \ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (x- \ hat {x} \ po prawej) + \ lewo \ | x = \ kapelusz {x} \ right \ | \ alpha \ left (\ hat {x}, x- \ hat {x} \ right), \ forall x \ in S $ gdzie

$ \ alpha \ left (\ hat {x}, x- \ hat {x} \ right) \ rightarrow 0 \ bigtriangledown f \ left (\ hat {x} \ right) = \ left [\ frac {\ part f} {\ częściowe x_1} \ frac {\ częściowe f} {\ częściowe x_2} ... \ frac {\ częściowe f} {\ częściowe x_n} \ right] _ {x = \ hat {x}} ^ {T} $

Twierdzenie

niech S będzie niepustym, otwartym, wypukłym zestawem w $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$ be differentiable on S. Then, f is convex if and only if for $x_1, x_2 \ in S, \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right) $

Dowód

Niech f będzie funkcją wypukłą. czyli dla $ x_1, x_2 \ in S, \ lambda \ in \ left (0, 1 \ right) $

$ f \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

$ \ Rightarrow f \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] \ leq \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right ) + f \ left (x_2 \ right) $

$ \ Rightarrow \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right) \ geq f \ left (x_2 + \ lambda \ left (x_1-x_2 \ right) \ right) - f \ left (x_2 \ right) $

$ \ Rightarrow \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right) \ geq f \ left (x_2 \ right) + \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ lambda + $

$ \ left \ | \ lambda \ left (x_1-x_2 \ right) \ right \ | \ alpha \ left (x_2, \ lambda \ left (x_1 - x_2 \ right) -f \ left (x_2 \ right) \ right) $

gdzie $ \ alpha \ left (x_2, \ lambda \ left (x_1 - x_2 \ right) \ right) \ rightarrow 0$ as$\ lambda \ rightarrow 0 $

Dzieląc przez $ \ lambda $ z obu stron, otrzymujemy -

$ f \ left (x_1 \ right) -f \ left (x_2 \ right) \ geq \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) $

Rozmawiać

Niech dla $ x_1, x_2 \ in S, \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right) $

Aby pokazać, że f jest wypukłe.

Ponieważ S jest wypukłe, $ x_3 = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S, \ lambda \ in \ left (0, 1 \ right) $

Zatem od $ x_1, x_3 \ in S $

$ f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 -x_3 \ right) $

$ \ Rightarrow f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 - \ lambda x_1- \ left (1- \ lambda \ right) x_2 \ right) $

$ \ Rightarrow f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ left (1- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 - x_2 \ right) $

Ponieważ $ x_2, x_3 \ in S $, a zatem

$ f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2-x_3 \ right) $

$ \ Rightarrow f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2- \ lambda x_1- \ left (1- \ lambda \ right) x_2 \ right) $

$ \ Rightarrow f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ left (- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ po prawej) $

W ten sposób łącząc powyższe równania otrzymujemy -

$ \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_3 \ right) \ right) + \ left (1- \ lambda \ right) \ left (f \ left (x_2 \ right) -f \ left (x_3 \ right) \ right) \ geq 0 $

$ \ Rightarrow f \ left (x_3 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

Twierdzenie

niech S będzie niepustym otwartym wypukłym zbiorem w $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$ be differentiable on S, then f is convex on S if and only if for any $x_1, x_2 \ in S, \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $

Dowód

niech f będzie funkcją wypukłą, a następnie używając poprzedniego twierdzenia -

$ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right) $ i

$ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq f \ left (x_2 \ right) -f \ left (x_1 \ right) $

Dodając powyższe dwa równania, otrzymujemy -

$ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) + \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $

Rozmawiać

Niech dla każdego $ x_1, x_2 \ in S, \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $

Aby pokazać, że f jest wypukłe.

Niech $ x_1, x_2 \ in S$, thus by mean value theorem, $\ frac {f \ left (x_1 \ right) -f \ left (x_2 \ right)} {x_1-x_2} = \ bigtriangledown f \ left (x \ right), x \ in \ left (x_1-x_2 \ right) \ Rightarrow x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $, ponieważ S jest zbiorem wypukłym.

$ \ Rightarrow f \ left (x_1 \ right) - f \ left (x_2 \ right) = \ left (\ bigtriangledown f \ left (x \ right) ^ T \ right) \ left (x_1-x_2 \ right) $

dla $ x, x_1 $, wiemy -

$ \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x-x_1 \ right) \ geq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2- x_1 \ right) \ geq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (1- \ lambda \ right) \ left (x_2-x_1 \ right) ) \ geq 0 $

$ \ Rightarrow \ bigtriangledown f \ left (x \ right) ^ T \ left (x_2-x_1 \ right) \ geq \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) $

Łącząc powyższe równania, otrzymujemy -

$ \ Rightarrow \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq f \ left (x_2 \ right) -f \ left (x_1 \ right) $

Stąd używając ostatniego twierdzenia, f jest funkcją wypukłą.

Funkcja dwukrotnie różniczkowalna

Niech S będzie niepustym podzbiorem $ \ mathbb {R} ^ n$ and let $f: S \ rightarrow \ mathbb {R}$ then f is said to be twice differentiable at $\ bar {x} \ in S$ if there exists a vector $\ bigtriangledown f \ left (\ bar {x} \ right), a \: nXn$ matrix $H \ lewo (x \ prawo)$(called Hessian matrix) and a function $\ alpha: \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ such that $f \ left (x \ right) = f \ left (\ bar {x} + x- \ bar {x} \ right) = f \ left (\ bar {x} \ right) + \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) + \ frac {1} {2} \ left (x- \ bar {x} \ right) H \ left (\ bar {x} \ right) \ left (x- \ bar {x} \ right) $

gdzie $ \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) \ rightarrow Oasx \ rightarrow \ bar {x} $

Twierdzenie

Niech f będzie funkcją podwójnie różniczkowalną. Jeśli $ \ bar {x}$ is a local minima, then $\ bigtriangledown f \ left (\ bar {x} \ right) = 0$ and the Hessian matrix $H \ left (\ bar {x} \ right) $ jest dodatnią półoskończoną.

Dowód

Niech $ d \ in \ mathbb {R} ^ n$. Since f is twice differentiable at $\ bar {x} $.

W związku z tym,

$ f \ left (\ bar {x} + \ lambda d \ right) = f \ left (\ bar {x} \ right) + \ lambda \ bigtriangledown f \ left (\ bar {x} \ right) ^ T d + \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d + \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d + $

$ \ lambda ^ 2 \ left \ | d \ right \ | ^ 2 \ beta \ left (\ bar {x}, \ lambda d \ right) $

Ale $ \ bigtriangledown f \ left (\ bar {x} \ right) = 0$ and $\ beta \ left (\ bar {x}, \ lambda d \ right) \ rightarrow 0$ as $\ lambda \ rightarrow 0 $

$ \ Rightarrow f \ left (\ bar {x} + \ lambda d \ right) -f \ left (\ bar {x} \ right) = \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d $

Od $ \ bar {x}$ is a local minima, there exists a $\ delta> 0$ such that $f \ left (x \ right) \ leq f \ left (\ bar {x} + \ lambda d \ right), \ forall \ lambda \ in \ left (0, \ delta \ right) $

Twierdzenie

Niech $ f: S \ rightarrow \ mathbb {R} ^ n$ where $S \ subset \ mathbb {R} ^ n$ be twice differentiable over S. If $\ bigtriangledown f \ left (x \ right) = 0$ and $H \ left (\ bar {x} \ right)$ is positive semi-definite, for all $x \ w S$, then $\ bar {x} $ to optymalne rozwiązanie globalne.

Dowód

Od $ H \ left (\ bar {x} \ right)$ is positive semi-definite, f is convex function over S. Since f is differentiable and convex at $\ bar {x} $

$ \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) \ leq f \ left (x \ right) -f \ left (\ bar {x} \ right), \ forall x \ in S $

Ponieważ $ \ bigtriangledown f \ left (\ bar {x} \ right) = 0, f \ left (x \ right) \ geq f \ left (\ bar {x} \ right) $

Stąd $ \ bar {x} $ jest optymalną globalną wartością.

Twierdzenie

Załóżmy, że $ \ bar {x} \ in S$ is a local optimal solution to the problem $f: S \ rightarrow \ mathbb {R}$ where S is a non-empty subset of $\ mathbb {R} ^ n$ and S is convex. $min \: f \ left (x \ right)$ where $x \ w S $.

Następnie:

• $ \ bar {x} $ to optymalne rozwiązanie globalne.

• Jeśli albo $ \ bar {x}$ is strictly local minima or f is strictly convex function, then $\ bar {x} $ to unikalne globalne optymalne rozwiązanie, a także silne lokalne minima.

Dowód

Niech $ \ bar {x}$ be another global optimal solution to the problem such that $x \ neq \ bar {x}$ and $f \ left (\ bar {x} \ right) = f \ left (\ hat {x} \ right) $

Ponieważ $ \ hat {x}, \ bar {x} \ w S$ and S is convex, then $\ frac {\ hat {x} + \ bar {x}} {2} \ in S $ if jest ściśle wypukłe.

$ \ Rightarrow f \ left (\ frac {\ hat {x} + \ bar {x}} {2} \ right) <\ frac {1} {2} f \ left (\ bar {x} \ right) + \ frac {1} {2} f \ left (\ hat {x} \ right) = f \ left (\ hat {x} \ right) $

To jest sprzeczność.

Dlatego $ \ hat {x} $ jest unikalnym, optymalnym rozwiązaniem globalnym.

Następstwo

Niech $ f: S \ subset \ mathbb {R} ^ n \ rightarrow \ mathbb {R}$ be a differentiable convex function where $\ phi \ neq S \ subset \ mathbb {R} ^ n$ is a convex set. Consider the problem $min f \ left (x \ right), x \ in S$,then $\ bar {x}$ is an optimal solution if $\ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) \ geq 0, \ forall x \ in S. $

Dowód

Niech $ \ bar {x}$ is an optimal solution, i.e, $f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in S $

$ \ Rightarrow f \ left (x \ right) = f \ left (\ bar {x} \ right) \ geq 0 $

$ f \ left (x \ right) = f \ left (\ bar {x} \ right) + \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ po prawej) + \ lewo \ | x- \ bar {x} \ right \ | \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) $

gdzie $ \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) \ rightarrow 0$ as $x \ rightarrow \ bar {x} $

$ \ Rightarrow f \ left (x \ right) -f \ left (\ bar {x} \ right) = \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x } \ right) \ geq 0 $

Następstwo

Niech f będzie różniczkowalną wypukłą funkcją przy $ \ bar {x}$,then $\ bar {x}$ is global minimum iff $\ bigtriangledown f \ left (\ bar {x} \ right) = 0 $

Przykłady

• $ f \ left (x \ right) = \ left (x ^ 2-1 \ right) ^ {3}, x \ in \ mathbb {R} $.

  $ \ bigtriangledown f \ left (x \ right) = 0 \ Rightarrow x = -1,0,1 $.

  $ \ bigtriangledown ^ 2f \ left (\ pm 1 \ right) = 0, \ bigtriangledown ^ 2 f \ left (0 \ right) = 6> 0 $.

  $ f \ left (\ pm 1 \ right) = 0, f \ left (0 \ right) = - 1 $

  Stąd $ f \ left (x \ right) \ geq -1 = f \ left (0 \ right) \ Rightarrow f \ left (0 \ right) \ leq f \ left (x \ right) \ forall x \ in \ mathbb {R} $

• $ f \ left (x \ right) = x \ log x$ defined on $S = \ left \ {x \ in \ mathbb {R}, x> 0 \ right \} $.

  $ {f} 'x = 1 + \ log x $

  $ {f} '' x = \ frac {1} {x}> 0 $

  Zatem funkcja ta jest ściśle wypukła.

• $ f \ left (x \ right) = e ^ {x}, x \ in \ mathbb {R} $ jest ściśle wypukłe.

Niech $ f: S \ rightarrow \ mathbb {R}$ where $S \ subset \ mathbb {R} ^ n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1, x_2 \ w S$, we have $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ lambda \ in \ left (0, 1 \ right) $

Na przykład $ f \ left (x \ right) = x ^ {3} $

Niech $ f: S \ rightarrow R $ where $S \ subset \ mathbb {R} ^ n$ is a non-empty convex set. The function f is said to be quasiconvex if for each $x_1, x_2 \ w S$, we have $f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq min \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ lambda \ in \ left (0, 1 \ right) $

Uwagi

• Każda funkcja wypukła jest quasiconvex, ale odwrotność nie jest prawdą.
• Funkcja, która jest zarówno kwazikonwypukła, jak i kwazikonowa, nazywa się kwazimonotonami.

Twierdzenie

Niech $ f: S \ rightarrow \ mathbb {R}$ and S is a non empty convex set in $\ mathbb {R} ^ n$. The function f is quasiconvex if and only if $S _ {\ alpha} = \ left (x \ in S: f \ left (x \ right) \ leq \ alpha \ right \}$ is convex for each real number \alpha$

Dowód

Niech f jest quasiconvex na S.

Pozwolić $x_1,x_2 \in S_{\alpha}$ w związku z tym $x_1,x_2 \in S$ i $max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\leq \alpha$

Pozwolić $\lambda \in \left (0, 1 \right )$ i pozwól $x=\lambda x_1+\left ( 1-\lambda \right )x_2\leq max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\Rightarrow x \in S$

A zatem, $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}\leq \alpha$

W związku z tym, $S_{\alpha}$ jest wypukły.

Rozmawiać

Pozwolić $S_{\alpha}$ jest wypukły dla każdego $\alpha$

$x_1,x_2 \in S, \lambda \in \left ( 0,1\right )$

$x=\lambda x_1+\left ( 1-\lambda \right )x_2$

Pozwolić $x=\lambda x_1+\left ( 1-\lambda \right )x_2$

Dla $x_1, x_2 \in S_{\alpha}, \alpha= max \left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}$

$\Rightarrow \lambda x_1+\left (1-\lambda \right )x_2 \in S_{\alpha}$

$\Rightarrow f \left (\lambda x_1+\left (1-\lambda \right )x_2 \right )\leq \alpha$

Stąd udowodniono.

Twierdzenie

Pozwolić $f:S\rightarrow \mathbb{R}$ a S to niepusty wypukły zestaw w $\mathbb{R}^n$. Funkcja f jest quasiconcave wtedy i tylko wtedy, gdy$S_{\alpha} =\left \{ x \in S:f\left ( x \right )\geq \alpha \right \}$ jest wypukły dla każdej liczby rzeczywistej $\alpha$.

Twierdzenie

Pozwolić $f:S\rightarrow \mathbb{R}$ a S to niepusty wypukły zestaw w $\mathbb{R}^n$. Funkcja f jest quasimonotone wtedy i tylko wtedy, gdy$S_{\alpha} =\left \{ x \in S:f\left ( x \right )= \alpha \right \}$ jest wypukły dla każdej liczby rzeczywistej $\alpha$.

Twierdzenie

Niech S będzie niepustym, wypukłym zbiorem $\mathbb{R}^n$ i $f:S \rightarrow \mathbb{R}$ być różniczkowalne na S, to f jest quasiconvex wtedy i tylko wtedy, gdy dla jakiegokolwiek $x_1,x_2 \in S$ i $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, mamy $\bigtriangledown f\left ( x_2 \right )^T\left ( x_2-x_1 \right )\leq 0$

Dowód

Niech f będzie funkcją quasiconvex.

Pozwolić $x_1,x_2 \in S$ takie że $f\left ( x_1 \right ) \leq f\left ( x_2 \right )$

Przez różniczkowalność f w $x_2, \lambda \in \left ( 0, 1 \right )$

$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=f\left ( x_2+\lambda \left (x_1-x_2 \right ) \right )=f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1-x_2 \right ) \right )$

$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )-f\left ( x_2 \right )-f\left ( x_2 \right )=\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$

$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x2, \lambda\left ( x_1-x_2 \right )\right )$

Ale ponieważ f jest quasiconvex, $f \left ( \lambda x_1+ \left ( 1- \lambda \right )x_2 \right )\leq f \left (x_2 \right )$

$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right ) \right )\leq 0$

Ale $\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right )\right )\rightarrow 0$ tak jak $\lambda \rightarrow 0$

W związku z tym, $\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right ) \leq 0$

Rozmawiać

niech $x_1,x_2 \in S$ i $f\left ( x_1 \right )\leq f\left ( x_2 \right )$, $\bigtriangledown f\left ( x_2 \right )^T \left ( x_1,x_2 \right ) \leq 0$

Aby pokazać, że f jest quasiconvex, tj. $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq f\left ( x_2 \right )$

Proof by contradiction

Załóżmy, że istnieje plik $x_3= \lambda x_1+\left ( 1-\lambda \right )x_2$ takie, że $ f \ left (x_2 \ right) <f \ left (x_3 \ right) $ dla niektórych $ \lambda \in \left ( 0, 1 \right )$

Dla $x_2$ i $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_2-x_3 \right ) \leq 0$

$\Rightarrow -\lambda \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\geq 0$

Dla $x_1$ i $x_3,\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_3 \right ) \leq 0$

$\Rightarrow \left ( 1- \lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )\leq 0$

$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\leq 0$

zatem z powyższych równań $\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )=0$

Definiować $U=\left \{ x:f\left ( x \right )\leq f\left ( x_2 \right ),x=\mu x_2+\left ( 1-\mu \right )x_3, \mu \in \left ( 0,1 \right ) \right \}$

W ten sposób możemy znaleźć $x_0 \in U$ takie że $x_0 = \mu_0 x_2= \mu x_2+\left ( 1- \mu \right )x_3$ dla niektórych $\mu _0 \in \left ( 0,1 \right )$ który jest najbliżej $x_3$ i $\hat{x} \in \left ( x_0,x_1 \right )$ takie, że przez twierdzenie o wartości średniej,

$$\frac{f\left ( x_3\right )-f\left ( x_0\right )}{x_3-x_0}= \bigtriangledown f\left ( \hat{x}\right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x_3-x_0 \right )$$

$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\mu_0 \lambda f\left ( \hat{x}\right )^T \left ( x_1-x_2 \right )$$

Od $x_0$ jest połączeniem $x_1$ i $x_2$ i $ f \ left (x_2 \ right) <f \ left (\ hat {x} \ right) $

Powtarzając procedurę uruchamiania, $\bigtriangledown f \left ( \hat{x}\right )^T \left ( x_1-x_2\right )=0$

W ten sposób łącząc powyższe równania otrzymujemy:

$$f\left ( x_3\right )=f\left ( x_0 \right ) \leq f\left ( x_2\right )$$

$$\Rightarrow f\left ( x_3\right )\leq f\left ( x_2\right )$$

Stąd jest to sprzeczność.

Przykłady

Step 1 - $f\left ( x\right )=X^3$

$Let f \left ( x_1\right )\leq f\left ( x_2\right )$

$\Rightarrow x_{1}^{3}\leq x_{2}^{3}\Rightarrow x_1\leq x_2$

$\bigtriangledown f\left ( x_2 \right )\left ( x_1-x_2 \right )=3x_{2}^{2}\left ( x_1-x_2 \right )\leq 0$

A zatem, $f\left ( x\right )$ jest quasiconvex.

Step 2 - $f\left ( x\right )=x_{1}^{3}+x_{2}^{3}$

Pozwolić $\hat{x_1}=\left ( 2, -2\right )$ i $\hat{x_2}=\left ( 1, 0\right )$

zatem $ f \ left (\ hat {x_1} \ right) = 0, f \ left (\ hat {x_2} \ right) = 1 \ Rightarrow f \ left (\ hat {x_1} \ right) \ setminus <f \ left (\ hat {x_2} \ right) $

A zatem, $\bigtriangledown f \left ( \hat{x_2}\right )^T \left ( \hat{x_1}- \hat{x_2}\right )= \left ( 3, 0\right )^T \left ( 1, -2\right )=3 >0$

W związku z tym $f\left ( x\right )$ nie jest quasiconvex.

Pozwolić $f:S\rightarrow \mathbb{R}^n$ a S być niepustym wypukłym ustawieniem $\mathbb{R}^n$ wtedy mówi się, że f jest funkcją ściśle quasicovex, jeśli dla każdego $x_1,x_2 \in S$ z $f\left ( x_1 \right ) \neq f\left ( x_2 \right )$, mamy $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \: \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} $

Uwagi

• Każda funkcja ściśle quasi-wypukła jest ściśle wypukła.
• Funkcja ściśle quasi-wypukła nie oznacza quasi-wypukłości.
• Funkcja ściśle quasiconvex może nie być silnie quasiconvex.
• Funkcja pseudowypukła jest funkcją ściśle quasikonwypukłą.

Twierdzenie

Pozwolić $f:S\rightarrow \mathbb{R}^n$ być ściśle quasiconvex funkcją, a S być niepustym wypukłym zbiorem w $\mathbb{R}^n$Rozważ problem: $min \:f\left ( x \right ), x \in S$. Gdyby$\hat{x}$ jest zatem lokalnie optymalnym rozwiązaniem $\bar{x}$ to globalne rozwiązanie optymalne.

Dowód

Niech istnieje $ \bar{x} \in S$ takie że $f\left ( \bar{x}\right )\leq f \left ( \hat{x}\right )$

Od $\bar{x},\hat{x} \in S$ a S jest zbiorem wypukłym, dlatego

$$\lambda \bar{x}+\left ( 1-\lambda \right )\hat{x}\in S, \forall \lambda \in \left ( 0,1 \right )$$

Od $\hat{x}$ to lokalne minima, $f\left ( \hat{x} \right ) \leq f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right ), \forall \lambda \in \left ( 0,\delta \right )$

Ponieważ f jest ściśle quasiconvex.

$$ f \ left (\ lambda \ bar {x} + \ left (1- \ lambda \ right) \ hat {x} \ right) <max \ left \ {f \ left (\ hat {x} \ right) , f \ left (\ bar {x} \ right) \ right \} = f \ left (\ hat {x} \ right) $$

Stąd jest to sprzeczność.

Funkcja ściśle quasi-jaskiniowa

Pozwolić $f:S\rightarrow \mathbb{R}^n$ a S być niepustym wypukłym ustawieniem $\mathbb{R}^n$, to f jest saud jako funkcja ściśle quasicovex, jeśli dla każdego $x_1,x_2 \in S$ z $f\left (x_1\right )\neq f\left (x_2\right )$, mamy

$$f\left (\lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$$.

Przykłady

• $f\left (x\right )=x^2-2$

  Jest to funkcja ściśle quasiconvex, ponieważ jeśli weźmiemy dowolne dwa punkty $x_1,x_2$ w domenie, która spełnia ograniczenia z definicji $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} $ Ponieważ funkcja maleje na ujemnej osi x i rośnie na dodatniej osi x (ponieważ jest parabolą).

• $f\left (x\right )=-x^2$

  Nie jest to funkcja ściśle quasiconvex, ponieważ jeśli weźmiemy $x_1=1$ i $x_2=-1$ i $\lambda=0.5$, następnie $f\left (x_1\right )=-1=f\left (x_2\right )$ ale $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )=0$Dlatego nie spełnia warunków określonych w definicji. Ale jest to funkcja quasi-jaskiniowa, ponieważ jeśli weźmiemy dowolne dwa punkty w domenie, które spełniają ograniczenia w definicji$f\left ( \lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$. Ponieważ funkcja rośnie na ujemnej osi x, a maleje na dodatniej osi x.

Pozwolić $f:S\rightarrow \mathbb{R}^n$ a S być niepustym wypukłym ustawieniem $\mathbb{R}^n$ to f jest funkcją silnie quasi-wypukłą, jeśli dla jakiejś $x_1,x_2 \in S$ z $\left ( x_1 \right ) \neq \left ( x_2 \right )$, mamy $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \: \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ forall \ lambda \ in \ left (0,1 \ right) $

Twierdzenie

Funkcja quasiconvex $f:S\rightarrow \mathbb{R}^n$ na niepustym zestawie wypukłym S in $\mathbb{R}^n$ jest funkcją silnie quasiconvex, jeśli nie jest stała na odcinku linii łączącym dowolne punkty S.

Dowód

Niech f jest funkcją quasiconvex i nie jest stała na odcinku prostym łączącym dowolne punkty S.

Załóżmy, że f nie jest funkcją silnie quasiconvex.

Istnieje $x_1,x_2 \in S$ z $x_1 \neq x_2$ takie że

$$f\left ( z \right )\geq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}, \forall z= \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \in \left ( 0,1 \right )$$

$\Rightarrow f\left ( x_1 \right )\leq f\left ( z \right )$ i $f\left ( x_2 \right )\leq f\left ( z \right )$

Ponieważ f nie jest stała w $\left [ x_1,z \right ]$ i $\left [z,x_2 \right ] $

Więc istnieje $u \in \left [ x_1,z \right ]$ i $v=\left [ z,x_2 \right ]$

$$\Rightarrow u= \mu_1x_1+\left ( 1-\mu_1\right )z,v=\mu_2z+\left ( 1- \mu_2\right )x_2$$

Ponieważ f jest quasiconvex,

$$\Rightarrow f\left ( u \right )\leq max\left \{ f\left ( x_1 \right ),f \left ( z \right ) \right \}=f\left ( z \right )\:\: and \:\:f \left ( v \right ) \leq max \left \{ f\left ( z \right ),f\left ( x_2 \right ) \right \}$$

$$\Rightarrow f\left ( u \right )\leq f\left ( z \right ) \:\: and \:\: f\left ( v \right )\leq f\left ( z \right )$$

$$\Rightarrow max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$$

Ale z jest dowolnym punktem między u i v, jeśli którykolwiek z nich jest równy, to f jest stała.

W związku z tym, $max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$

co zaprzecza quasi-wypukłości f as $z \in \left [ u,v \right ]$.

Stąd f jest funkcją silnie quasiconvex.

Twierdzenie

Pozwolić $f:S\rightarrow \mathbb{R}^n$ a S być niepustym wypukłym ustawieniem $\mathbb{R}^n$. Gdyby$\hat{x}$ jest zatem lokalnie optymalnym rozwiązaniem $\hat{x}$ to unikalne globalne optymalne rozwiązanie.

Dowód

Ponieważ silna funkcja quasiconvex jest również funkcją ściśle quasiconvex, zatem optymalnym rozwiązaniem lokalnym jest rozwiązanie optymalne globalnie.

Uniqueness - Niech f osiągnie optymalne globalne rozwiązanie w dwóch punktach $u,v \in S$

$$\Rightarrow f\left ( u \right ) \leq f\left ( x \right ).\forall x \in S\:\: and \:\:f\left ( v \right ) \leq f\left ( x \right ).\forall x \in S$$

Jeśli u jest globalnym optymalnym rozwiązaniem, $f\left ( u \right )\leq f\left ( v \right )$ i $f\left ( v \right )\leq f\left ( u\right )\Rightarrow f\left ( u \right )=f\left ( v\right )$

$$ f \ left (\ lambda u + \ left (1- \ lambda \ right) v \ right) <max \ left \ {f \ left (u \ right), f \ left (v \ right) \ right \} = f \ left (u \ right) $$

co jest sprzecznością.

Dlatego istnieje tylko jedno globalne optymalne rozwiązanie.

Uwagi

• Funkcja silnie quasiconvex jest również funkcją ściśle quasiconvex.
• Funkcja ściśle wypukła może, ale nie musi, być silnie quasikonwypukła.
• Różniczkowalny ściśle wypukły jest silnie quasiconwypukły.

Pozwolić $f:S\rightarrow \mathbb{R}$ być funkcją różniczkowalną, a S niepustym zbiorem wypukłym $\mathbb{R}^n$, to mówi się, że f jest pseudowypukłe, jeśli dla każdego $x_1,x_2 \in S$ z $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, mamy $f\left ( x_2 \right )\geq f\left ( x_1 \right )$lub równoważnie, jeśli $f\left ( x_1 \right )>f\left ( x_2 \right )$ następnie $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) <0 $

Funkcja pseudokończy

Pozwolić $f:S\rightarrow \mathbb{R}$ być funkcją różniczkowalną, a S niepustym zbiorem wypukłym $\mathbb{R}^n$, to mówi się, że f jest pseudowypukłe, jeśli dla każdego $x_1, x_2 \in S$ z $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, mamy $f\left ( x_2 \right )\leq f\left ( x_1 \right )$lub równoważnie, jeśli $f\left ( x_1 \right )>f\left ( x_2 \right )$ następnie $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )>0$

Uwagi

• Jeśli funkcja jest zarówno pseudowypukła, jak i pseudo-wypukła, wówczas nazywa się ją pseudoliniową.

• Różniczkowalna funkcja wypukła jest również pseudo wypukła.

• Funkcja pseudowypukła nie może być wypukła. Na przykład,

  $f\left ( x \right )=x+x^3$nie jest wypukła. Gdyby$x_1 \leq x_2,x_{1}^{3} \leq x_{2}^{3}$

  A zatem,$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )=\left ( 1+3x_{1}^{2} \right )\left ( x_2-x_1 \right ) \geq 0$

  I, $f\left ( x_2 \right )-f\left ( x_1 \right )=\left ( x_2-x_1 \right )+\left ( x_{2}^{3} -x_{1}^{3}\right )\geq 0$

  $\Rightarrow f\left ( x_2 \right )\geq f\left ( x_1 \right )$

  Tak więc jest pseudo wypukły.

  Funkcja pseudowypukła jest ściśle quasiconvex. Zatem każde lokalne minima pseudowypukłości są również minimami globalnymi.

Funkcja ściśle pseudo wypukła

Pozwolić $f:S\rightarrow \mathbb{R}$ być funkcją różniczkowalną, a S niepustym zbiorem wypukłym $\mathbb{R}^n$, to mówi się, że f jest pseudowypukłe, jeśli dla każdego $x_1,x_2 \in S$ z $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$, mamy $f\left ( x_2 \right )> f\left ( x_1 \right )$lub równoważnie, jeśli $f\left ( x_1 \right )\geq f\left ( x_2 \right )$ następnie $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) <0 $

Twierdzenie

Niech f będzie funkcją pseudo wypukłą i przypuśćmy $\bigtriangledown f\left ( \hat{x}\right )=0$ dla niektórych $\hat{x} \in S$, następnie $\hat{x}$ jest globalnym optymalnym rozwiązaniem f nad S.

Dowód

Pozwolić $\hat{x}$ być punktem krytycznym f, tj. $\bigtriangledown f\left ( \hat{x}\right )=0$

Ponieważ f jest funkcją pseudo wypukłą, dla $x \in S,$ mamy

$$\bigtriangledown f\left ( \hat{x}\right )\left ( x-\hat{x}\right )=0 \Rightarrow f\left ( \hat{x}\right )\leq f\left ( x\right ), \forall x \in S$$

W związku z tym, $\hat{x}$ to globalne rozwiązanie optymalne.

Uwaga

Jeśli f jest funkcją ściśle pseudowypukłą, $\hat{x}$ to unikalne globalne optymalne rozwiązanie.

Twierdzenie

Jeśli f jest różniczkowalną funkcją pseudowypukłą nad S, to f jest zarówno funkcją ściśle quasiconvex, jak i quasiconvex.

Uwagi

• Suma dwóch funkcji pseudowypukłych zdefiniowanych na zbiorze otwartym S równym $\mathbb{R}^n$ nie może być pozornie wypukłe.

• Pozwolić $f:S\rightarrow \mathbb{R}$ być funkcją quasi-wypukłą, a S niepustym podzbiorem wypukłym $\mathbb{R}^n$ wtedy f jest pseudowypukłe wtedy i tylko wtedy, gdy każdy punkt krytyczny jest globalnym minimum f nad S.

• Niech S będzie niepustym, wypukłym podzbiorem $\mathbb{R}^n$ i $f:S\rightarrow \mathbb{R}$ być taką funkcją $\bigtriangledown f\left ( x\right )\neq 0$ dla każdego $x \in S$ to f jest pseudowypukłe wtedy i tylko wtedy, gdy jest funkcją quasi-wypukłą.

Istnieją cztery typy wypukłych problemów programistycznych -

Step 1 - $min \:f\left ( x \right )$, gdzie $x \in S$ a S być niepustym wypukłym ustawieniem $\mathbb{R}^n$ i $f\left ( x \right )$ jest funkcją wypukłą.

Step 2 - $min \: f\left ( x \right ), x \in \mathbb{R}^n$ z zastrzeżeniem

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ i $g_i\left ( x \right )$ jest funkcją wypukłą.

$g_i\left ( x \right ) \leq 0,m_1+1 \leq m_2$ i $g_i\left ( x \right )$ jest funkcją wklęsłą.

$g_i\left ( x \right ) = 0, m_2+1 \leq m$ i $g_i\left ( x \right )$ jest funkcją liniową.

gdzie $f\left ( x \right )$ jest funkcją wypukłą.

Step 3 - $max \:f\left ( x \right )$ gdzie $x \in S$ a S być niepustym wypukłym ustawieniem $\mathbb{R}^n$ i $f\left ( x \right )$ jest funkcją wklęsłą.

Step 4 - $min \:f\left ( x \right )$, gdzie $x \in \mathbb{R}^n$ z zastrzeżeniem

$g_i\left ( x \right ) \geq 0, 1 \leq m_1$ i $g_i\left ( x \right )$ jest funkcją wypukłą.

$g_i\left ( x \right ) \leq 0, m_1+1 \leq m_2$ i $g_i\left ( x \right )$ jest funkcją wklęsłą.

$g_i\left ( x \right ) = 0,m_2+1 \leq m$ i $g_i\left ( x \right )$ jest funkcją liniową.

gdzie $f\left ( x \right )$ jest funkcją wklęsłą.

Stożek wykonalnego kierunku

Niech S będzie niepustym zbiorem $\mathbb{R}^n$ i pozwól $\hat{x} \in \:Closure\left ( S \right )$, a następnie stożek wykonalnego kierunku S w $\hat{x}$, oznaczony przez D, jest zdefiniowany jako $D=\left \{ d:d\neq 0,\hat{x}+\lambda d \in S, \lambda \in \left ( 0, \delta \right ), \delta > 0 \right \}$

Każdy niezerowy wektor $d \in D$ nazywa się wykonalnym kierunkiem.

Dla danej funkcji $f:\mathbb{R}^n \Rightarrow \mathbb{R}$ stożek poprawy kierunku przy $\hat{x}$ jest oznaczony przez F i jest określony przez

$$F=\left \{ d:f\left ( \hat{x}+\lambda d \right )\leq f\left ( \hat{x} \right ),\forall \lambda \in \left ( 0,\delta \right ), \delta >0 \right \}$$

W każdym kierunku $d \in F$ nazywany jest poprawiającym się kierunkiem lub kierunkiem opadania f w $\hat{x}$

Twierdzenie

Necessary Condition

Rozważ problem $min f\left ( x \right )$ takie że $x \in S$ gdzie S jest niepustym zestawem w $\mathbb{R}^n$. Załóżmy, że f jest różniczkowalne w punkcie$\hat{x} \in S$. Gdyby$\hat{x}$ jest zatem lokalnie optymalnym rozwiązaniem $F_0 \cap D= \phi$ gdzie $ F_0 = \ left \ {d: \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 \ right \} $ i D to stożek o możliwym kierunku.

Sufficient Condition

Gdyby $F_0 \cap D= \phi$ f jest funkcją pseudowypukłą w $\hat{x}$ i istnieje sąsiedztwo $\hat{x},N_\varepsilon \left ( \hat{x} \right ), \varepsilon > 0$ takie że $d=x-\hat{x}\in D$ dla każdego $x \in S \cap N_\varepsilon \left ( \hat{x} \right )$, następnie $\hat{x}$ jest lokalnym optymalnym rozwiązaniem.

Dowód

Necessary Condition

Pozwolić $F_0 \cap D\neq \phi$, tj. istnieje plik $d \in F_0 \cap D$ takie że $d \in F_0$ i $d\in D$

Od $d \in D$dlatego istnieje $\delta_1 >0$ takie że $\hat{x}+\lambda d \in S, \lambda \in \left ( 0,\delta_1 \right ).$

Od $d \in F_0$, więc $ \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 $

Tak więc istnieje $\delta_2>0$ takie, że $ f \ left (\ hat {x} + \ lambda d \ right) <f \ left (\ hat {x} \ right), \ forall \ lambda \ in f \ left (0, \ delta_2 \ right) $

Pozwolić $\delta=min \left \{\delta_1,\delta_2 \right \}$

Następnie $ \ hat {x} + \ lambda d \ in S, f \ left (\ hat {x} + \ lambda d \ right) <f \ left (\ hat {x} \ right), \ forall \ lambda \ w f \ left (0, \ delta \ right) $

Ale $\hat{x}$ jest lokalnym optymalnym rozwiązaniem.

Stąd jest to sprzeczność.

A zatem $F_0\cap D=\phi$

Sufficient Condition

Pozwolić $F_0 \cap D\neq \phi$ i niech f będzie funkcją pseudowypukłą.

Niech istnieje sąsiedztwo $\hat{x}, N_{\varepsilon}\left ( \hat{x} \right )$ takie że $d=x-\hat{x}, \forall x \in S \cap N_\varepsilon\left ( \hat{x} \right )$

Pozwolić $\hat{x}$ is not a local optimal solution.

Thus, there exists $\bar{x} \in S \cap N_\varepsilon \left ( \hat{x} \right )$ such that $f \left ( \bar{x} \right )< f \left ( \hat{x} \right )$

By assumption on $S \cap N_\varepsilon \left ( \hat{x} \right ),d=\left ( \bar{x}-\hat{x} \right )\in D$

By pseudoconvex of f,

$$f\left ( \hat{x} \right )>f\left ( \bar{x} \right )\Rightarrow \bigtriangledown f\left ( \hat{x} \right )^T\left ( \bar{x}-\hat{x} \right )<0$$

$\Rightarrow \bigtriangledown f\left ( \hat{x} \right) ^T d <0$

$\Rightarrow d \in F_0$

hence $F_0\cap D \neq \phi$

which is a contradiction.

Hence, $\hat{x}$ is local optimal solution.

Consider the following problem:$min \:f\left ( x\right )$ where $x \in X$ such that $g_x\left ( x\right ) \leq 0, i=1,2,...,m$

$f:X \rightarrow \mathbb{R},g_i:X \rightarrow \mathbb{R}^n$ and X is an open set in $\mathbb{R}^n$

Let $S=\left \{x:g_i\left ( x\right )\leq 0,\forall i \right \}$

Let $\hat{x} \in X$, then $M=\left \{1,2,...,m \right \}$

Let $I=\left \{i:g_i\left ( \hat{x}\right )=0, i \in M\right \}$ where I is called index set for all active constraints at $\hat{x}$

Let $J=\left \{i:g_i\left ( \hat{x}\right )<0,i \in M\right \}$ where J is called index set for all active constraints at $\hat{x}$.

Let $F_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown f\left ( \hat{x} \right )^T d <0 \right \}$

Let $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gI\left ( \hat{x} \right )^T d <0 \right \}$

or $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gi\left ( \hat{x} \right )^T d <0 ,\forall i \in I \right \}$

Lemma

If $S=\left \{ x \in X:g_i\left ( x\right ) \leq 0, \forall i \in I\right \}$ and X is non-empty open set in $\mathbb{R}^n$. Let $\hat{x}\in S$ and $g_i$ are different at $\hat{x}, i \in I$ and let $g_i$ where $i \in J$ are continuous at $\hat{x}$, then $G_0 \subseteq D$.

Proof

Let $d \in G_0$

Since $\hat{x} \in X$ and X is an open set, thus there exists $\delta_1 >0$ such that $\hat{x}+\lambda d \in X$ for $\lambda \in \left ( 0, \delta_1\right )$

Also since $g_\hat{x}<0$ and $g_i$ are continuous at $\hat{x}, \forall i \in J$, there exists $\delta_2>0$, $g_i\left ( \hat{x}+\lambda d\right )<0, \lambda \in \left ( 0, \delta_2\right )$

Since $d \in G_0$, therefore, $\bigtriangledown g_i\left ( \hat{x}\right )^T d <0, \forall i \in I$ thus there exists $\delta_3 >0, g_i\left ( \hat{x}+\lambda d\right )< g_i\left ( \hat{x}\right )=0$, for $\lambda \in \left ( 0, \delta_3\right ) i \in J$

Let $\delta=min\left \{ \delta_1, \delta_2, \delta_3 \right \}$

therefore, $\hat{x}+\lambda d \in X, g_i\left ( \hat{x}+\lambda d\right )< 0, i \in M$

$\Rightarrow \hat{x}+\lambda d \in S$

$\Rightarrow d \in D$

$\Rightarrow G_0 \subseteq D$

Hence Proved.

Theorem

Necessary Condition

Let $f$ and $g_i, i \in I$, are different at $\hat{x} \in S,$ and $g_j$ are continous at $\hat{x} \in S$. If $\hat{x}$ is local minima of $S$, then $F_0 \cap G_0=\phi$.

Sufficient Condition

If $F_0 \cap G_0= \phi$ and f is a pseudoconvex function at $\left (\hat{x}, g_i 9x \right ), i \in I$ are strictly pseudoconvex functions over some $\varepsilon$ - neighbourhood of $\hat{x}, \hat{x}$ is a local optimal solution.

Uwagi

• Pozwolić $\hat{x}$ być takim punktem wykonalnym $\bigtriangledown f\left(\hat{x} \right)=0$, następnie $F_0 = \phi$. A zatem,$F_0 \cap G_0= \phi$ ale $\hat{x}$ nie jest optymalnym rozwiązaniem

• Ale jeśli $\bigtriangledown g\left(\hat{x} \right)=0$, następnie $G_0=\phi$, więc $F_0 \cap G_0= \phi$

• Rozważ problem: min $f\left(x \right)$ takie że $g\left(x \right)=0$.

  Od $g\left(x \right)=0$, więc $ g_1 \ left (x \ right) = g \ left (x \ right) <0 $ i $g_2\left(x \right)=-g\left(x \right) \leq 0$.

  Pozwolić $\hat{x} \in S$, następnie $g_1\left(\hat{x} \right)=0$ i $g_2\left(\hat{x} \right)=0$.

  Ale $\bigtriangledown g_1\left(\hat{x} \right)= - \bigtriangledown g_2\left(\hat{x}\right)$

  A zatem, $G_0= \phi$ i $F_0 \cap G_0= \phi$.

Niezbędne warunki

Twierdzenie

Rozważ problem - $min f\left ( x \right )$ takie że $x \in X$ gdzie X to zbiór otwarty $\mathbb{R}^n$ i pozwól $g_i \left ( x \right ) \leq 0, \forall i =1,2,....m$.

Pozwolić $f:X \rightarrow \mathbb{R}$ i $g_i:X \rightarrow \mathbb{R}$

Pozwolić $\hat{x}$ być wykonalnym rozwiązaniem i niech f i $g_i, i \in I$ są zróżnicowane w $\hat{x}$ i $g_i, i \in J$ są ciągłe o godz $\hat{x}$.

Gdyby $\hat{x}$ rozwiązuje powyższy problem lokalnie, wtedy istnieje $u_0, u_i \in \mathbb{R}, i \in I$ takie że $u_0 \bigtriangledown f\left ( \hat{x} \right )+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i \left ( \hat{x} \right )$= 0

gdzie $u_0,u_i \geq 0,i \in I$ i $\left ( u_0, u_I \right ) \neq \left ( 0,0 \right )$

Ponadto, jeśli $g_i,i \in J$ są również zróżnicowane w $\hat{x}$, to powyższe warunki można zapisać jako -

$u_0 \bigtriangledown f\left ( \hat{x}\right )+\displaystyle\sum\limits_{i=1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right )=0$

$u_ig_i\left (\hat{x} \right )$= 0

$u_0,u_i \geq 0, \forall i=1,2,....,m$

$\left (u_0,u \right ) \neq \left ( 0,0 \right ), u=\left ( u_1,u_2,s,u_m \right ) \in \mathbb{R}^m$

Uwagi

• $u_i$ nazywane są mnożnikami Lagrange'a.

• Warunek, że $\hat{x}$ być wykonalne dla danego problemu nazywa się pierwotnym warunkiem wykonalnym.

• Wymaganie $u_0 \bigtriangledown f\left (\hat{x} \right )+\displaystyle\sum\limits_{i=1}^m u-i \bigtriangledown g_i\left ( x \right )=0$ nazywany jest podwójnym warunkiem wykonalności.

• Warunek $u_ig_i\left ( \hat{x} \right )=0, i=1, 2, ...m$Nazywa się to uzupełniającym stanem rozluźnienia. Ten warunek wymaga$u_i=0, i \in J$

• Pierwotny warunek wykonalności, podwójny warunek wykonalności i uzupełniająca się niezdolność nazywane są warunkami Fritza-Johna.

Wystarczające warunki

Twierdzenie

Jeśli istnieje $\varepsilon$-w sąsiedztwie $\hat{x}N_\varepsilon \left ( \hat{x} \right ),\varepsilon >0$ takie, że f jest pseudo wypukłe $N_\varepsilon \left ( \hat{x} \right )\cap S$ i $g_i,i \in I$ są ściśle pseudowypukłe $N_\varepsilon \left ( \hat{x}\right )\cap S$, następnie $\hat{x}$jest lokalnie optymalnym rozwiązaniem opisanego powyżej problemu. Jeśli f jest pseudo wypukłe w$\hat{x}$ i jeśli $g_i, i \in I$ są zarówno ściśle pseudowypukłe, jak i quasiconvex $\hat{x},\hat{x}$ jest globalnym optymalnym rozwiązaniem opisanego powyżej problemu.

Przykład

• $min \:f\left ( x_1,x_2 \right )=\left ( x_1-3 \right )^2+\left ( x_2-2 \right )^2$

  takie że $x_{1}^{2}+x_{2}^{2} \leq 5, x_1+2x_2 \leq 4, x_1,x_2 \geq 0$ I $\hat{x}=\left ( 2,1 \right )$

  Pozwolić $g_1\left (x_1,x_2 \right )=x_{1}^{2}+x_{2}^{2} -5,$

  $g_2\left (x_1,x_2 \right )=x_1+2x_2-4,$

  $g_3\left (x_1,x_2 \right )=-x_1$ i $g_4\left ( x_1, x_2 \right )= -x_2$.

  Zatem powyższe ograniczenia można zapisać jako -

  $g_1\left (x_1,x_2 \right )\leq 0,$

  $g_2\left (x_1,x_2 \right )\leq 0,$

  $g_3\left (x_1,x_2 \right )\leq 0$ i

  $g_4\left (x_1,x_2 \right )\leq 0$ A zatem, $I = \left \{1,2 \right \}$ w związku z tym, $u_3=0,u_4=0$

  $\bigtriangledown f \left (\hat{x} \right )=\left (2,-2 \right ),\bigtriangledown g_1\left (\hat{x} \right )=\left (4,2 \right )$ i $\bigtriangledown g_2\left (\hat{x} \right )=\left (1,2 \right )$

  W ten sposób umieszczając te wartości w pierwszym warunku warunków Fritza-Johna, otrzymujemy -

  $u_0=\frac{3}{2} u_2, \:\:u_1= \frac{1}{2}u_2,$ i pozwól $u_2=1$, w związku z tym $u_0= \frac{3}{2},\:\:u_1= \frac{1}{2}$

  Zatem warunki Fritza Johna są spełnione.

• $min f\left (x_1,x_2\right )=-x_1$.

  takie że $x_2-\left (1-x_1\right )^3 \leq 0$,

  $-x_2 \leq 0$ i $\hat{x}=\left (1,0\right )$

  Pozwolić $g_1\left (x_1,x_2 \right )=x_2-\left (1-x_1\right )^3$,

  $g_2\left (x_1,x_2 \right )=-x_2$

  Zatem powyższe ograniczenia można zapisać jako -

  $g_1\left (x_1,x_2 \right )\leq 0,$

  $g_2\left (x_1,x_2 \right )\leq 0,$

  A zatem, $I=\left \{1,2 \right \}$

  $\bigtriangledown f\left (\hat{x} \right )=\left (-1,0\right )$

  $\bigtriangledown g_1 \left (\hat{x} \right )=\left (0,1\right )$ i $g_2 \left (\hat{x} \right )=\left (0, -1 \right )$

  W ten sposób umieszczając te wartości w pierwszym warunku warunków Fritza-Johna, otrzymujemy -

  $u_0=0,\:\: u_1=u_2=a>0$

  Zatem warunki Fritza Johna są spełnione.

Rozważ problem -

$min \:f\left ( x \right )$ takie że $x \in X$, gdzie X to otwarty zbiór w $\mathbb{R}^n$ i $g_i \left ( x \right )\leq 0, i=1, 2,...,m$

Pozwolić $S=\left \{ x \in X:g_i\left ( x \right )\leq 0, \forall i \right \}$

Pozwolić $\hat{x} \in S$ i pozwól $f$ i $g_i,i \in I$ są zróżnicowane w $\hat{x}$ i $g_i, i \in J$ są ciągłe o godz $\hat{x}$. Ponadto,$\bigtriangledown g_i\left ( \hat{x} \right), i \in I$są liniowo niezależne. Gdyby$\hat{x}$ rozwiązuje powyższy problem lokalnie, wtedy istnieje $u_i,i \in I$ takie że

$\bigtriangledown f\left ( x\right)+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$, $\:\:u_i \geq 0, i \in I$

Gdyby $g_i,i \in J$ są również zróżnicowane w $\hat{x}$. następnie$\hat{x}$, następnie

$\bigtriangledown f\left ( \hat{x}\right)+\displaystyle\sum\limits_{i= 1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$

$u_ig_i\left ( \hat{x} \right)=0, \forall i=1,2,...,m$

$u_i \geq 0 \forall i=1,2,...,m$

Przykład

Rozważ następujący problem -

$min \:f\left ( x_1,x_2 \right )=\left ( x_1-3\right )^2+\left ( x_2-2\right )^2$

takie że $x_{1}^{2}+x_{2}^{2}\leq 5$,

$x_1,2x_2 \geq 0$ i $\hat{x}=\left ( 2,1 \right )$

Pozwolić $g_1\left ( x_1, x_2 \right)=x_{1}^{2}+x_{2}^{2}-5$,

$g_2\left ( x_1, x_2 \right)=x_{1}+2x_2-4$

$g_3\left ( x_1, x_2 \right)=-x_{1}$ i $g_4\left ( x_1,x_2 \right )=-x_2$

Zatem powyższe ograniczenia można zapisać jako -

$g_1 \left ( x_1,x_2 \right)\leq 0, g_2 \left ( x_1,x_2 \right) \leq 0$

$g_3 \left ( x_1,x_2 \right)\leq 0,$ i $g_4 \left ( x_1,x_2 \right) \leq 0$ A zatem, $I=\left \{ 1,2 \right \}$ w związku z tym, $ u_3=0,\:\: u_4=0$

$\bigtriangledown f \left ( \hat{x} \right)=\left ( 2,-2 \right), \bigtriangledown g_1 \left ( \hat{x} \right)= \left ( 4,2 \right)$ i

$\bigtriangledown g_2\left ( \hat{x} \right ) =\left ( 1,2 \right )$

Zatem umieszczając te wartości w pierwszym warunku warunków Karusha-Kuhna-Tuckera, otrzymujemy -

$u_1=\frac{1}{3}$ i $u_2=\frac{2}{3}$

Zatem warunki Karush-Kuhn-Tuckera są spełnione.

Metoda największego spadku

Ta metoda jest również nazywana metodą Gradientową lub metodą Cauchy'ego. Ta metoda obejmuje następującą terminologię -

$$x_{k+1}=x_k+\alpha_kd_k$$

$d_k= - \bigtriangledown f\left ( x_k \right )$ lub $ d_k= -\frac{\bigtriangledown f\left ( x_k \right )}{\left \| \bigtriangledown f\left ( x_k \right ) \right \|}$

Pozwolić $\phi \left (\alpha \right )=f\left ( x_k +\alpha d_k\right )$

Poprzez różnicowanie $\phi$ i zrównując ją z zerem, możemy otrzymać $\alpha$.

Więc algorytm wygląda następująco -

• Zainicjuj $x_0$,$\varepsilon_1$,$\varepsilon_2$ i nastaw $k=0$.

• Zestaw $d_k=-\bigtriangledown f\left ( x_k \right ) $lub $d_k=-\frac{\bigtriangledown f\left (x_k \right )}{\left \|\bigtriangledown f\left (x_k \right ) \right \|}$.

• odnaleźć $\alpha_k$ tak, że minimalizuje $\phi\left ( \alpha \right )=f\left ( x_k+\alpha d_k \right )$.

• Zestaw $x_{k+1}=x_k+\alpha_kd_k$.

• Jeśli $ \ left \ | x_ {k + 1-x_k} \ right \ | <\ varepsilon_1 $ lub$\left \| \bigtriangledown f\left ( x_{k+1} \right ) \right \| \leq \varepsilon_2$przejdź do kroku 6, w przeciwnym razie ustaw $k=k+1$ i przejdź do kroku 2.

• Optymalnym rozwiązaniem jest $\hat{x}=x_{k+1}$.

Metoda Newtona

Metoda Newtona działa na następującej zasadzie -

$f\left ( x \right )=y\left ( x \right )=f\left ( x_k \right )+\left ( x-x_k \right )^T \bigtriangledown f\left ( x_k \right )+\frac{1}{2}\left ( x-x_k \right )^T H\left ( x_k \right )\left ( x-x_k \right )$

$\bigtriangledown y\left ( x \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x-x_k \right )$

W $x_{k+1}, \bigtriangledown y\left ( x_{k+1} \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x_{k+1}-x_k \right )$

Dla $x_{k+1}$ za optymalne rozwiązanie $\bigtriangledown y\left ( x_k+1 \right )=0$

A zatem, $x_{k+1}=x_k-H\left ( x_k \right )^{-1} \bigtriangledown f\left ( x_k \right )$

Tutaj $H\left ( x_k \right )$ powinna być inna niż liczba pojedyncza.

Stąd algorytm wygląda następująco -

Step 1 - Inicjalizuj $x_0,\varepsilon$ i nastaw $k=0$.

Step 2 - znajdź $H\left ( x_k \right ) \bigtriangledown f\left ( x_k \right )$.

Step 3 - Znajdź system liniowy $H\left ( x_k \right )h\left ( x_k \right )=\bigtriangledown f\left ( x_k \right )$ dla $h\left ( x_k \right )$.

Step 4 - znajdź $x_{k+1}=x_k-h\left ( x_k \right )$.

Step 5- Jeśli $ \ left \ | x_ {k + 1} -x_k \ right \ | <\ varepsilon $ lub$\left \| \bigtriangledown f\left ( x_k \right ) \right \| \leq \varepsilon$ następnie przejdź do kroku 6, w przeciwnym razie ustaw $k=k+1$ i przejdź do kroku 2.

Step 6 - Optymalnym rozwiązaniem jest $\hat{x}=x_{k+1}$.

Metoda gradientu sprzężonego

Ta metoda służy do rozwiązywania problemów następujących typów -

$min f\left ( x \right )=\frac{1}{2}x^T Qx-bx$

gdzie Q jest dodatnio określoną macierzą nXn, a b jest stałą.

Dany $x_0,\varepsilon,$ obliczać $g_0=Qx_0-b$

Zestaw $d_0=-g_0$ dla $k=0,1,2,...,$

Zestaw $\alpha_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Q d_k}$

Obliczać $x_{k+1}=x_k+\alpha_kd_k$

Zestaw $g_{k+1}=g_k+\alpha_kd_k$

Obliczać $\beta_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Qd_k}$

Obliczać $x_{k+1}=x_k+\alpha_kd_k$

Zestaw $g_{k+1}=x_k+\alpha_kQd_k$

Obliczać $\beta_k=\frac{g_{k+1}^{T}g_{k+1}}{g_{k}^{T}gk}$

Zestaw $d_{k+1}=-g_{k+1}+\beta_kd_k$.