Podstawowe typy sygnałów
Oto kilka podstawowych sygnałów:
Funkcja kroku jednostkowego
Funkcja kroku jednostkowego jest oznaczona przez u (t). Jest zdefiniowany jako u (t) = $ \ left \ {\ begin {matrix} 1 & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right. $

- Jest używany jako najlepszy sygnał testowy.
- Obszar pod funkcją kroku jednostkowego to jedność.
Funkcja impulsów jednostkowych
Funkcja impulsu oznaczona jest przez δ (t). i jest zdefiniowany jako δ (t) = $ \ left \ {\ begin {matrix} 1 & t = 0 \\ 0 & t \ neq 0 \ end {matrix} \ right. $

$$ \ int _ {- \ infty} ^ {\ infty} δ (t) dt = u (t) $$
$$ \ delta (t) = {du (t) \ ponad dt} $$
Sygnał rampy
Sygnał rampy jest oznaczony przez r (t) i jest zdefiniowany jako r (t) = $ \ left \ {\ begin {matrix} t & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right . $

$$ \ int u (t) = \ int 1 = t = r (t) $$
$$ u (t) = {dr (t) \ ponad dt} $$
Obszar pod rampą jednostki to jedność.
Sygnał paraboliczny
Sygnał paraboliczny można zdefiniować jako x (t) = $ \ left \ {\ begin {matrix} t ^ 2/2 & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right. $
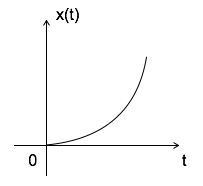
$$ \ iint u (t) dt = \ int r (t) dt = \ int t dt = {t ^ 2 \ over 2} = sygnał paraboliczny $$
$$ \ Rightarrow u (t) = {d ^ 2x (t) \ over dt ^ 2} $$
$$ \ Rightarrow r (t) = {dx (t) \ over dt} $$
Funkcja Signum
Funkcja Signum jest oznaczona jako sgn (t). Jest zdefiniowany jako sgn (t) = $ \ left \ {\ begin {matrix} 1 & t> 0 \\ 0 & t = 0 \\ -1 & t <0 \ end {matrix} \ right. $

Sygnał wykładniczy
Sygnał wykładniczy ma postać x (t) = $ e ^ {\ alpha t} $.
Kształt wykładniczy można zdefiniować za pomocą $ \ alpha $.
Case i: jeśli $ \ alpha $ = 0 $ \ to $ x (t) = $ e ^ 0 $ = 1

Case ii:jeśli $ \ alpha $ <0 ie -ve then x (t) = $ e ^ {- \ alpha t} $. Kształt nazywa się rozkładającym się wykładnikiem.

Case iii:jeśli $ \ alpha $> 0 ie + ve to x (t) = $ e ^ {\ alpha t} $. Kształt nazywa się podnoszeniem wykładniczym.

Sygnał prostokątny
Niech będzie oznaczony jako x (t) i zdefiniowany jako

Trójkątny sygnał
Niech będzie oznaczony jako x (t)

Sygnał sinusoidalny
Sygnał sinusoidalny ma postać x (t) = A cos ($ {w} _ {0} \, \ pm \ phi $) lub A sin ($ {w} _ {0} \, \ pm \ phi $ )
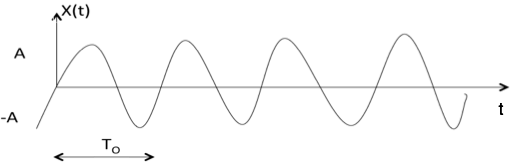
Gdzie T 0 = 2 $ \ pi \ ponad {w} _ {0} $
Funkcja Sinc
Jest oznaczany jako sinc (t) i definiowany jako sinc
$$ (t) = {sin \ pi t \ over \ pi t} $$
$$ = 0 \, \ text {for t} = \ pm 1, \ pm 2, \ pm 3 ... $$

Funkcja próbkowania
Jest oznaczony jako sa (t) i zdefiniowany jako
$$ sa (t) = {sin t \ over t} $$
$$ = 0 \, \, \ text {for t} = \ pm \ pi, \, \ pm 2 \ pi, \, \ pm 3 \ pi \, ... $$
