Właściwości transformacji Z

Z-Transform ma następujące właściwości:

Właściwość liniowości

Jeśli $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

i $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Następnie własność liniowości stwierdza, że

$ a \, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a \, X (Z) + b \, Y (Z) $

Właściwość przesunięcia w czasie

Jeśli $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Następnie własność przesunięcia w czasie stwierdza to

$ x (nm) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z) $

Mnożenie przez właściwość wykładniczej sekwencji

Jeśli $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Następnie mnożenie przez właściwość sekwencji wykładniczej stwierdza, że

$ a ^ n \,. x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $

Właściwość Time Reversal

Jeśli $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Następnie własność odwrócenia czasu to stwierdza

$ x (-n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z) $

Zróżnicowanie w dziedzinie Z LUB Mnożenie przez właściwość n

Jeśli $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Następnie mnożenie przez n lub różnicowanie we własności domeny z stwierdza, że

$ n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ over dZ ^ K} $

Własność splotu

Jeśli $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

i $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Następnie własność splotu stwierdza, że

$ x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z) $

Właściwość korelacji

Jeśli $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

i $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Następnie własność korelacji to stwierdza

$ x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1}) $

Twierdzenia o wartości początkowej i końcowej

Twierdzenia o wartości początkowej i końcowej transformacji z są zdefiniowane dla sygnału przyczynowego.

Twierdzenie o wartości początkowej

Dla sygnału przyczynowego x (n) twierdzenie o wartości początkowej stwierdza, że

$ x (0) = \ lim_ {z \ to \ infty} ⁡X (z) $

Służy do znalezienia początkowej wartości sygnału bez wykonywania odwrotnej transformacji z

Twierdzenie o wartości końcowej

Dla sygnału przyczynowego x (n) twierdzenie o wartości końcowej stwierdza, że

$ x (\ infty) = \ lim_ {z \ do 1} [z-1] ⁡X (z) $

Służy to do znalezienia końcowej wartości sygnału bez wykonywania odwrotnej transformacji z.

Region konwergencji (ROC) transformacji Z

Zakres zmienności z, dla którego zbiega się transformata z, nazywany jest regionem zbieżności transformaty z.

Własności ROC transformacji Z

ROC transformacji z jest oznaczony okręgiem w płaszczyźnie z.
ROC nie zawiera tyczek.
Jeśli x (n) jest sekwencją przyczynową o skończonym czasie trwania lub sekwencją prawostronną, to ROC jest całą płaszczyzną z, z wyjątkiem z = 0.
Jeśli x (n) jest sekwencją przeciwprzyczynową o skończonym czasie trwania lub sekwencją lewostronną, to ROC jest całą płaszczyzną z, z wyjątkiem z = ∞.
Jeśli x (n) jest sekwencją przyczynową o nieskończonym czasie trwania, ROC jest poza okręgiem o promieniu aie | z | > a.
Jeśli x (n) jest sekwencją antyprzyczynową o nieskończonym czasie trwania, ROC jest wnętrzem koła o promieniu aie | z | <a.
Jeśli x (n) jest dwustronną sekwencją o skończonym czasie trwania, to ROC jest całą płaszczyzną z, z wyjątkiem z = 0 iz = ∞.

Koncepcję ROC można wyjaśnić następującym przykładem:

Example 1: Znajdź transformację z i ROC dla $ a ^ nu [n] + a ^ {-} nu [-n-1] $

$ ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ ponad Za} + {Z \ ponad Z {-1 \ ponad a}} $

$$ ROC: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ over a} $$

Wykres ROC ma dwa warunki jako a> 1 i a <1, ponieważ nie znasz a.

W tym przypadku nie ma kombinacji ROC.

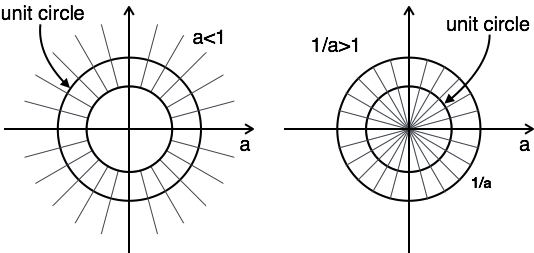
Tutaj kombinacja ROC pochodzi z $ a \ lt | z | \ lt {1 \ ponad a} $

Stąd w przypadku tego problemu transformacja z jest możliwa, gdy a <1.

Przyczynowość i stabilność

Warunek przyczynowości dla systemów LTI z czasem dyskretnym jest następujący:

System LTI z dyskretnym czasem jest przyczynowy, gdy

ROC znajduje się na zewnątrz skrajnego bieguna.
W funkcji przenoszenia H [Z] kolejność licznika nie może być większa niż kolejność mianownika.

Warunek stabilności dla systemów LTI z czasem dyskretnym

Dyskretny system LTI jest stabilny, gdy

jego funkcja systemowa H [Z] obejmuje okrąg jednostkowy | z | = 1.
wszystkie bieguny funkcji przenoszenia leżą wewnątrz koła jednostkowego | z | = 1.

Transformacja Z sygnałów podstawowych

x (t)	X [Z]
$ \ delta $	1
$ u (n) $	$ {Z \ ponad Z-1} $
$ u (-n-1) $	$ - {Z \ ponad Z-1} $
$ \ delta (nm) $	$ z ^ {- m} $
$ a ^ nu [n] $	$ {Z \ ponad Za} $
$ a ^ nu [-n-1] $	$ - {Z \ ponad Za} $
$ n \, a ^ nu [n] $	$ {aZ \ over \| Za \| ^ 2} $
$ n \, a ^ nu [-n-1] $	$ - {aZ \ over \| Za \| ^ 2} $
$ a ^ n \ cos \ omega nu [n] $	$ {Z ^ 2-aZ \ cos \ omega \ over Z ^ 2-2aZ \ cos \ omega + a ^ 2} $
$ a ^ n \ sin \ omega nu [n] $	$ {aZ \ sin \ omega \ over Z ^ 2 -2aZ \ cos \ omega + a ^ 2} $