Raciocínio - Números binários codificados
O número que tem base 2 é conhecido como número binário. O número binário é formado por complementos de 0 e 1. Portanto, o número binário codificado consiste em dois processos. Um é a conversão de binário em decimal e outro é de decimal em binário.
Números decimais
Para saber o que binary numberou seja, primeiro temos que saber sobre os números decimais. Portanto, o número decimal consiste em dez dígitos (ou seja, 0,1,2,3,4,5,6,7,8,9). Qualquer sistema decimal pode ser representado usando esses números. Por exemplo, uma sequência de dígitos é 2, 4, 6 e 8. Fazemos isso da seguinte maneira -
2468 = 2 × 10 3 + 4 × 10 2 + 6 × 10 1 + 8 × 10 0
= 2468
Note- Obtemos o valor dos números, neste caso, multiplicando diferentes dígitos da sequência por potências de 10 e somando. Aqui, esse 10 é chamado de base ou raiz. Portanto, em um sistema decimal, nossa base é 10.
Números Binários
Usamos dez dígitos para representar um decimal number; assim, usamos apenas dois dígitos para representar o número binário. Qualquer número pode ser representado usando esses dois dígitos, ou seja, 0 e 1.
O exemplo de um número binário é - 1101. Aqui, 4 dígitos estão presentes na seqüência de dígitos - 1, 1, 0, 1. Obtemos o valor da seguinte maneira.
1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1 = 13
Assim, o número binário representa treze no sistema decimal. O valor pode ser determinado pormultiplying different digits de sequência por potências de 2 e somando.
Conventional method - No exemplo acima, vemos que para obter o valor de qualquer número binário, usamos a seguinte regra -
O primeiro dígito da direita é multiplicado por 2 0 = 1
O segundo dígito da direita é multiplicado por 2 1 = 2
O terceiro dígito da direita é multiplicado por 2 2 = 4
Da mesma forma, o enésimo dígito da direita é multiplicado por 2 n − 1
Finalmente, todos esses são adicionados.
For Example - Converta os seguintes números binários em números decimais.
A - 1010
B - 1111
C - 100
D - 10.000
Solution -
A - 1010 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
B - 1111 = 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
C - 100 = 1 × 2 2 + 0 × 2 1 + 0 × 2 0
D - 10000 = 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 0 × 2 0
Método mais rápido
Step I- Começando com o dígito direito do número dado, escreva 1, 2, 4, 8, 16, 32 ……. e assim por diante abaixo de cada dígito conforme você avança para a esquerda.
Step II- Ignore os números abaixo de 0s. Adicione todos os números abaixo de 1s.
Vamos resolver o exemplo 1 por este método.
A - 1010
Usaremos 1,2,4,8 porque aqui 4 dígitos estão presentes.
Nós temos,
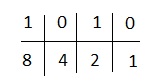
4 e 1 ficam abaixo dos zeros. Nós os ignoramos e adicionamos o restante. Obtemos 8 + 2 = 10
Assim podemos resolver outros números.
O número decimal pode ser convertido em binário pelo método de successive divisions. Cada vez de divisão, o dividendo é dividido por 2. O lembrete é anotado e o quociente se torna o próximo dividendo, que é novamente dividido por 2. O processo é repetido até que nenhuma divisão seja possível.
Por exemplo - converter 17 em número binário -
Divida 17 por 2 até que nenhuma divisão seja possível.
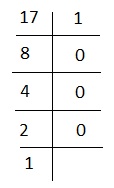
Portanto, a forma binária de 17 é 10001.
Direction (Q. 1-4) − Study the following question and give the answer.
Em um determinado código, o símbolo para 0 é + e para 1 é #. Nenhum número ou símbolo é maior do que 1. O valor do símbolo para 1 dobra a si mesmo toda vez que ele muda uma posição para a esquerda.
'0' é representado como +
'1' é descrito como #
'2' é descrito como # +
'3' é descrito como ##
'4' é descrito como # ++ e assim por diante
1 - Qual das seguintes opções representará 11?
Options -
A - # + ##
B - + ## +
C - ## ++
D - # + # ++
E - nenhum desses
Answer - Opção A
Explanation - Para obter o equivalente a 11, usamos o método de divisão sucessiva por 2.

Portanto, a forma binária será 10111. Substituindo 1 e 0 por # e + teremos # + ##.
2 - Qual dos seguintes representará 8?
Options -
A - ## ++
B - + ## +
C - ## ++
D - ++ ##
E - nenhum desses
Answer - Opção E
Explanation - para 8, temos-
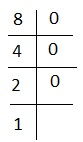
ou seja, 1000 ou # +++. A escolha correta é 5.
3 - Qual dos seguintes será representado por ## + #?
Options -
A - 8
B - 11
C - 13
D - 12
E - nenhum desses
Answer - Opção E
Explanation- ## + # = 1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 15
4 - Qual dos seguintes números será representado por # +++ #?
Options -
A - 22
B - 31
C - 14
D - 17
E - nenhum desses
Answer - Opção D
Explanation - # + + + # = 10001
= 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
= 16 + 1 = 17
Os sistemas binários têm base 2, o sistema decimal tem base 10 e o sistema terciário tem base 3, enquanto o sistema octal tem base 8. No caso do terciário, temos três dígitos para representar os números. São 0, 1 e 2. Neste caso, os números serão convertidos em decimais multiplicando com as potências apropriadas de 3.
For Example -
(12012) 3 = 1 × 3 4 + 2 × 3 3 + 0 × 3 2 + 1 × 3 1 + 2 × 3 0 = (104) 3