Raciocínio - Silogismo
O significado de silogismo dado pelos gregos é Deduction. É uma espécie de argumentação lógica.
Definição de alguns termos importantes
Existem alguns termos fornecidos abaixo que têm papel importante na resolução de problemas de silogismo.
Proposition- proposição é uma frase que faz afirmações. A proposição consiste em 3 partes: a) sujeito, b) predicado ec) a relação entre sujeito e predicado. Algumas proposições são fornecidas abaixo.
- Todas as costas são praias.
- Nenhum aluno é honesto.
- Alguns documentos são secretos.
Subject and Predicate- Assunto é aquela parte sobre a qual algo está sendo dito. Por outro lado, predicado é a parte que se relaciona com o sujeito. Por exemplo - das proposições acima, costas, alunos, documentos são assuntos, enquanto praias, honestos e secretos são predicados.
Tipos de proposições categóricas
Universal Proposition- A proposição universal é aquela que inclui o sujeito totalmente ou o exclui inteiramente. Por exemplo, nenhum aluno é inteligente. A proposição universal é ainda classificada na seguinte -
Universal positive proposition - Quando o formulário é all X are Yentão é chamada de proposição positiva. Geralmente é denotado por letrasA.
Universal negative proposition - Quando o formulário é no X are T, então é chamado de proposição negativa. É denotado porE.
Particular proposition- É a proposição que mostra o sujeito parcialmente ou o exclui parcialmente, mas não completamente. Por exemplo, alguns gatos são de algodão. Também é dividido nos seguintes tipos -
Particular positive proposition - Formulários como some X are Usão chamados de proposições positivas particulares. Eles são codificados comoI.
Particular negative proposition - Formulários como Some T are not P por exemplo, some cats are not coils é chamada de proposição negativa particular e codificada como O.
Mediate inference- Aqui a conclusão é tirada de duas afirmações. Exemplo - “todos os lábios são espirais” e “todas as bolas são morcegos”. Portanto, a conclusão será “todos os lábios são bobinas”.
Immediate inference- Aqui a conclusão será tirada de apenas uma proposição. Por exemplo, se a afirmação for “todos os professores são Deus”, a conclusão será “alguns professores são Deus”.
Dois métodos importantes de inferência imediata
Esses métodos incluem conversão, contraposição, etc.
Implications- Suponha que, dado que “todos os gatos são praias”, isso mostra que a conclusão “alguns gatos são praias” é verdadeira. Portanto, se uma dada proposição é da categoria A, ela também mostra que a conclusão do tipo I deve ser verdadeira.
Conversion - Consiste em 2 etapas.
Step 1 - O sujeito será convertido em predicado e vice-versa.
Step 2 - A proposição dada será alterada em conformidade.
For Example −
Statements- Todos os gatos são racks. Todas as malas são prateleiras. Algumas bolsas são bolsas.
Conclusions -
1. Alguns gatos são bolsas.
2. Algumas prateleiras são gatos.
3. Algumas prateleiras são bolsas.
A - Apenas 1
B - Apenas 2 e 3
C - Apenas 1 e 2
D - Apenas 1 e 3
Solution −
Resposta - Opção B
A forma pictórica de representar proposições é formulada por Euler. Existem quatro maneiras pelas quais a relação poderia ser feita de acordo com quatro proposições.
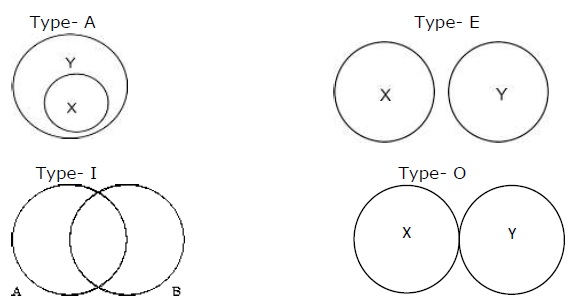
Tipo - A significa “Todos os X são Y”, Tipo - E significa “Nenhum X é Y”, Tipo - I significa “Alguns A são B” e Tipo - O significa “Alguns X não são Y”.
For Example −
Statements −Algumas câmeras são laptops.
Alguns laptops são telefones.
Alguns telefones são tablets.
Conclusions −
I - Pelo menos alguns tablets são câmeras
II - Existe a possibilidade de que todos os tablets sejam laptops
III - Nenhum dos tablets é laptop
Solution −
Diagrama de Círculo -
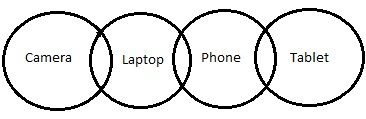
Conforme o diagrama acima,
A conclusão III segue. Mas a palavra "possibilidade" foi mencionada na declaração. Portanto, vamos verificar as possibilidades.
O novo diagrama será -
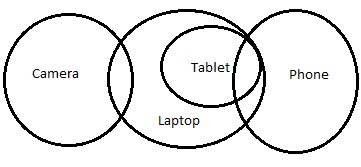
Mas, neste caso, a conclusão III não segue. Segue-se a conclusão II ou a conclusão III.