Raciocínio - Diagramas de Venn lógicos

Introdução

É um processo de mostrar relacionamento complexo entre 2-3 categorias em diagrama por meio de várias restrições geométricas. A interseção entre duas estruturas geométricas indica que elas têm algo em comum e o isolamento total indica exatamente o oposto disso. Embora a teoria pareça complexa vista de cima, uma compreensão básica de vários tipos de exemplos de casos ajudará a resolver as próximas questões com mais facilidade.

Fundamentos

Dê uma olhada em vários casos possíveis de diagrama de Venn e saiba quando ele é aplicável. Entre as três colunas, a primeira mostra o tipo de diagrama de Venn, a segunda é para descrição e a terceira mostra um exemplo para dar uma imagem clara da descrição.

Diagrama de Venn	Casos aplicáveis	Exemplo
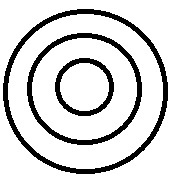
	Haverá uma série de subcasos, um abaixo do outro.	Cor> Verde> verde claro. A cor verde clara é uma sub-parte da cor verde e ambas pertencem ao grupo de cores.
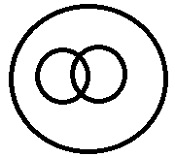
	Uma categoria principal, sob ela duas subcategorias e ambas têm algumas semelhanças entre si.	Líquidos> Gasolina, diesel. Aqui, ambos são inflamáveis por natureza, portanto, têm semelhanças.
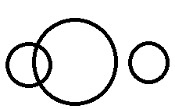
	Uma categoria pode ter uma subcategoria. Ambos satisfazem parcialmente algumas condições (nem sempre).	Vegetal> Capsicum> Vermelho. Alguns pimentões são vermelhos e outros vegetais.
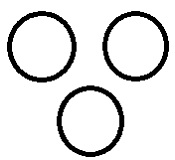
	Entre três seções diferentes, duas podem ter algumas propriedades comuns que não correspondem à terceira.	Ator> Diretor> Rainha. Do exposto, o ator e o diretor estão mostrando masculinidade, portando algumas propriedades comuns que são exatamente opostas ao Queen.
	Três seções sem característica comum.	Árvore> Irritado> Café. Não há lógica em encontrar qualquer aspecto comum entre os três termos acima.
	Há uma chance de encontrar um lugar comum que satisfaça todas as propriedades de três seções individuais.	Mãe> Madrasta> Cunhada. Uma única mulher pode ser todas as opções acima mencionadas simultaneamente.
	Isso é particular para aqueles casos em que de três seções, duas estão inter-relacionadas como relação pai-filho, enquanto a terceira não tem relação com eles.	Árvore> bananeira> Irritada. Todos nós sabemos que a bananeira vem na categoria de árvore, mas a emoção ”Irritada” não tem nada a ver com essas 2 palavras.

Outro tipo de questão que frequentemente surge neste capítulo é a interseção de várias estruturas geométricas. Cada estrutura geométrica terá alguns elementos próprios e cada estrutura terá algumas características ou classes. A intersecção de duas ou mais estruturas dará um amálgama que mudará a propriedade de cada elemento anterior por algo novo. Temos que identificar isso e responder de acordo com as opções fornecidas.

Amostras

Cinco pessoas são numeradas e possuem algumas características. Estude o diagrama para responder corretamente.