Raciocínio - Cubo e Cubóide
Hoje em dia, questões baseadas em 'Cubos e Cuboids' estão sendo feitas em quase todos os exames competitivos. Esses problemas são muito frequentes em vários exames competitivos.
Os métodos descritos abaixo são simples, mas elegantes. Eles devem ser muito fáceis de entender e com um pouco de prática você deve dominá-los. Um cubo é um sólido tridimensional com 6 faces, 12 arestas e cantos. Todas as arestas de um cubo são iguais e todas as faces são quadradas. Essa é uma figura sólida que tem 6 faces; cada rosto sendo um quadrado é chamadoa cube. Se cada uma das seis faces for um retângulo, é chamadocuboid. Um cubóide também é chamado derectangular parallelepiped.
As perguntas feitas no cubo e cubóides podem ser dos seguintes tipos.
Tipo I
Várias visualizações de um cubo completo são fornecidas e você deve descobrir qual parte do cubo está exatamente abaixo de uma determinada parte.
Tipo II
Um cubo aberto é fornecido e você tem que prever como ele ficará quando for fechado em um cubo.
Tipo III
Um cubo não podia ser envernizado ou em algumas de suas faces com a mesma cor ou cores diferentes e depois cortado em um determinado número especificado de peças idênticas. Então, a questão da forma - "quantos cubos pequenos têm 2 faces envernizadas?" “Quantos cubos pequenos têm apenas uma face envernizada?” etc.
Existem dois tipos de problemas que aparecem no exame. No início, você recebe várias visualizações de umcomplete cube, e você deve indicar qual parte do cubo está exatamente abaixo de uma parte específica. Em outro tipo, você recebe umopened-up cube, e você tem que prever como será quando for fechado em um cubo.
For Example -
Várias faces de um cubo são mostradas abaixo -

Qual número ficaria oposto a 2?
A - 1
B - 6
C - 5
D - 4
A abordagem fundamental é a seguinte -
Tipo I
A fundamental rule: Opposite cannot be together;
Sempre que vemos um cubo, com apenas três de suas faces visíveis para nós, nunca podemos ver duas faces opostas juntas. Com todas essas regras, podemos resolver facilmente o tipo de problema discutido acima. Na pergunta acima, onde temos que encontrar a face oposta de uma face particular, podemos eliminar aquelas faces que ocorreram junto com X em qualquer vista. Assim, podemos eliminar todas as outras opções e o restante será nossa resposta.
Neste ponto, você deve passar pelo parágrafo anterior mais uma vez e ver se entendeu o conceito. Depois disso, você deve tentar resolver o exemplo acima e ver se consegue aplicar o conceito discutido acima. No entanto, você descobre que não entendeu o conceito totalmente, sem problemas. Continue lendo esta seção. As coisas ficarão claras quando você terminar a seção. Com a regra fundamental anterior em mente, você pode resolver o tipo de questão acima.
Para a pergunta, a regra é suficiente por si só. Depois disso, você pode resolvê-lo mais rapidamentethree secondary rules.
Solution for above example -
No exemplo dado, temos que encontrar a face oposta a 2. Agora, na primeira figura, 2 está aparecendo junto com 1 e 3. Isso significa que nem 1 nem 3 podem ser opostos a 2. Isso significa que oposto de 1 podemos tenha 4 ou 5 ou 6. Da mesma forma, ao lado de 3 podemos ter 4, 5 ou 6. Agora, olhe para a segunda figura. Aqui, 3 e 1 ocorrem junto com 5. Isso significa que 5 é oposto a nem 3 nem 1. Então, isso significa que 4 ou 6 é oposto a 1 e outro é oposto a 3, então 5 deve ser oposto a 2. Portanto, 5 é correto responda.
Algumas regras mais rápidas
Agora você deve ter entendido o truque básico para resolver essas questões. O truque é eliminar as escolhas que não são possíveis. Para isso, recorre-se à regra fundamental que diz que, se duas faces são opostas uma à outra, não é possível a sua ocorrência simultânea em uma vista do cubo. No entanto, nas competições preciosas de hoje, apenas o conceito não serve. Você deve ser capaz de resolver uma questão rapidamente. Existem algumas regras secundárias para resolver questões.
Rule I- Vamos chamar essa figura de X, o oposto do qual você deve encontrar. Suponha que em qualquer vista do cubo, X apareça com Y e Z. Junto com uma terceira figura (digamos A), então X será oposto a A.
Por exemplo, você deve encontrar a face oposta a 2. (Este é o nosso X). Agora, 2 aparece em uma figura junto com 1 e 3. (Y e Z). Também 1 e 3 aparecem juntos em mais uma figura, junto com 5. (Isso é A). Portanto, 2 deve ser oposto a 5.
Rule II- Temos que encontrar a face oposta de 'X'. Suponha que em qualquer vista do cubo, X apareça com Y e Z. Agora, suponha que Y e Z não apareçam juntos em mais vistas, mas aparecem separadamente em duas ou mais vistas diferentes. Então, a figura comum entre as duas outras vistas nas quais Y e Z aparecem separadamente, será a figura oposta a X.
Rule III- Vamos chamar a figura X, o oposto do qual você tem que encontrar. Agora, suponha que X apareça em duas vistas e nessas duas vistas quatro figuras diferentes sejam vistas com X. Então, a única figura não vista com X nessas duas vistas deve ser oposta a X.
Summary- Você deve manter a regra fundamental no fundo de sua mente e, em seguida, aplicar três regras secundárias para respostas rápidas. Toda a abordagem pode ser resumida no diagrama a seguir.
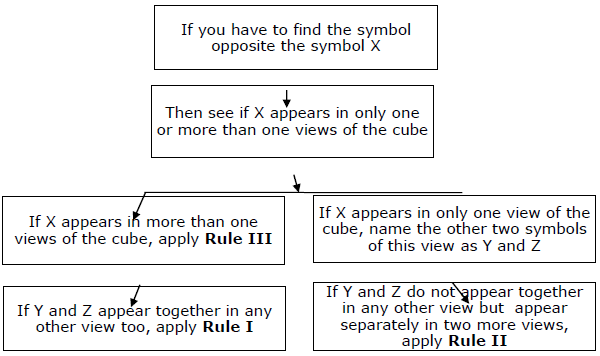
Tipo II
Neste tipo, usamos regra fundamental. Esta regra nos ajuda a eliminar as combinações em que faces opostas são mostradas em uma única visualização. Portanto, isso levará à eliminação de uma escolha, desde que saibamos como determinar qual face será oposta uma à outra, olhando para o “opened-up cube”. Para este propósito, existe uma regra muito simples que você pode dizer olhando para oopened-up cube, quais faces ficarão opostas apenas ao olhar para elas.
A regra é fornecida abaixo;
Third is opposite rule -
Quando você quiser descobrir a face oposta de uma face (digamos X), nas figuras I, II, III; um cubo aberto é dado. Temos que descobrir quais faces estão opostas uma à outra quando o cubo é fechado.
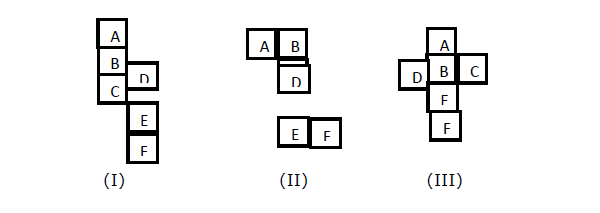
Explanation -
Na figura (I), a terceira figura para A é C. Portanto, A é oposto a C. Portanto, D e F serão opostos. B e E serão opostos.
Na figura (II), B é o terceiro a D, então B será oposto a D. Da mesma forma, C será oposto a E e A será oposto a F.
Na figura (III), A é oposto a E, B é oposto a F. Portanto, C é oposto a D.
Steps to solve problem
Agora podemos resolver questões desse tipo. Sabemos como encontrar a face oposta olhando para umOpened-up cube. Também sabemos que em qualquer visão do cubo, faces opostas não podem estar juntas. Portanto, combinando duas regras, podemos resolver problemas facilmente.
Resumo
Com isso, fica encerrada a discussão de como solucionar questões do tipo II. Você tem que usar a terceira regra para determinar quais faces são opostas entre si. O diagrama a seguir fornecerá as informações completas sobre essa abordagem.

Tipo III
Counting of Cubes (when a varnished solid cube is cut);
Na seção anterior, discutimos o problema de encontrar a face oposta de um cubo. Existe um outro tipo de questão relacionada com os cubos em que um cubo maior com cores diferentes envernizadas em lados diferentes, é dividido em vários cubos menores e você deve encontrar o número de cubos tendo apenas um lado envernizado ou dois lados envernizados.
Format of this problem -
Example -
Um cubo é envernizado com três cores verde, azul e vermelho em seus lados, com todas as cores envernizadas nas duas faces opostas do cubo. Agora o cubo está dividido em 64 cubos de tamanhos iguais. Com base nessas informações, responda às seguintes perguntas -
1. Quantos cubos têm duas faces envernizadas e as faces restantes não envernizadas?
A - 18
B - 20
C - 22
D - 24
2. Quantos cubos têm apenas um lado envernizado (com a cor verde ou azul apenas)
A - 4
B - 24
C - 16
D - 12
3. Quantos cubos não têm as faces envernizadas?
A - 0
B - 8
C - 12
D - 64