Raciocínio - Dedução Lógica
A dedução lógica é um capítulo importante, pois muitas questões fáceis e de recuperação de notas deste capítulo estão incluídas em vários exames competitivos. Neste capítulo, discutiremos dois métodos para resolver esses problemas -
- Método de silogismo
- Método de diagrama de Venn
Fundamentos
Se houver duas afirmações, então o silogismo será a melhor maneira de resolver o problema, mas se o número de afirmações for maior do que duas, escolha o método do diagrama de Venn. Às vezes, declarações e conclusões são derivadas de fatos geralmente aceitos, mas também podem ser não lógicas. Por exemplo -
a) Algumas cadeiras são portas.
b) Todos os homens são mulheres
c) Nenhum leite é branco
Para chegar à conclusão, o pensamento abstrato é necessário. É preciso entender o sentido lógico da frase e, então, responder às conclusões de acordo. Cada afirmação precisa ser considerada verdadeira, então temos que verificar se as conclusões estão logicamente seguindo as afirmações.
Qualificadores
Estas são algumas das palavras elementares usadas para descrever o quanto uma coisa é semelhante ou diferente de outra. Exemplos de alguns dos qualificadores são “Todos”, “Alguns”, “Alguns não” etc.
Conceito de diagrama de Venn
Por outro lado, o diagrama de Venn é um processo em que podemos representar uma frase ou declaração na forma de figuras geométricas. Todas as declarações fornecidas são plotadas em possíveis diagramas de Venn. Em seguida, todas as conclusões são verificadas com esses diagramas. Qualquer conclusão que satisfaça todos os diagramas de Venn será considerada uma conclusão válida.
| Afirmações | Diagramas de Venn Correspondentes |
|---|---|
| Todos A são B |
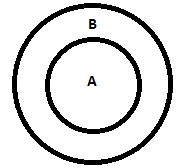
|
| Alguns A são B (OU) Alguns A não são B |
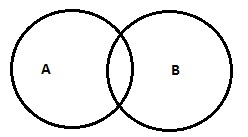
|
| Nenhum A é B |
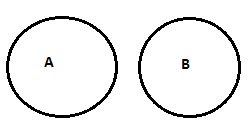
|
Vamos dar um exemplo simples para entendê-lo de uma maneira muito melhor.
Sample − 1
Statements -
Todos os engenheiros são tolos. Todos os tolos são médicos. Todos os médicos são pobres.
Conclusions -
I. Alguns pobres são tolos.
II. Alguns pobres são engenheiros.
Options -
A - Só eu é válido
B - Apenas II é válido
C - Ambas as afirmações são válidas
D - Nenhuma das afirmações é válida
Answer - Opção C
Explanation -
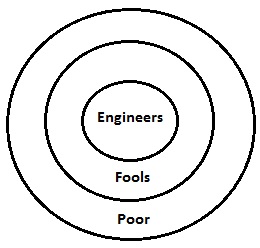
O diagrama de Venn para as declarações fornecidas é desenhado acima. Ele mostra todas as declarações em diagrama em um só lugar. Agora, se discutirmos sobre as conclusões uma por uma, tudo ficará claro.
Aqui, os tolos são um subconjunto dos pobres. Portanto, é um fato óbvio que alguns pobres serão tolos. Portanto, a conclusão I é válida. Da mesma forma, a conclusão II é válida porque os engenheiros também são um subconjunto dos pobres. Portanto, ambas as declarações serão válidas.
Sample − 2
Statements -
Alguns teclados são Mouse. Alguns ratos são rádios.
Conclusions -
I. Alguns teclados são rádios.
II. Alguns rádios são teclados
III. Todos os rádios são Mouse.
IV. Todos os ratos são teclados.
Options -
A - Apenas a conclusão I é válida
B - Apenas a conclusão II é válida
C - I ou II é válido
D - Nenhuma das conclusões é válida
E - Ambos I e II são válidos
Answer - Opção D
Explanation - Visto que ambas as declarações são particulares, nenhuma conclusão definitiva é válida.
Sample − 3
Statements -
Todos os alunos estão sóbrios. Todos os alunos são travessos.
Conclusions -
I. Todos os desobedientes são sóbrios ou vice-versa.
II. Algumas pessoas sóbrias são travessas.
III. Geralmente desobedientes são sóbrios.
IV. Crime e culpa andam juntos.
Options -
A - Apenas a conclusão I é válida
B - Apenas a conclusão II é válida
C - I ou II é válido
D - Nenhum dos I ou II é válido
E - Ambos I e II são válidos
Answer - Opção B
Explanation- Uma vez que o termo intermediário 'alunos' é distribuído duas vezes nas falas, a conclusão não pode ser ampla. Portanto, é válido que 'Algumas pessoas sóbrias são travessas'. Portanto, II é válido.