จักรวาลวิทยา - รังสีครอบงำจักรวาล
ในบทนี้เราจะพูดถึงการแก้สมการของฟรีดมันน์ที่เกี่ยวข้องกับการแผ่รังสีที่ครอบงำจักรวาล ในตอนแรกเราเปรียบเทียบความหนาแน่นของพลังงานของสสารกับรังสี สิ่งนี้จะช่วยให้เราเห็นว่าเอกภพของเราถูกสสารครอบงำหรือถูกรังสีครอบงำ
ความหนาแน่นของพลังงานของการแผ่รังสี
การแผ่รังสีที่แพร่หลายในเอกภพปัจจุบันสามารถนำมาประกอบกับแหล่งกำเนิดของดาวฤกษ์ได้น้อยมาก แต่ส่วนใหญ่เกิดจาก CMB ที่เหลืออยู่ (พื้นหลังไมโครเวฟของจักรวาล)
ความหนาแน่นพลังงานของรังสี $ \ epsilon _ {\ gamma, 0} $ สามารถแสดงได้ดังนี้ -
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$
ที่นี่ a คือค่าคงที่ของการแผ่รังสีซึ่งมีนิพจน์ $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ เท่ากับ a = 7.5657 × 10−15erg\: cm−3 K−4. อุณหภูมิ T0 ที่เราพิจารณาที่นี่สอดคล้องกับตัวสีดำที่สอดคล้องกับ CMB
แทนที่ผลลัพธ์เรามี
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ times 10 ^ {- 13} erg \: cm ^ {- 3} $$
ความหนาแน่นของพลังงานของสสาร
ในการคำนวณต่อไปนี้เรามีสมมติฐานในการทำงานกับจักรวาลแบนและ K = 0 เราพิจารณาความหนาแน่นของพลังงานเป็น $ \ epsilon = \ rho c ^ 2 $ เราพิจารณาสิ่งต่อไปนี้ -
$$ \ rho_ {m, 0} c ^ 2 = 0.3 \ rho_ {c, 0} c ^ 2 = 0.3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} erg \: cm ^ {- 3} $$
$$ \ rho_ {b, 0} c ^ 2 = 0.03 \ rho_ {c, 0} c ^ 2 = 0.03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} erg \: cm ^ {- 3} $$
ดังนั้นจากการคำนวณข้างต้นเราจะเห็นว่าเราอาศัยอยู่ในเอกภพที่ถูกครอบงำด้วยสสาร สิ่งนี้สามารถรองรับได้จากข้อเท็จจริงที่ว่า CMB นั้นเย็นมาก เมื่อเรามองย้อนเวลากลับไปเราจะมีอุณหภูมิ CMB ที่ร้อนขึ้นและจะสามารถสรุปได้ว่าอาจมียุคที่เอกภพถูกรังสีครอบงำ
การเปลี่ยนแปลงของความหนาแน่นและสเกลแฟกเตอร์
สมการของไหลแสดงให้เราเห็นว่า -
$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$
ถ้าเราพิจารณาจักรวาลที่เต็มไปด้วยฝุ่นเราก็จะมี P = 0 เมื่อมองจากผลลัพธ์ก่อนหน้านี้เราจะถือว่าเอกภพถูกครอบงำด้วยรังสี
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$
ใช้ความสัมพันธ์แรงกดของ $ P_ {rad} = \ rho c ^ {2/3} $ เรามี -
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$
$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$
ในการทำให้เข้าใจง่ายขึ้นเรามี
$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$
$$ \ rho_ {rad} a ^ 4 = \: ค่าคงที่ $$
$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$
ผลลัพธ์ข้างต้นแสดงการแปรผันกำลัง4 thผกผันของ a กับ $ \ rho $
สิ่งนี้สามารถตีความได้ทางกายภาพว่า $ a ^ {- 3} $ เข้ามาจากการเปลี่ยนแปลงของปริมาณเมื่อมันเพิ่มขึ้น $ a ^ {- 1} $ ที่เหลือสามารถถือว่าเป็นพลังงานที่โฟตอนสูญเสียไปเนื่องจากการขยายตัวของพื้นที่ในจักรวาล (Cosmological redshift 1 + z = a -1 )
ภาพต่อไปนี้แสดงการเปลี่ยนแปลงของสสารและความหนาแน่นของรังสีตามเวลา
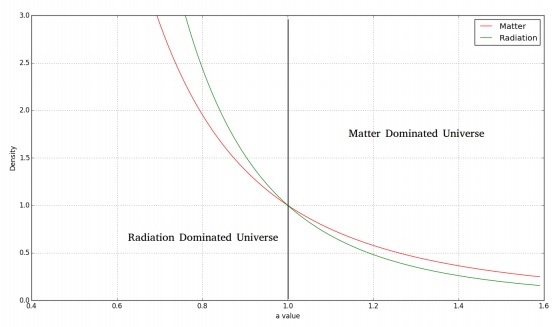
สำหรับเอกภพที่มีการแผ่รังสีแบนราบเราจะมีสมการฟรีดมันน์ดังนี้ -
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$
ในการทำให้เข้าใจง่ายและใช้วิธีแก้ปัญหากับสมการเชิงอนุพันธ์เรามี -
$$ (\ dot {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$
$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $$
ดังนั้นเราจึงมี -
$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$
จากสมการข้างต้นเราจะเห็นว่าอัตราการเพิ่มขึ้นของสเกลแฟคเตอร์นั้นน้อยกว่าของจักรวาลที่เต็มไปด้วยฝุ่น
สิ่งที่ต้องจำ
การแผ่รังสีที่แพร่หลายในเอกภพปัจจุบันสามารถนำมาประกอบกับแหล่งกำเนิดของดาวฤกษ์ได้น้อยมาก
สำหรับจักรวาลที่เต็มไปด้วยฝุ่นความดันเป็นศูนย์
CMB หนาวมาก