จักรวาลวิทยา - Robertson-Walker Metric
ในบทนี้เราจะเข้าใจรายละเอียดเกี่ยวกับเมตริกของ Robertson-Walker
แบบจำลองสำหรับสเกลแฟกเตอร์ที่เปลี่ยนแปลงตามเวลา
สมมติว่าโฟตอนถูกปล่อยออกมาจากกาแล็กซีอันไกลโพ้น ช่องว่างข้างหน้าสำหรับโฟตอนในทุกทิศทาง การขยายตัวของจักรวาลเป็นไปในทุกทิศทาง ให้เราดูว่าสเกลแฟกเตอร์เปลี่ยนแปลงไปอย่างไรตามเวลาในขั้นตอนต่อไปนี้
Step 1 - สำหรับจักรวาลแบบคงที่สเกลแฟคเตอร์คือ 1 นั่นคือค่าของระยะทางร่วมคือระยะห่างระหว่างวัตถุ
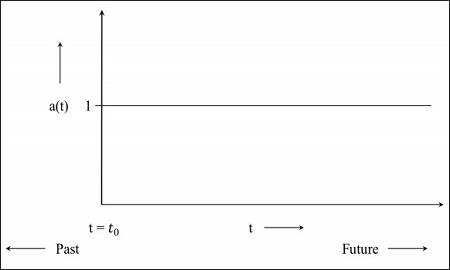
Step 2- ภาพต่อไปนี้เป็นกราฟของเอกภพที่ยังคงขยายตัว แต่มีอัตราที่ลดลงซึ่งหมายความว่ากราฟจะเริ่มต้นในอดีต t = 0 บ่งชี้ว่าจักรวาลเริ่มต้นจากจุดนั้น

Step 3 - ภาพต่อไปนี้เป็นกราฟของจักรวาลที่กำลังขยายตัวในอัตราที่เร็วขึ้น

Step 4 - ภาพต่อไปนี้เป็นกราฟสำหรับจักรวาลที่เริ่มหดตัวนับจากนี้

หากค่าของสเกลแฟคเตอร์กลายเป็น 0 ในระหว่างการหดตัวของจักรวาลมันแสดงถึงระยะห่างระหว่างวัตถุ 0กล่าวคือระยะทางที่เหมาะสมจะกลายเป็น 0. ระยะทางร่วมซึ่งเป็นระยะห่างระหว่างวัตถุในจักรวาลปัจจุบันเป็นปริมาณคงที่ ในอนาคตเมื่อสเกลแฟคเตอร์กลายเป็น0ทุกอย่างจะใกล้เข้ามามากขึ้น แบบจำลองขึ้นอยู่กับส่วนประกอบของจักรวาล
เมตริกสำหรับแบน (ยุคลิด: ไม่มีพารามิเตอร์สำหรับความโค้ง) ที่ขยายจักรวาลได้รับเป็น -
$$ ds ^ 2 = a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right) $$
สำหรับปริภูมิ - เวลาองค์ประกอบเส้นที่เราได้รับในสมการข้างต้นจะถูกแก้ไขเป็น -
$$ ds ^ 2 = c ^ 2dt ^ 2 - \ left \ {a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ ขวา) \ right \} $$
สำหรับพื้นที่ - เวลาเวลาที่โฟตอนถูกปล่อยออกมาและเมื่อตรวจพบจะแตกต่างกัน ระยะทางที่เหมาะสมคือระยะทางไปยังวัตถุในทันทีซึ่งสามารถเปลี่ยนแปลงได้ตลอดเวลาเนื่องจากการขยายตัวของจักรวาล เป็นระยะทางที่โฟตอนเดินทางจากวัตถุต่าง ๆ เพื่อมาหาเรา มันเกี่ยวข้องกับระยะ comoving เป็น -
$$ d_p = a (t) \ times d_c $$
โดยที่ $ d_p $ คือระยะทางที่เหมาะสมและ $ d_c $ คือระยะ comoving ซึ่งได้รับการแก้ไข
ระยะทางที่วัดกับวัตถุในจักรวาลปัจจุบันถือเป็นระยะทางร่วมซึ่งหมายความว่าระยะทางร่วมจะคงที่และไม่เปลี่ยนแปลงโดยการขยายตัว ในอดีตสเกลแฟคเตอร์มีค่าน้อยกว่า 1 ซึ่งบ่งชี้ว่าระยะทางที่เหมาะสมนั้นเล็กกว่า
เราสามารถวัดการเปลี่ยนสีแดงไปยังดาราจักรได้ ดังนั้นระยะทางที่เหมาะสม $ d_p $ จึงสอดคล้องกับ $ c \ times t (z) $ โดยที่ $ t (z) $ คือเวลามองย้อนกลับไปสู่การเปลี่ยนสีแดงและ c คือความเร็วของแสงในสุญญากาศ เวลามองย้อนกลับเป็นฟังก์ชันของการเปลี่ยนสีแดง(z).
จากแนวคิดข้างต้นให้เราวิเคราะห์ว่าการเปลี่ยนสีแดงของจักรวาลถูกตีความอย่างไรในสถานการณ์นี้ของ $ d_p = a (t) \ times d_c $
สมมติว่าโฟตอน (ซึ่งเป็นขอบเขตโลก) ถูกปล่อยออกมาจากกาแล็กซี่ G. $ t_ {em} $ ตรงกับเวลาที่โฟตอนถูกปล่อยออกมา $ a (t_ {em}) $ คือสเกลแฟคเตอร์ในขณะนั้นเมื่อโฟตอนถูกปล่อยออกมา เมื่อถึงเวลาตรวจจับโฟตอนจักรวาลทั้งหมดได้ขยายตัวกล่าวคือโฟตอนจะเปลี่ยนเป็นสีแดงเมื่อตรวจพบ $ t_ {obs} $ ตรงกับเวลาที่ตรวจพบโฟตอนและสเกลแฟกเตอร์ที่สอดคล้องกันคือ $ a (t_ {obs}) $
ปัจจัยที่จักรวาลเติบโตขึ้นนั้นได้รับจาก -
$$ \ frac {a (t_ {obs})} {a (t_ {em})} $$
ปัจจัยที่ทำให้ความยาวคลื่นขยายตัวคือ -
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
ซึ่งเท่ากับปัจจัยที่จักรวาลเติบโตขึ้น สัญลักษณ์มีความหมายตามปกติ ดังนั้น,
$$ \ frac {a (t_ {obs})} {a (t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
เรารู้ว่าการเปลี่ยนสีแดง (z) คือ -
$$ z = \ frac {\ lambda_ {obs} - \ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} - 1 $$
$$ 1 + z = \ frac {a (t_ {obs})} {a (t_ {em})} $$
มูลค่าปัจจุบันของสเกลแฟคเตอร์คือ 1 ดังนั้น $ a (t_ {obs}) = 1 $ และแสดงถึงสเกลแฟคเตอร์เมื่อโฟตอนถูกปล่อยออกมาในอดีตโดย $ a (t) $
ดังนั้น,
$$ 1 + z = \ frac {1} {a (t)} $$
การตีความ Redshift ในจักรวาลวิทยา
เพื่อให้เข้าใจสิ่งนี้ให้เราใช้ตัวอย่างต่อไปนี้: ถ้า $ z = 2 $ แล้ว $ a (t) = 1/3 $
โดยนัยว่าเอกภพได้ขยายตัวด้วยปัจจัยสามเนื่องจากแสงออกจากวัตถุนั้น ความยาวคลื่นของรังสีที่ได้รับมีการขยายตัวขึ้นเป็น 3 เท่าเนื่องจากพื้นที่ได้ขยายตัวโดยปัจจัยเดียวกันระหว่างการขนส่งจากวัตถุที่เปล่งออกมา ควรสังเกตว่าด้วยค่าที่มากเช่นนี้zการเปลี่ยนสีแดงส่วนใหญ่เป็นการเปลี่ยนสีแดงของจักรวาลและไม่ใช่การวัดความเร็วถอยที่แท้จริงของวัตถุที่เกี่ยวข้องกับเรา
สำหรับพื้นหลังไมโครเวฟจักรวาล (CMB) z = 1089ซึ่งหมายความว่าจักรวาลปัจจุบันได้ขยายตัวโดยปัจจัยของ ∼1090. ตัวชี้วัดสำหรับเอกภพแบนแบบยูคลิดและขยายได้รับเป็น -
$$ ds ^ 2 = a ^ 2 (t) (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2) $$
เราต้องการเขียนเมตริกในส่วนโค้งใด ๆ
Robertson and Walker ได้รับการพิสูจน์แล้วสำหรับเอกภพที่มีความโค้ง (ซึ่งเป็นเนื้อเดียวกันและเป็นไอโซทรอปิก) เมตริกจะได้รับเป็น -
$$ ds ^ 2 = a ^ 2 (t) \ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right] $$
โดยทั่วไปเรียกว่า Robertson–Walker Metricและเป็นจริงสำหรับโทโพโลยีของอวกาศ โปรดสังเกตปัจจัยพิเศษใน $ dr ^ 2 $ ที่นี่ คือค่าคงที่ความโค้ง
เรขาคณิตของจักรวาล
เรขาคณิตของจักรวาลอธิบายด้วยความช่วยเหลือของ Curvatures ต่อไปนี้ซึ่งรวมถึง -
- ความโค้งเชิงบวก
- ความโค้งเชิงลบ
- ความโค้งเป็นศูนย์
ให้เราเข้าใจรายละเอียดแต่ละข้อ
ความโค้งเชิงบวก
ถ้าระนาบแทนเจนต์ที่ลากมาที่จุดใด ๆ บนพื้นผิวของความโค้งไม่ตัดกันที่จุดใด ๆ บนพื้นผิวจะเรียกว่าพื้นผิวที่มีความโค้งเป็นบวกคือพื้นผิวอยู่ที่ด้านหนึ่งของระนาบสัมผัส ณ จุดนั้น พื้นผิวของทรงกลมมีความโค้งเป็นบวก
ความโค้งเชิงลบ
ถ้าระนาบสัมผัสที่ลากมาที่จุดหนึ่งบนพื้นผิวของความโค้งตัดกันที่จุดใด ๆ บนพื้นผิวจะเรียกว่าพื้นผิวที่มีความโค้งเป็นลบกล่าวคือพื้นผิวโค้งออกจากระนาบสัมผัสในสองทิศทางที่ต่างกัน พื้นผิวรูปอานมีความโค้งเชิงลบ
ตอนนี้พิจารณาพื้นผิวของทรงกลม ถ้าสามเหลี่ยมถูกสร้างขึ้นบนพื้นผิวของทรงกลมโดยการรวมจุดสามจุดด้วย geodesic (ส่วนโค้งของวงกลมใหญ่) ผลรวมของมุมภายในของสามเหลี่ยมทรงกลมจะมากกว่า 180 oนั่นคือ
$$ \ alpha + \ beta + \ gamma> \ pi $$
ช่องว่างดังกล่าวเรียกว่าช่องว่างโค้งบวก นอกจากนี้ความโค้งยังเป็นเนื้อเดียวกันและไอโซทรอปิก โดยทั่วไปมุมที่จุดยอดของสามเหลี่ยมทรงกลมจะเป็นไปตามความสัมพันธ์ -
$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$
ที่ไหน A คือพื้นที่ของสามเหลี่ยมและ Rคือรัศมีของทรงกลม ภาพต่อไปนี้แสดงให้เห็นถึงพื้นที่โค้งในเชิงบวก

สำหรับความโค้งที่เป็นบวกเส้นขนานควรจะบรรจบกัน พิจารณาพื้นผิวโลกซึ่งเป็นพื้นที่โค้งเป็นบวก ใช้จุดเริ่มต้นสองจุดบนเส้นศูนย์สูตร เส้นที่ข้ามเส้นศูนย์สูตรที่มุมฉากเรียกว่าเส้นลองจิจูด เนื่องจากเส้นเหล่านี้พาดผ่านเส้นศูนย์สูตรที่มุมฉากจึงเรียกได้ว่าเส้นขนาน เริ่มจากเส้นศูนย์สูตรในที่สุดพวกเขาก็ตัดกันที่ขั้ว วิธีนี้ถูกใช้โดยCarl Gauss และคนอื่น ๆ เพื่อทำความเข้าใจโทโพโลยีของโลก
พิจารณาพื้นที่โค้งเชิงลบ (อานที่แสดงในภาพต่อไปนี้) ผลรวมของมุมภายในของสามเหลี่ยมน้อยกว่า 180 oนั่นคือ -
$$ \ alpha + \ beta + \ gamma <\ pi $$
มุมที่จุดยอดเป็นไปตามความสัมพันธ์ -
$$ \ alpha + \ beta + \ gamma = \ pi - A / R ^ 2 $$

ความโค้งเป็นศูนย์
พื้นผิวระนาบมีความโค้งเป็นศูนย์ ตอนนี้สำหรับพื้นที่ราบถ้าเครื่องบินถูกนำมาและสร้างสามเหลี่ยมโดยการรวมจุดสามจุดด้วย geodesic (เส้นตรง) ผลรวมของมุมภายในจะเป็น -
$$ \ alpha + \ beta + \ gamma = \ pi $$
ภาพต่อไปนี้เป็นพื้นที่ 2 มิติแบบแบน

หากต้องการให้พื้นที่เป็นเนื้อเดียวกันและเป็นไอโซทรอปิกจะมีความเป็นไปได้เพียงสามประการเท่านั้น: พื้นที่สามารถแบนสม่ำเสมอหรืออาจมีความโค้งเชิงบวกสม่ำเสมอหรืออาจมีความโค้งเชิงลบที่สม่ำเสมอ
ค่าคงที่ความโค้งสามารถสันนิษฐานได้จากสามค่าต่อไปนี้
$$ k = \ start {cases} +1, & for \: a \: positively \: curve \: space; \\\ quad 0, & for \: a \: flat \: space; \\ - 1, & for \: a \: negatively \: โค้ง \: space; \ end {cases} $$
โทโพโลยีสากลของจักรวาล
เอกภพมีโทโพโลยีบางอย่าง แต่ในพื้นที่สามารถมีริ้วรอยได้ ขึ้นอยู่กับวิธีการกระจายของสสารในอวกาศความโค้งจะมีรูปแบบที่เล็กกว่า ให้เราสมมติว่ามีชั้นของวัตถุที่มีขนาดจริงเท่ากันไม่ว่าจะอยู่ที่ใดในจักรวาลซึ่งหมายความว่าพวกมันเหมือนเทียนมาตรฐาน มีความสว่างไม่เท่ากัน แต่มีขนาดเท่ากัน
ถ้าวัตถุอยู่ในพื้นที่โค้งเป็นบวกและโฟตอนมาจากจุด A (ปลายด้านหนึ่งของวัตถุ) และ B (ปลายอีกด้านหนึ่งของวัตถุ) โฟตอนจะแพร่กระจายขนานกันในอวกาศโค้งเชิงบวกผ่านเส้นทางของธรณีสัณฐานและในที่สุดก็จะมาบรรจบกัน . สำหรับผู้สังเกตที่ C จะดูเหมือนว่ามันมาจากสองจุดที่แตกต่างกันในทิศทางที่ต่างกัน
ถ้าวัตถุอยู่ในเอกภพเฉพาะที่และเราวัดขนาดเชิงมุมวัตถุนั้นจะไม่ได้รับผลกระทบจากความโค้ง หากวัตถุคลาสเดียวกันถูกมองเห็นด้วยการเปลี่ยนสีแดงที่มากขึ้นขนาดเชิงมุมจะไม่สัมพันธ์กับ
$$ \ theta = \ frac {d} {r} $$
ที่ไหน d คือขนาดของวัตถุและ rคือระยะทางไปยังวัตถุกล่าวคือถ้าขนาดมากกว่าขนาดท้องถิ่นหมายความว่าความโค้งเป็นบวก ภาพต่อไปนี้เป็นภาพแทนของโฟตอนที่ตรวจพบในพื้นที่โค้งเป็นบวก

เป็นที่น่าสังเกตว่าไม่มีวัตถุทางดาราศาสตร์ฟิสิกส์ที่มีขนาดและสัณฐานมาตรฐานจริง แม้ว่าจะมีการคิดว่าดาราจักรซีดี - รูปไข่ขนาดมหึมาจะพอดีกับแท่งเทียนมาตรฐาน แต่ก็พบว่ามีการพัฒนาไปตามกาลเวลาเช่นกัน
การค้นหาระยะทางไปยังกาแลคซี
ในส่วนนี้เราจะพูดถึงวิธีการหาระยะทางไปยังกาแลคซีโดยพิจารณาจากภาพต่อไปนี้

พิจารณาทางช้างเผือกที่ (r, θ,) ในกรอบพักของจักรวาล หนึ่งสามารถใช้ = 0; (0, θ, ϕ) คือศูนย์กลางของจักรวาลโดยเรียกใช้สมมติฐานของความเป็นเนื้อเดียวกัน
Consider a galaxy ‘G’ at (r1, θ,). The distance (proper) is the shortest radial distance travelled by a photon. From the symmetry of space – time, the null geodesic from r = 0 to r = r1, has a constant direction in space. In its radial propagation, the angular co-ordinates do not change. If angular co–ordinates get changed, then it is not the shortest path. That is the reason why the curvature term is present in dr2.
Points to Remember
The expansion of the universe is in all the directions.
The universe can be static, expanding or contracting depending upon the scale factor evolution.
The cD-galaxies evolve with time and hence cannot be used as standard candles.
The universe has certain topology, but locally it can have wrinkles.