จักรวาลวิทยา - วิธีการขนส่ง
วิธีการขนส่ง (Kepler Space Telescope)ใช้เพื่อหาขนาด การลดลงของความสว่างของดาวโดยดาวเคราะห์มักจะน้อยกว่าระบบเลขฐานสอง
F0 เป็นฟลักซ์ของดาวก่อนที่ดาวเคราะห์จะเกิด
F1 คือฟลักซ์หลังจากที่ดาวเคราะห์ทั้งดวงอยู่ตรงหน้าดาว
ภาพต่อไปนี้จะใช้สำหรับการคำนวณทั้งหมด

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$
$$ \ frac {\ Delta F} {F} \ Cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {earth} \ Cong 0.001 \% $$
$$ \ left (\ frac {\ Delta F} {F} \ right) _ {jupiter} \ Cong 1 \% $$
นี่ไม่ใช่เรื่องง่ายที่จะบรรลุได้ด้วยกล้องโทรทรรศน์ภาคพื้นดิน ทำได้โดยกล้องโทรทรรศน์ฮับเบิล

ที่นี่ $ t_T $ คือเวลาระหว่างตำแหน่ง A และ D และ $ t_F $ คือเวลาระหว่างตำแหน่ง B และ C
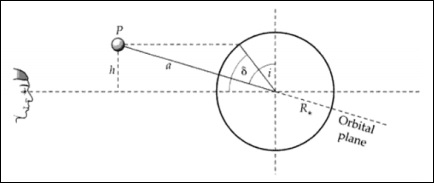
รูปทรงเรขาคณิตของการขนส่งที่เกี่ยวข้องกับความเอียง iของระบบ ละติจูดและความเอียงของการขนส่งสามารถใช้แทนกันได้
จากภาพด้านบนเราสามารถเขียน -
$$ \ frac {h} {a} = cos (i) $$
$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$
$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$
$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$
$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$
$$ sin (\ theta) = \ frac {y} {a} $$
$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$
$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$
ที่นี่ $ t_T $ คือเศษส่วนของช่วงเวลาที่การขนส่งเกิดขึ้นและ (2θ / 2π) เป็นเศษส่วนของมุมที่การขนส่งเกิดขึ้น
$$ บาป (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
โดยปกติ a >> R ∗ >> Rp. ดังนั้นเราสามารถเขียน -
$$ บาป (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ right] ^ {\ frac {1} {2}} $$
ที่นี่ Pคือระยะเวลาระหว่างการส่งสัญญาณสองครั้งต่อเนื่องกัน เวลาในการขนส่งน้อยมากเมื่อเทียบกับช่วงเวลาโคจร ดังนั้น
$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}} $$
ที่นี่ tT, P, R∗ เป็นสิ่งที่สังเกตได้ a และ i ควรจะค้นพบ
ตอนนี้
$$ บาป (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
โดยที่ $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $
ปล่อย,
$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2 $$
ตอนนี้เราสามารถแสดงออก
$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$
สำหรับดาวลำดับหลัก
$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$
$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$
สิ่งนี้ให้ R∗.
ดังนั้นเราจึงได้รับค่าของ 'a' ด้วย
ดังนั้นเราจึงได้ 'R p ', 'ap' และแม้แต่ 'i'
สำหรับทั้งหมดนี้
$$ h \ leq R_ \ ast + R_p $$
$$ a \: cos \: i \ leq R_ \ ast + R_p $$
แม้กระทั่ง ~ 89 องศาระยะเวลาการขนส่งจะน้อยมาก ดาวเคราะห์ต้องอยู่ใกล้มากเพื่อให้มีเวลาขนส่งเพียงพอ สิ่งนี้ทำให้เกิดข้อ จำกัด ที่เข้มงวดใน "i" เมื่อเราได้ 'i' เราจะได้ 'm p ′ จากการวัดความเร็วตามแนวรัศมี
การตรวจจับโดยวิธีขนส่งนี้เรียกว่าการตรวจจับโอกาสกล่าวคือความน่าจะเป็นของการสังเกตการขนส่ง การคำนวณความน่าจะเป็นของการขนส่ง (ความน่าจะเป็นของการสังเกต) แสดงไว้ด้านล่าง
ความน่าจะเป็นในการขนส่งนั้นสัมพันธ์กับมุมที่เป็นของแข็งที่ตรวจสอบได้โดยการกำหนดค่าการขนส่งที่รุนแรงสองแบบซึ่งก็คือ -
$$ Solid \: angle \: of \: planet \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right) $$
เช่นเดียวกับมุมของแข็งทั้งหมดที่แกนกึ่งหลัก a หรือ -
$$ Solid \: angle \: of \: sphere \: = \: 4 \ pi $$
ความน่าจะเป็นคืออัตราส่วนของพื้นที่ทั้งสองนี้ -
$$ = \: \ frac {area \: of \: sky \: covered \: by \: favorable \: orientation} {area \: of \: sky \: covered \: by \: all \: possible \: ปฐมนิเทศ \: of \: orbit} $$
$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \: of \: hollow \: cyclinder} {area \ : of \: sphere} $
ความน่าจะเป็นนี้ไม่ขึ้นอยู่กับผู้สังเกต
สิ่งที่ต้องจำ
- วิธีการขนส่ง (กล้องโทรทรรศน์อวกาศเคปเลอร์) ใช้เพื่อหาขนาด
- การตรวจจับโดยวิธีขนส่งเป็นการตรวจจับโอกาส
- ดาวเคราะห์ต้องอยู่ใกล้มากเพื่อให้มีเวลาขนส่งเพียงพอ
- ความน่าจะเป็นในการขนส่งเกี่ยวข้องกับมุมของแข็งของดาวเคราะห์
- ความน่าจะเป็นนี้ไม่ขึ้นอยู่กับกรอบอ้างอิงของผู้สังเกตการณ์