ทฤษฎีเครือข่าย - การแปลงเดลต้าเป็นดาว
ในบทที่แล้วเราได้กล่าวถึงปัญหาตัวอย่างที่เกี่ยวข้องกับความต้านทานที่เท่ากัน ที่นั่นเราคำนวณequivalent resistanceระหว่างขั้ว A & B ของเครือข่ายไฟฟ้าที่กำหนดได้อย่างง่ายดาย เนื่องจากในทุกขั้นตอนเรามีการรวมกันของตัวต้านทานที่เชื่อมต่อในรูปแบบอนุกรมหรือรูปแบบขนาน
อย่างไรก็ตามในบางสถานการณ์เป็นการยากที่จะลดความซับซ้อนของเครือข่ายโดยทำตามแนวทางก่อนหน้านี้ ตัวอย่างเช่นตัวต้านทานที่เชื่อมต่อในรูปแบบเดลต้า (δ) หรือรูปดาว ในสถานการณ์เช่นนี้เราต้องconvertเครือข่ายของรูปแบบหนึ่งไปยังอีกรูปแบบหนึ่งเพื่อให้ง่ายขึ้นโดยใช้ชุดค่าผสมหรือชุดค่าผสมแบบขนาน ในบทนี้ให้เราพูดคุยเกี่ยวกับไฟล์Delta to Star Conversion.
เครือข่ายเดลต้า
พิจารณาสิ่งต่อไปนี้ delta network ดังแสดงในรูปต่อไปนี้
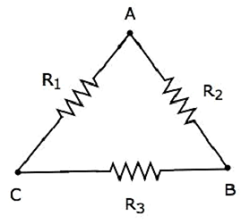
สมการต่อไปนี้แสดงถึง equivalent resistance ระหว่างสองขั้วของเครือข่ายเดลต้าเมื่อเทอร์มินัลที่สามเปิดอยู่
$$ R_ {AB} = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $$
$$ R_ {BC} = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $$
$$ R_ {CA} = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $$
เครือข่ายสตาร์
รูปต่อไปนี้แสดงไฟล์ equivalent star network สอดคล้องกับเครือข่ายเดลต้าข้างต้น
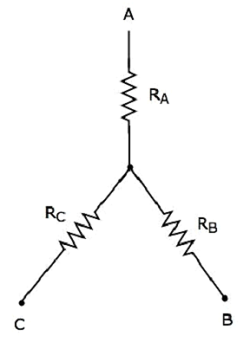
สมการต่อไปนี้แสดงถึง equivalent resistance ระหว่างสองขั้วของเครือข่ายดาวเมื่อขั้วที่สามเปิดอยู่
$$ R_ {AB} = R_A + R_B $$
$$ R_ {BC} = R_B + R_C $$
$$ R_ {CA} = R_C + R_A $$
ความต้านทานเครือข่ายดาวในแง่ของความต้านทานเครือข่ายเดลต้า
เราจะได้สมการต่อไปนี้โดยการหาเงื่อนไขด้านขวามือของสมการข้างต้นซึ่งเงื่อนไขด้านซ้ายมือจะเหมือนกัน
$ R_A + R_B = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B + R_C = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C + R_A = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $ Equation 3
โดยการเพิ่มสามสมการข้างต้นเราจะได้
$$ 2 (R_A + R_B + R_C) = \ frac {2 (R_1 R_2 + R_2 R_3 + R_3 R_1)} {R_1 + R_2 + R_3} $$
$ \ Rightarrow R_A + R_B + R_C = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} $ Equation 4
ลบสมการ 2 ออกจากสมการ 4
$ R_A + R_B + R_C - (R_B + R_C) = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} - \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $
$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$
โดยการลบสมการ 3 จากสมการ 4 เราจะได้
$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$
โดยการลบสมการ 1 จากสมการ 4 เราจะได้
$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$
โดยใช้ความสัมพันธ์ข้างต้นเราสามารถค้นหาความต้านทานของเครือข่ายดาวจากความต้านทานของเครือข่ายเดลต้า ด้วยวิธีนี้เราสามารถแปลงไฟล์delta network เป็น star network.
ตัวอย่าง
ให้เราคำนวณ resistances of star networkซึ่งเทียบเท่ากับเดลต้าเน็ตเวิร์กดังแสดงในรูปต่อไปนี้
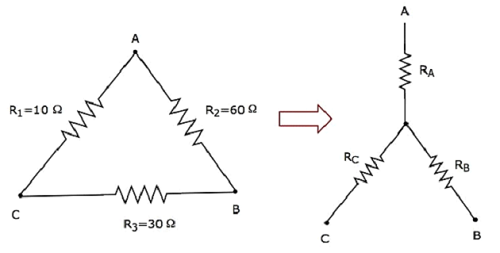
ได้รับ resistances of delta networkเป็นR 1 = 10 Ω, R 2 = 60 ΩและR 3 = 30 Ω
เราทราบความสัมพันธ์ดังต่อไปนี้ของความต้านทานของเครือข่ายดาวในแง่ของความต้านทานของเครือข่ายเดลต้า
$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$
$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$
$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$
แทนค่าของR 1 , R 2และR 3ในสมการข้างต้น
$$ R_A = \ frac {10 \ times 60} {10 + 60 + 30} = \ frac {600} {100} = 6 \ Omega $$
$$ R_B = \ frac {60 \ times 30} {10 + 60 + 30} = \ frac {1800} {100} = 18 \ Omega $$
$$ R_C = \ frac {30 \ times 10} {10 + 60 + 30} = \ frac {300} {100} = 3 \ Omega $$
ดังนั้นเราจึงได้ความต้านทานของเครือข่ายดาวเป็น RA = 6 Ω, RB = 18 Ω และ RC = 3 Ωซึ่งเทียบเท่ากับความต้านทานของเครือข่ายเดลต้าที่กำหนด