ทฤษฎีเครือข่าย - การตอบสนองของวงจรไฟฟ้ากระแสตรง

หากเอาต์พุตของวงจรไฟฟ้าสำหรับอินพุตแตกต่างกันไปตามเวลาจะเรียกว่าเป็น time response. การตอบสนองต่อเวลาประกอบด้วยสองส่วนต่อไปนี้

• การตอบสนองชั่วคราว
• การตอบสนองต่อสภาวะคงที่

ในบทนี้ก่อนอื่นให้เราพูดคุยเกี่ยวกับการตอบสนองทั้งสองนี้จากนั้นสังเกตการตอบสนองทั้งสองนี้ในวงจร RL แบบอนุกรมเมื่อมีการกระตุ้นด้วยแหล่งจ่ายแรงดันไฟฟ้ากระแสตรง

การตอบสนองชั่วคราว

หลังจากใช้อินพุตกับวงจรไฟฟ้าแล้วเอาต์พุตจะใช้เวลาพอสมควรในการเข้าสู่สภาวะคงที่ ดังนั้นเอาต์พุตจะอยู่ในสถานะชั่วคราวจนกว่าจะเข้าสู่สภาวะคงที่ ดังนั้นการตอบสนองของวงจรไฟฟ้าในสถานะชั่วคราวจึงเรียกว่าtransient response.

การตอบสนองชั่วคราวจะเป็นศูนย์สำหรับค่าขนาดใหญ่ของ 't' ตามหลักการแล้วค่า "t" นี้ควรเป็นอินฟินิตี้ แต่ในทางปฏิบัติfive time constants เพียงพอแล้ว

การมีอยู่หรือไม่มีชั่วคราว

ชั่วคราวเกิดขึ้นในการตอบสนองเนื่องจาก sudden changeในแหล่งที่มาที่ใช้กับวงจรไฟฟ้าและ / หรือเนื่องจากการสลับการกระทำ มีสองการดำเนินการสลับที่เป็นไปได้ สิ่งเหล่านี้คือสวิตช์เปิดและสวิตช์ปิด

• transient ส่วนจะ not presentในการตอบสนองของวงจรไฟฟ้าหรือเครือข่ายหากมีเพียงความต้านทาน เพราะresistor มีความสามารถในการปรับแรงดันและกระแสไฟฟ้าจำนวนเท่าใดก็ได้

• transient part occurs ในการตอบสนองของวงจรไฟฟ้าหรือเครือข่ายเนื่องจากมีองค์ประกอบกักเก็บพลังงานเช่น inductor and capacitor. เนื่องจากไม่สามารถเปลี่ยนพลังงานที่เก็บไว้ในองค์ประกอบเหล่านั้นได้ทันที

พฤติกรรมตัวเหนี่ยวนำ

สมมติว่าการดำเนินการสลับเกิดขึ้นที่t = 0Inductor currentไม่เปลี่ยนแปลงทันทีเมื่อมีการดำเนินการสลับ นั่นหมายความว่าค่าของกระแสไฟฟ้าเหนี่ยวนำหลังจากการดำเนินการสวิตชิ่งจะเหมือนกับค่าก่อนการดำเนินการสวิตชิ่ง

ในทางคณิตศาสตร์สามารถแสดงเป็น

$$ i_L (0 ^ +) = i_L (0 ^ -) $$

พฤติกรรมของตัวเก็บประจุ

capacitor voltageไม่เปลี่ยนทันทีคล้ายกับกระแสตัวเหนี่ยวนำเมื่อมีการดำเนินการสลับเกิดขึ้น นั่นหมายความว่าค่าของแรงดันไฟฟ้าของตัวเก็บประจุหลังจากการดำเนินการสวิตชิ่งจะเหมือนกับค่าก่อนการดำเนินการสวิตชิ่ง

ในทางคณิตศาสตร์สามารถแสดงเป็น

$$ v_c (0 ^ +) = v_c (0 ^ -) $$

การตอบสนองต่อสภาวะคงที่

ส่วนของการตอบสนองต่อเวลาที่ยังคงอยู่แม้ว่าการตอบสนองชั่วคราวจะกลายเป็นค่าศูนย์สำหรับค่าขนาดใหญ่ของ 't' เรียกว่า steady state response. ซึ่งหมายความว่าจะไม่มีส่วนใด ๆ ในการตอบสนองระหว่างสภาวะคงที่

พฤติกรรมตัวเหนี่ยวนำ

หากแหล่งจ่ายอิสระเชื่อมต่อกับวงจรไฟฟ้าหรือเครือข่ายที่มีตัวเหนี่ยวนำและตัวต้านทานอย่างน้อยหนึ่งตัว (อุปกรณ์เสริม) เป็นเวลานานแสดงว่าวงจรไฟฟ้าหรือเครือข่ายนั้นอยู่ในสถานะคงที่ ดังนั้นพลังงานที่เก็บไว้ในตัวเหนี่ยวนำของวงจรไฟฟ้านั้นจึงมีค่าสูงสุดและคงที่

ในทางคณิตศาสตร์สามารถแสดงเป็น

$ W_L = \ frac {L {i_L} ^ 2} {2} = $ สูงสุด & ค่าคงที่

$ \ Rightarrow i_L = $ สูงสุด & คงที่

ดังนั้นตัวเหนี่ยวนำจึงทำหน้าที่เป็น constant current source อยู่ในสถานะคงที่

แรงดันไฟฟ้าคร่อมตัวเหนี่ยวนำจะเป็น

$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$

ดังนั้นตัวเหนี่ยวนำจึงทำหน้าที่เป็น short circuit อยู่ในสถานะคงที่

พฤติกรรมของตัวเก็บประจุ

หากแหล่งจ่ายอิสระเชื่อมต่อกับวงจรไฟฟ้าหรือเครือข่ายที่มีตัวเก็บประจุและตัวต้านทานหนึ่งตัวหรือมากกว่า (อุปกรณ์เสริม) เป็นเวลานานแสดงว่าวงจรไฟฟ้าหรือเครือข่ายนั้นอยู่ในสถานะคงที่ ดังนั้นพลังงานที่เก็บไว้ในตัวเก็บประจุของวงจรไฟฟ้านั้นจึงมีค่าสูงสุดและคงที่

ในทางคณิตศาสตร์สามารถแสดงเป็น

$ W_c = \ frac {C {v_c} ^ 2} {2} = $ สูงสุด & ค่าคงที่

$ \ Rightarrow v_c = $ สูงสุด & คงที่

ดังนั้นตัวเก็บประจุทำหน้าที่เป็น constant voltage source อยู่ในสถานะคงที่

กระแสที่ไหลผ่านตัวเก็บประจุจะเป็น

$$ i_c = C \ frac {dv_c} {dt} = 0A $$

ดังนั้นตัวเก็บประจุจึงทำหน้าที่เป็น open circuit อยู่ในสถานะคงที่

การค้นหาการตอบสนองของวงจร Series RL

พิจารณาสิ่งต่อไปนี้ series RL circuit แผนภาพ

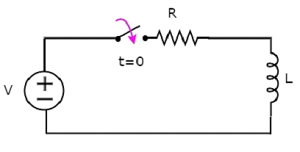
ในวงจรข้างต้นไฟล์ switch ถูกเก็บไว้ openสูงถึง t = 0 และปิดที่ t = 0 ดังนั้นแหล่งจ่ายแรงดันไฟฟ้ากระแสตรงที่มีโวลต์โวลต์จะไม่เชื่อมต่อกับวงจรซีรีส์ RL จนถึงช่วงเวลานี้ ดังนั้นจึงมีno initial current ไหลผ่านตัวเหนี่ยวนำ

แผนภาพวงจรเมื่อ switch อยู่ใน closed ตำแหน่งจะแสดงในรูปต่อไปนี้

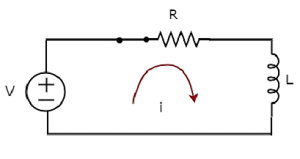
ตอนนี้กระแส i ไหลในวงจรทั้งหมดเนื่องจากแหล่งจ่ายแรงดันไฟฟ้ากระแสตรงมี V โวลต์เชื่อมต่อกับวงจรซีรีส์ RL

ตอนนี้สมัคร KVL รอบวง

$$ V = Ri + L \ frac {di} {dt} $$

$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1

สมการข้างต้นเป็นสมการเชิงอนุพันธ์ลำดับที่หนึ่งและอยู่ในรูปของ

$ \ frac {dy} {dt} + Py = Q $Equation 2

โดย comparing สมการ 1 และสมการ 2 เราจะได้ความสัมพันธ์ดังต่อไปนี้

$$ x = t $$

$$ y = i $$

$$ P = \ frac {R} {L} $$

$$ Q = \ frac {V} {L} $$

solution ของสมการ 2 จะเป็น

$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3

ที่ไหน k คือค่าคงที่

แทนค่าของ x, y, P & Q ในสมการ 3

$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $

$ \ Rightarrow เช่น ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $

$ \ Rightarrow เช่น ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $

$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4

เรารู้ว่าไม่มีกระแสไฟฟ้าเริ่มต้นในวงจร ดังนั้นแทนที่t = 0 และ = 0 ในสมการ 4 เพื่อหาค่าของค่าคงที่ k.

$$ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $$

$$ 0 = \ frac {V} {R} + k (1) $$

$$ k = - \ frac {V} {R} $$

แทนค่าของ k ในสมการ 4

$$ i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$

$$ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$

ดังนั้นไฟล์ current ไหลผ่านวงจรคือ

$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5

ดังนั้นการตอบสนองของวงจรซีรีส์ RL เมื่อมันถูกกระตุ้นด้วยแหล่งจ่ายแรงดันไฟฟ้ากระแสตรงจึงมีสองคำต่อไปนี้

• คำแรก $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ สอดคล้องกับ transient response.

• คำที่สอง $ \ frac {V} {R} $ สอดคล้องกับ steady state response. คำตอบทั้งสองนี้แสดงในรูปต่อไปนี้

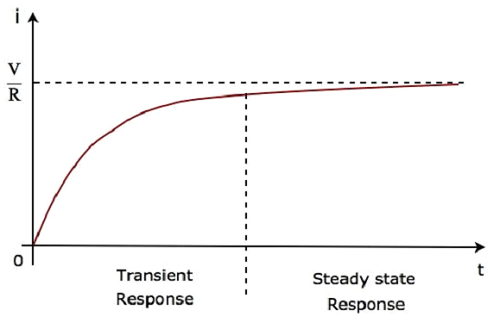
เราสามารถเขียนสมการ 5 ใหม่ได้ดังนี้ -

$ i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $

$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6

ที่ไหน τ คือ time constant และมูลค่าเท่ากับ $ \ frac {L} {R} $

ทั้งสมการ 5 และสมการ 6 เหมือนกัน แต่เราสามารถเข้าใจรูปคลื่นข้างต้นของกระแสที่ไหลผ่านวงจรจากสมการที่ 6 โดยการแทนที่ค่าสองสามค่าของt เช่น 0, τ, 2τ, 5τเป็นต้น

ในรูปคลื่นข้างต้นของกระแสที่ไหลผ่านวงจรการตอบสนองชั่วคราวจะแสดงค่าคงที่ของเวลาสูงสุดห้าค่าจากศูนย์ในขณะที่การตอบสนองสถานะคงที่จะแสดงตั้งแต่ค่าคงที่ห้าเวลาเป็นต้นไป