ทฤษฎีเครือข่าย - การตอบสนองของวงจรไฟฟ้ากระแสสลับ

ในบทที่แล้วเราได้กล่าวถึงการตอบสนองชั่วคราวและการตอบสนองต่อสภาวะคงที่ของวงจร DC ในบทนี้ให้เราพูดถึงไฟล์response of AC circuit. แนวคิดของการตอบสนองชั่วคราวและการตอบสนองต่อสภาวะคงที่ซึ่งเราได้กล่าวถึงในบทก่อนหน้านี้จะมีประโยชน์เช่นกัน

การค้นหาการตอบสนองของวงจร Series RL

พิจารณาสิ่งต่อไปนี้ series RL circuit แผนภาพ

ในวงจรข้างต้นไฟล์ switch ถูกเก็บไว้ openถึงt = 0และมันก็ปิดที่t = 0 ดังนั้นแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับที่มีแรงดันไฟฟ้าสูงสุดV _mโวลต์จึงไม่ได้เชื่อมต่อกับวงจรซีรีส์ RL จนถึงปัจจุบันนี้ ดังนั้นจึงมีno initial current ไหลผ่านตัวเหนี่ยวนำ

แผนภาพวงจรเมื่อ switch อยู่ใน closed ตำแหน่งดังแสดงในรูปต่อไปนี้

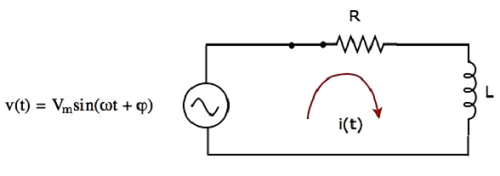
ตอนนี้กระแสi (t)ไหลในวงจรทั้งหมดเนื่องจากแหล่งจ่ายแรงดันไฟฟ้ากระแสสลับที่มีแรงดันไฟฟ้าสูงสุดV _mโวลต์เชื่อมต่อกับวงจรซีรีส์ RL

เรารู้ว่ากระแสi (t) ที่ไหลผ่านวงจรข้างต้นจะมีสองพจน์คำหนึ่งที่แสดงถึงส่วนชั่วคราวและคำอื่น ๆ แสดงถึงสถานะคงที่

ในทางคณิตศาสตร์สามารถแสดงเป็น

$ i (t) = i_ {Tr} (t) + i_ {ss} (t) $Equation 1

ที่ไหน

• $ i_ {Tr} (t) $ คือการตอบสนองชั่วคราวของกระแสที่ไหลผ่านวงจร

• $ i_ {ss} (t) $ คือการตอบสนองสภาวะคงที่ของกระแสที่ไหลผ่านวงจร

ในบทที่แล้วเราได้รับการตอบสนองชั่วคราวของกระแสที่ไหลผ่านวงจรซีรีส์ RL อยู่ในรูปแบบของ $ Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $

แทน $ i_ {Tr} (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $ ในสมการ 1

$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + i_ {ss} (t) $Equation 2

การคำนวณสถานะคงที่ในปัจจุบัน

หากสัญญาณไซน์ถูกนำไปใช้เป็นอินพุตให้กับวงจรไฟฟ้าเชิงเส้นมันจะสร้างเอาต์พุตที่คงที่ซึ่งก็คือ sinusoidal signal. ทั้งสัญญาณไซน์อินพุทและเอาท์พุทจะมีความถี่เท่ากัน แต่แอมพลิจูดและมุมเฟสต่างกัน

เราสามารถคำนวณการตอบสนองสภาวะคงที่ของวงจรไฟฟ้าเมื่อมันถูกกระตุ้นด้วยแหล่งจ่ายแรงดันไฟฟ้าแบบไซน์โดยใช้ Laplace Transform approach.

แผนภาพวงจร s-domain เมื่อ switch อยู่ใน closed ตำแหน่งดังแสดงในรูปต่อไปนี้

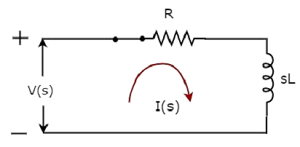
ในวงจรข้างต้นปริมาณและพารามิเตอร์ทั้งหมดจะแสดงเป็น s-domain. นี่คือการแปลง Laplace ของปริมาณและพารามิเตอร์โดเมนเวลา

Transfer function ของวงจรข้างต้นคือ

$$ H (s) = \ frac {I (s)} {V (s)} $$

$$ \ Rightarrow H (s) = \ frac {1} {Z (s)} $$

$$ \ Rightarrow H (s) = \ frac {1} {R + sL} $$

แทนที่ $ s = j \ omega $ ในสมการด้านบน

$$ H (j \ omega) = \ frac {1} {R + j \ omega L} $$

Magnitude of $ \ mathbf {\ mathit {H (j \ omega)}} $ คือ

$$ | H (j \ omega) | = \ frac {1} {\ sqrt {R ^ 2 + {\ omega} ^ 2} L ^ 2} $$

Phase angle of $ \ mathbf {\ mathit {H (j \ omega)}} $ คือ

$$ \ angle H (j \ omega) = -tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup $$

เราจะได้รับไฟล์ steady state current $ i_ {ss} (t) $ โดยทำสองขั้นตอนต่อไปนี้ -

• คูณแรงดันไฟฟ้าสูงสุดของแรงดันไฟฟ้าไซน์อินพุทและขนาดของ $ H (j \ omega) $

• เพิ่มมุมเฟสของแรงดันไฟฟ้าไซน์อินพุทและ $ H (j \ omega) $

steady state current $ i_ {ss} (t) $ จะเป็น

$$ i_ {ss} (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

แทนค่าของ $ i_ {ss} (t) $ ในสมการ 2

$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} บาป \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 3

เรารู้ว่าไม่มีกระแสไฟฟ้าเริ่มต้นในวงจร ดังนั้นแทนที่t = 0 & i (t) = 0ในสมการ 3 เพื่อหาค่าของค่าคงที่ K

$$ 0 = Ke ^ {- \ lgroup \ frac {0} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ โอเมก้า (0) + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

$$ \ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ โอเมก้า L} {R} \ rgroup \ rgroup $$

$$ \ Rightarrow K = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

แทนค่าของKในสมการ 3

$ i (t) = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2 }} sin \ lgroup \ โอเมก้า t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 4

สมการที่ 4 แสดงถึงกระแสที่ไหลผ่านวงจรอนุกรม RL เมื่อมันถูกกระตุ้นด้วยแหล่งกำเนิดแรงดันไฟฟ้ารูปไซน์ มันมีสองเทอม คำศัพท์ที่หนึ่งและสองแสดงถึงการตอบสนองชั่วคราวและการตอบสนองต่อสภาวะคงที่ของกระแสตามลำดับ

เราทำได้ neglect the first termของสมการ 4 เนื่องจากค่าของมันจะน้อยกว่าหนึ่งมาก ดังนั้นกระแสผลลัพธ์ที่ไหลผ่านวงจรจะเป็น

$$ i (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$

มันมีเฉพาะไฟล์ steady state term. ดังนั้นเราจึงพบได้เฉพาะการตอบสนองต่อสภาวะคงที่ของวงจรไฟฟ้ากระแสสลับและละเลยการตอบสนองชั่วคราวของมัน