ทฤษฎีเครือข่าย - เรโซแนนซ์แบบขนาน
ในบทที่แล้วเราได้กล่าวถึงความสำคัญของการสั่นพ้องแบบอนุกรม ตอนนี้ให้เราคุยเรื่องการสั่นพ้องแบบขนานในวงจร RLC
แผนภาพวงจรเรโซแนนซ์แบบขนาน
หากการสั่นพ้องเกิดขึ้นในวงจร RLC แบบขนานจะเรียกว่า as Parallel Resonance. พิจารณาสิ่งต่อไปนี้parallel RLC circuitซึ่งแสดงในโดเมนเฟสเซอร์
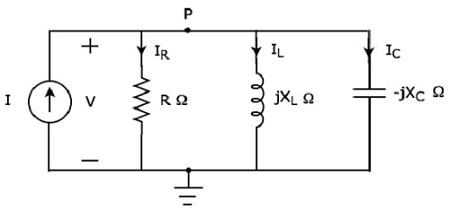
ที่นี่องค์ประกอบแบบพาสซีฟเช่นตัวต้านทานตัวเหนี่ยวนำและตัวเก็บประจุจะเชื่อมต่อแบบขนาน ชุดค่าผสมทั้งหมดนี้อยู่ในparallel ด้วยแหล่งที่มาของกระแสไซน์อินพุท
เขียน nodal equation ที่โหนดพี
$$ - I + I_R + I_L + I_C = 0 $$
$$ \ Rightarrow - I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0 $$
$$ \ Rightarrow I = \ frac {V} {R} - \ frac {jV} {X_L} + \ frac {jV} {X_C} $$
$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup] $Equation 1
สมการข้างต้นอยู่ในรูปของ I = VY.
ดังนั้นไฟล์ admittance Y ของวงจร RLC แบบขนานจะเป็น
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
พารามิเตอร์และปริมาณไฟฟ้าที่เรโซแนนซ์
ตอนนี้ให้เราหาค่าของพารามิเตอร์และปริมาณทางไฟฟ้าด้วยการสั่นพ้องของวงจร RLC แบบขนานทีละตัว
ความถี่เรโซแนนซ์
เรารู้ว่า resonant frequency, frคือความถี่ที่เกิดการสั่นพ้อง ในวงจรเรโซแนนซ์วงจร RLC แบบขนานเกิดขึ้นเมื่อระยะจินตภาพของการอนุญาติ Y เป็นศูนย์ กล่าวคือค่าของ $ \ frac {1} {X_C} - \ frac {1} {X_L} $ ควรจะเท่ากับศูนย์
$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$
$$ \ Rightarrow X_L = X_C $$
สภาพเรโซแนนซ์ข้างต้นเหมือนกับของวงจรซีรีส์ RLC ดังนั้นresonant frequency, fr จะเหมือนกันในวงจร RLC ทั้งสองชุดและวงจร RLC แบบขนาน
ดังนั้นไฟล์ resonant frequency, fr ของวงจร RLC แบบขนานคือ
$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$
ที่ไหน
- L คือความเหนี่ยวนำของตัวเหนี่ยวนำ
- C คือความจุของตัวเก็บประจุ
resonant frequency, fr ของวงจร RLC แบบขนานขึ้นอยู่กับความเหนี่ยวนำเท่านั้น L และความจุ C. แต่เป็นอิสระจากการต่อต้านR.
การรับเข้า
เราได้ไฟล์ admittance Y ของวงจร RLC แบบขนานเป็น
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
แทนที่ $ X_L = X_C $ ในสมการด้านบน
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_C} \ rgroup $$
$$ \ Rightarrow Y = \ frac {1} {R} + j (0) $$
$$ \ Rightarrow Y = \ frac {1} {R} $$
ที่เสียงสะท้อน admittance, Y ของวงจร RLC แบบขนานมีค่าเท่ากับความต้านทานซึ่งกันและกัน R คือ $ \ mathbf {\ mathit {Y = \ frac {1} {R}}} $
แรงดันไฟฟ้าในแต่ละองค์ประกอบ
แทน $ \ frac {1} {X_C} - \ frac {1} {X_L} = 0 $ ในสมการ 1
$$ I = V [\ frac {1} {R} + j (0)] $$
$$ \ Rightarrow I = \ frac {V} {R} $$
$$ \ Rightarrow V = IR $$
ดังนั้นไฟล์ voltage ในทุกองค์ประกอบของวงจร RLC แบบขนานที่เรโซแนนซ์คือ V = IR.
ที่การสั่นพ้องการยอมรับของวงจร RLC แบบขนานจะถึงค่าต่ำสุด ดังนั้นmaximum voltage มีอยู่ในแต่ละองค์ประกอบของวงจรนี้ที่เรโซแนนซ์
กระแสที่ไหลผ่านตัวต้านทาน
กระแสที่ไหลผ่านตัวต้านทานคือ
$$ I_R = \ frac {V} {R} $$
แทนค่าของ V ในสมการข้างต้น
$$ I_R = \ frac {IR} {R} $$
$$ \ Rightarrow I_R = I $$
ดังนั้นไฟล์ current flowing through resistor ที่ resonance คือ $ \ mathbf {\ mathit {I_R = I}} $
กระแสที่ไหลผ่านตัวเหนี่ยวนำ
กระแสที่ไหลผ่านตัวเหนี่ยวนำคือ
$$ I_L = \ frac {V} {j X_L} $$
แทนค่าของ V ในสมการข้างต้น
$$ I_L = \ frac {IR} {j X_L} $$
$$ \ Rightarrow I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I $$
$$ \ Rightarrow I_L = -jQI $$
ดังนั้นไฟล์ current flowing through inductor ที่เสียงสะท้อนคือ $ I_L = -jQI $
ดังนั้น magnitude ของกระแสที่ไหลผ่านตัวเหนี่ยวนำที่เรโซแนนซ์จะเป็น
$$ | I_L | = QI $$
โดยที่ Q คือ Quality factor และมูลค่าเท่ากับ $ \ frac {R} {X_L} $
กระแสที่ไหลผ่าน Capacitor
กระแสที่ไหลผ่านตัวเก็บประจุคือ
$$ I_C = \ frac {V} {- j X_C} $$
แทนค่าของ V ในสมการข้างต้น
$$ I_C = \ frac {IR} {- j X_C} $$
$$ \ Rightarrow I_C = j \ lgroup \ frac {R} {X_C} \ rgroup I $$
$$ \ Rightarrow I_C = jQI $$
ดังนั้นไฟล์ current flowing through capacitor ที่เสียงสะท้อนคือ $ I_C = jQI $
ดังนั้น magnitude ของกระแสที่ไหลผ่านตัวเก็บประจุที่เรโซแนนซ์จะเป็น
$$ | I_C | = QI $$
โดยที่ Q คือ Quality factor และมูลค่าเท่ากับ $ \ frac {R} {X_C} $
Note - วงจร RLC เรโซแนนซ์ขนานเรียกว่าเป็น current magnificationวงจร. เพราะขนาดของกระแสไฟฟ้าที่ไหลผ่านตัวเหนี่ยวนำและตัวเก็บประจุเท่ากับQครั้งอินพุตไซน์ปัจจุบันฉัน