หลักการหารปริมาณไฟฟ้า
ในบทนี้ให้เราพูดคุยเกี่ยวกับหลักการหารปริมาณไฟฟ้าสองข้อต่อไปนี้
- หลักการหารปัจจุบัน
- หลักการหารแรงดัน
หลักการหารปัจจุบัน
เมื่อมีการเชื่อมต่อองค์ประกอบแบบพาสซีฟสององค์ประกอบขึ้นไปแบบขนานปริมาณของกระแสไฟฟ้าที่ไหลผ่านแต่ละองค์ประกอบจะได้รับ divided (แชร์) กันเองจากกระแสที่เข้าสู่โหนด
พิจารณาสิ่งต่อไปนี้ circuit diagram.
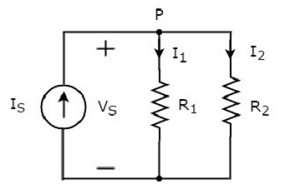
แผนภาพวงจรข้างต้นประกอบด้วยแหล่งกระแสอินพุต IS ขนานกับตัวต้านทานสองตัว R1 และ R2. แรงดันไฟฟ้าของแต่ละองค์ประกอบคือVS. กระแสที่ไหลผ่านตัวต้านทานR1 และ R2 คือ I1 และ I2 ตามลำดับ
KCL equation ที่โหนด P จะ
$$ I_S = I_1 + I_2 $$
แทนที่ $ I_1 = \ frac {V_S} {R_1} $ และ $ I_2 = \ frac {V_S} {R_2} $ ในสมการด้านบน
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} = V_S \ lgroup \ frac {R_2 + R_1} {R_1 R_2} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ lgroup \ frac {R_1R_2} {R_1 + R_2} \ rgroup $$
แทนค่าของV Sใน $ I_1 = \ frac {V_S} {R_1} $
$$ I_1 = \ frac {I_S} {R_1} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_1 = I_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
แทนค่าของV Sใน $ I_2 = \ frac {V_S} {R_2} $
$$ I_2 = \ frac {I_S} {R_2} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
จากสมการของI 1และI 2เราสามารถสรุปได้ว่ากระแสที่ไหลผ่านองค์ประกอบแฝงใด ๆ สามารถพบได้โดยใช้สูตรต่อไปนี้
$$ I_N = I_S \ lgroup \ frac {Z_1 \ rVert Z_2 \ rVert ... \ rVert Z_ {N-1}} {Z_1 + Z_2 + ... + Z_N} \ rgroup $$
นี้เรียกว่า current division principle และสามารถใช้ได้เมื่อสององค์ประกอบหรือมากกว่านั้นเชื่อมต่อแบบขนานและมีเพียงกระแสเดียวเท่านั้นที่เข้าสู่โหนด
ที่ไหน
ฉันยังไม่มีข้อความที่เป็นปัจจุบันที่ไหลผ่านองค์ประกอบ passive ของ N THสาขา
I Sคือกระแสอินพุตซึ่งเข้าสู่โหนด
Z 1 , Z 2 , ... , Z Nมีความต้านทาน 1 เซนต์สาขา 2 ครั้งสาขา, ... , N THสาขาตามลำดับ
หลักการหารแรงดัน
เมื่อมีการเชื่อมต่อองค์ประกอบแบบพาสซีฟสององค์ประกอบขึ้นไปเป็นอนุกรมปริมาณของแรงดันไฟฟ้าที่ปรากฏในแต่ละองค์ประกอบจะได้ divided (ใช้ร่วมกัน) จากแรงดันไฟฟ้าที่มีอยู่ในชุดค่าผสมทั้งหมดนั้น
พิจารณาสิ่งต่อไปนี้ circuit diagram.
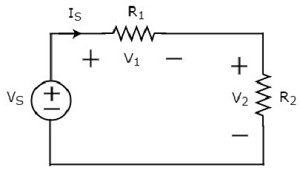
แผนภาพวงจรข้างต้นประกอบด้วยแหล่งจ่ายแรงดันที่ V Sในชุดที่มีสองตัวต้านทาน R 1และ R 2 ปัจจุบันที่ไหลผ่านองค์ประกอบเหล่านี้คือผมS แรงดันตกคร่อมตัวต้านทาน R 1และ R 2คือ V 1และ V 2ตามลำดับ
KVL equation รอบวงจะเป็น
$$ V_S = V_1 + V_2 $$
แทนV 1 = I S R 1และV 2 = I S R 2ในสมการข้างต้น
$$ V_S = I_S R_1 + I_S R_2 = I_S (R_1 + R_2) $$
$$ I_S = \ frac {V_S} {R_1 + R_2} $$
แทนค่าของฉันSในV 1 = ฉันS R 1
$$ V_1 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_1 $$
$$ \ Rightarrow V_1 = V_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
แทนค่าของฉันSในV 2 = ฉันS R 2
$$ V_2 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_2 $$
$$ \ Rightarrow V_2 = V_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
จากสมการของV 1และV 2เราสามารถสรุปได้ว่าแรงดันไฟฟ้าขององค์ประกอบแฝงใด ๆ สามารถพบได้โดยใช้สูตรต่อไปนี้
$$ V_N = V_S \ lgroup \ frac {Z_N} {Z_1 + Z_2 + .... + Z_N} \ rgroup $$
นี้เรียกว่า voltage division principle และสามารถใช้ได้เมื่อมีการเชื่อมต่อองค์ประกอบแบบพาสซีฟตั้งแต่สองชิ้นขึ้นไปเป็นอนุกรมและมีแรงดันไฟฟ้าเพียงตัวเดียวที่ใช้ได้ในชุดค่าผสมทั้งหมด
ที่ไหน
V Nคือแรงดันไฟฟ้าขององค์ประกอบพาสซีฟN th
V Sคือแรงดันไฟฟ้าขาเข้าซึ่งมีอยู่ตลอดทั้งชุดองค์ประกอบแบบพาสซีฟ
Z 1 , Z 2 , …, Z 3คืออิมพีแดนซ์ของ 1 st passive element, 2 nd passive element, …, N th passive element ตามลำดับ