ทฤษฎีเครือข่าย - เครือข่ายสองพอร์ต
โดยทั่วไปแล้วการวิเคราะห์เครือข่ายไฟฟ้าใด ๆ เป็นเรื่องง่ายหากแสดงด้วยแบบจำลองที่เทียบเท่าซึ่งให้ความสัมพันธ์ระหว่างตัวแปรอินพุตและเอาต์พุต สำหรับสิ่งนี้เราสามารถใช้two port networkการเป็นตัวแทน ตามชื่อที่แนะนำเครือข่ายสองพอร์ตประกอบด้วยสองพอร์ต พอร์ตหนึ่งใช้เป็นพอร์ตอินพุตและอีกพอร์ตหนึ่งใช้เป็นพอร์ตเอาต์พุต พอร์ตแรกและพอร์ตที่สองเรียกว่าพอร์ต 1 และพอร์ต 2 ตามลำดับ
One port networkเป็นเครือข่ายไฟฟ้าสองขั้วซึ่งกระแสจะไหลผ่านขั้วหนึ่งและออกจากขั้วอื่น ตัวต้านทานตัวเหนี่ยวนำและตัวเก็บประจุเป็นตัวอย่างของเครือข่ายพอร์ตหนึ่งเนื่องจากแต่ละตัวมีขั้วสองขั้ว การแสดงเครือข่ายพอร์ตหนึ่งพอร์ตจะแสดงในรูปต่อไปนี้
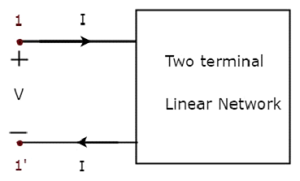
ที่นี่คู่ของเทอร์มินัล 1 & 1 'แสดงถึงพอร์ต ในกรณีนี้เรามีเพียงพอร์ตเดียวเนื่องจากเป็นเครือข่ายพอร์ตเดียว
ในทำนองเดียวกัน two port networkคือคู่ของเครือข่ายไฟฟ้าสองขั้วซึ่งกระแสจะไหลผ่านขั้วหนึ่งและออกจากขั้วอื่นของแต่ละพอร์ต การแสดงเครือข่ายพอร์ตสองพอร์ตจะแสดงในรูปต่อไปนี้
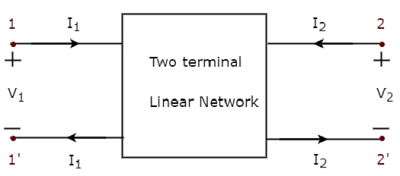
ในที่นี้เทอร์มินัลหนึ่งคู่ 1 & 1 'แทนพอร์ตหนึ่งพอร์ตซึ่งเรียกว่า port1 และอีกคู่ของเทอร์มินัล 2 & 2 'หมายถึงพอร์ตอื่นซึ่งเรียกว่าเป็น port2.
มี four variablesV 1 , V 2 , I 1และ I 2ในเครือข่ายสองพอร์ตดังแสดงในรูป จากนั้นเราสามารถเลือกตัวแปรสองตัวเป็นอิสระและอีกสองตัวแปรตาม เราจะได้สมการที่เป็นไปได้หกคู่ สมการเหล่านี้แสดงถึงตัวแปรตามในรูปของตัวแปรอิสระ ค่าสัมประสิทธิ์ของตัวแปรอิสระเรียกว่าparameters. ดังนั้นสมการแต่ละคู่จะให้พารามิเตอร์สี่ชุด
พารามิเตอร์เครือข่ายสองพอร์ต
พารามิเตอร์ของเครือข่ายสองพอร์ตถูกเรียกว่า two port network parametersหรือเพียงแค่พารามิเตอร์สองพอร์ต ต่อไปนี้เป็นประเภทของพารามิเตอร์เครือข่ายพอร์ตสองพอร์ต
- พารามิเตอร์ Z
- พารามิเตอร์ Y
- T พารามิเตอร์
- T 'พารามิเตอร์
- h-parameters
- g-parameters
ตอนนี้ให้เราพูดคุยเกี่ยวกับพารามิเตอร์เครือข่ายพอร์ตสองพอร์ตนี้ทีละตัว
พารามิเตอร์ Z
เราจะได้ชุดของสองสมการต่อไปนี้โดยพิจารณาตัวแปร V 1 & V 2ตามและ I 1 & I 2เป็นอิสระ ค่าสัมประสิทธิ์ของตัวแปรอิสระ I 1และ I 2เรียกว่าเป็นZ parameters.
$$ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $$
$$ V_2 = Z_ {21} I_1 + Z_ {22} I_2 $$
Z parameters คือ
$$ Z_ {11} = \ frac {V_1} {I_1}, \: เมื่อ \: I_2 = 0 $$
$$ Z_ {12} = \ frac {V_1} {I_2}, \: เมื่อ \: I_1 = 0 $$
$$ Z_ {21} = \ frac {V_2} {I_1}, \: เมื่อ \: I_2 = 0 $$
$$ Z_ {22} = \ frac {V_2} {I_2}, \: เมื่อ \: I_1 = 0 $$
พารามิเตอร์ Z เรียกว่าเป็น impedance parametersเพราะนี่เป็นเพียงอัตราส่วนของแรงดันไฟฟ้าและกระแส หน่วยของพารามิเตอร์ Z คือโอห์ม (Ω)
เราสามารถคำนวณพารามิเตอร์ Z สองตัวคือ Z 11และ Z 21โดยทำวงจรเปิดของพอร์ต 2 ในทำนองเดียวกันเราสามารถคำนวณพารามิเตอร์ Z อีกสองตัวคือ Z 12และ Z 22โดยทำวงจรเปิดของพอร์ต 1 ดังนั้นพารามิเตอร์ Z จึงเรียกอีกอย่างว่าopen-circuit impedance parameters.
พารามิเตอร์ Y
เราจะได้ชุดของสองสมการต่อไปนี้โดยพิจารณาตัวแปร I 1 & I 2ตามและ V 1 & V 2เป็นอิสระ ค่าสัมประสิทธิ์ของตัวแปรอิสระ V 1และ V 2เรียกว่าเป็นY parameters.
$$ I_1 = Y_ {11} V_1 + Y_ {12} V_2 $$
$$ I_2 = Y_ {21} V_1 + Y_ {22} V_2 $$
Y parameters คือ
$$ Y_ {11} = \ frac {I_1} {V_1}, \: เมื่อ \: V_2 = 0 $$
$$ Y_ {12} = \ frac {I_1} {V_2}, \: เมื่อ \: V_1 = 0 $$
$$ Y_ {21} = \ frac {I_2} {V_1}, \: เมื่อ \: V_2 = 0 $$
$$ Y_ {22} = \ frac {I_2} {V_2}, \: เมื่อ \: V_1 = 0 $$
พารามิเตอร์ Y เรียกว่าเป็น admittance parametersเพราะนี่เป็นเพียงอัตราส่วนของกระแสและแรงดันไฟฟ้า หน่วยของพารามิเตอร์ Y คือ mho
เราสามารถคำนวณพารามิเตอร์ Y สองตัวคือ Y 11และ Y 21โดยการลัดวงจรของพอร์ต 2 ในทำนองเดียวกันเราสามารถคำนวณพารามิเตอร์ Y อีกสองตัวคือ Y 12และ Y 22โดยการลัดวงจรของพอร์ต 1 ดังนั้นพารามิเตอร์ Y จึงถูกเรียกอีกอย่างว่าshort-circuit admittance parameters.
T พารามิเตอร์
เราจะได้ชุดของสองสมการต่อไปนี้โดยพิจารณาตัวแปร V 1 & I 1ตามและ V 2 & I 2เป็นอิสระ ค่าสัมประสิทธิ์ของ V 2และ -I 2เรียกว่าT parameters.
$$ V_1 = A V_2 - B I_2 $$
$$ I_1 = C V_2 - D I_2 $$
T parameters คือ
$$ A = \ frac {V_1} {V_2}, \: เมื่อ \: I_2 = 0 $$
$$ B = - \ frac {V_1} {I_2}, \: เมื่อ \: V_2 = 0 $$
$$ C = \ frac {I_1} {V_2}, \: เมื่อ \: I_2 = 0 $$
$$ D = - \ frac {I_1} {I_2}, \: เมื่อ \: V_2 = 0 $$
T พารามิเตอร์เรียกว่าพารามิเตอร์การส่งผ่านหรือ ABCD parameters. พารามิเตอร์ A และ D ไม่มีหน่วยใด ๆ เนื่องจากมีขนาดน้อยกว่า หน่วยของพารามิเตอร์ B และ C คือโอห์มและโมตามลำดับ
เราสามารถคำนวณพารามิเตอร์สองตัวคือ A และ C โดยทำวงจรเปิดของพอร์ต 2 ในทำนองเดียวกันเราสามารถคำนวณอีกสองพารามิเตอร์ B และ D โดยการลัดวงจรของพอร์ต 2
T 'พารามิเตอร์
เราจะได้ชุดของสองสมการต่อไปนี้โดยพิจารณาตัวแปร V 2 & I 2ตามและ V 1 & I 1เป็นอิสระ ค่าสัมประสิทธิ์ของ V 1และ -I 1เรียกว่าเป็นT’ parameters.
$$ V_2 = A 'V_1 - B' I_1 $$
$$ I_2 = C 'V_1 - D' I_1 $$
T’ parameters คือ
$$ A '= \ frac {V_2} {V_1}, \: เมื่อ \: I_1 = 0 $$
$$ B '= - \ frac {V_2} {I_1}, \: เมื่อ \: V_1 = 0 $$
$$ C '= \ frac {I_2} {V_1}, \: เมื่อ \: I_1 = 0 $$
$$ D '= - \ frac {I_2} {I_1}, \: เมื่อ \: V_1 = 0 $$
พารามิเตอร์ T 'เรียกว่าพารามิเตอร์การส่งผกผันหรือ A’B’C’D’ parameters. พารามิเตอร์ A 'และ D' ไม่มีหน่วยใด ๆ เนื่องจากมีขนาดน้อยกว่า หน่วยของพารามิเตอร์ B 'และ C' คือโอห์มและ Mho ตามลำดับ
เราสามารถคำนวณพารามิเตอร์สองตัวคือ A 'และ C' โดยทำวงจรเปิดของพอร์ต 1 ในทำนองเดียวกันเราสามารถคำนวณพารามิเตอร์อีกสองตัวคือ B 'และ D' โดยการลัดวงจรของพอร์ต 1
h- พารามิเตอร์
เราจะได้ชุดของสองสมการต่อไปนี้โดยพิจารณาตัวแปร V 1 & I 2ตามและ I 1 & V 2เป็นอิสระ ค่าสัมประสิทธิ์ของตัวแปรอิสระ I 1และ V 2เรียกว่าเป็นh-parameters.
$$ V_1 = h_ {11} I_1 + h_ {12} V_2 $$
$$ I_2 = h_ {21} I_1 + h_ {22} V_2 $$
พารามิเตอร์ h คือ
$$ h_ {11} = \ frac {V_1} {I_1}, \: เมื่อ \: V_2 = 0 $$
$$ h_ {12} = \ frac {V_1} {V_2}, \: เมื่อ \: I_1 = 0 $$
$$ h_ {21} = \ frac {I_2} {I_1}, \: เมื่อ \: V_2 = 0 $$
$$ h_ {22} = \ frac {I_2} {V_2}, \: เมื่อ \: I_1 = 0 $$
h- พารามิเตอร์เรียกว่าเป็น hybrid parameters. พารามิเตอร์ h 12และ h 21ไม่มีหน่วยใด ๆ เนื่องจากพารามิเตอร์เหล่านี้มีขนาดน้อย หน่วยของพารามิเตอร์ h 11และ h 22คือ Ohm และ Mho ตามลำดับ
เราสามารถคำนวณพารามิเตอร์สองตัวคือ h 11และ h 21โดยการลัดวงจรของพอร์ต 2 ในทำนองเดียวกันเราสามารถคำนวณพารามิเตอร์อีกสองตัวคือ h 12และ h 22โดยทำวงจรเปิดของพอร์ต 1
พารามิเตอร์ h หรือพารามิเตอร์ไฮบริดมีประโยชน์ในวงจรการสร้างแบบจำลองทรานซิสเตอร์ (เครือข่าย)
g- พารามิเตอร์
เราจะได้ชุดของสองสมการต่อไปนี้โดยพิจารณาตัวแปร I 1 & V 2ตามและ V 1 & I 2เป็นอิสระ ค่าสัมประสิทธิ์ของตัวแปรอิสระ V 1และ I 2เรียกว่าเป็นg-parameters.
$$ I_1 = g_ {11} V_1 + g_ {12} I_2 $$
$$ V_2 = g_ {21} V_1 + g_ {22} I_2 $$
g-parameters คือ
$$ g_ {11} = \ frac {I_1} {V_1}, \: เมื่อ \: I_2 = 0 $$
$$ g_ {12} = \ frac {I_1} {I_2}, \: เมื่อ \: V_1 = 0 $$
$$ g_ {21} = \ frac {V_2} {V_1}, \: เมื่อ \: I_2 = 0 $$
$$ g_ {22} = \ frac {V_2} {I_2}, \: เมื่อ \: V_1 = 0 $$
g-parameters เรียกว่าเป็น inverse hybrid parameters. พารามิเตอร์ g 12และ g 21ไม่มีหน่วยใด ๆ เนื่องจากพารามิเตอร์เหล่านี้มีขนาดน้อยกว่า หน่วยของพารามิเตอร์ g 11และ g 22คือ mho และ ohm ตามลำดับ
เราสามารถคำนวณพารามิเตอร์สองตัว g 11และ g 21โดยทำวงจรเปิดของพอร์ต 2 ในทำนองเดียวกันเราสามารถคำนวณอีกสองพารามิเตอร์ g 12และ g 22โดยการลัดวงจรของพอร์ต 1