ทฤษฎีเครือข่าย - ทฤษฎีบทการซ้อนทับ
Superposition theoremขึ้นอยู่กับแนวคิดของความเป็นเชิงเส้นระหว่างการตอบสนองและการกระตุ้นของวงจรไฟฟ้า ระบุว่าการตอบสนองในสาขาเฉพาะของวงจรเชิงเส้นเมื่อแหล่งที่มาอิสระหลายแหล่งทำหน้าที่ในเวลาเดียวกันจะเทียบเท่ากับผลรวมของการตอบสนองเนื่องจากแหล่งที่มาอิสระแต่ละแหล่งทำหน้าที่ในแต่ละครั้ง
ในวิธีนี้เราจะพิจารณาเฉพาะ one independent sourceขณะนั้น. ดังนั้นเราต้องกำจัดแหล่งที่มาอิสระที่เหลือออกจากวงจร เราสามารถกำจัดแหล่งกำเนิดแรงดันไฟฟ้าโดยการทำให้ขั้วทั้งสองสั้นลงและในทำนองเดียวกันแหล่งกำเนิดกระแสไฟฟ้าโดยการเปิดขั้วทั้งสอง
ดังนั้นเราจำเป็นต้องค้นหาการตอบสนองในสาขาใดสาขาหนึ่ง ‘n’ timesหากมีแหล่งที่มาที่เป็นอิสระ 'n' การตอบสนองในสาขาหนึ่งอาจเป็นได้ทั้งกระแสที่ไหลผ่านสาขานั้นหรือแรงดันไฟฟ้าข้ามสาขานั้น
ขั้นตอนของทฤษฎีบทการซ้อนทับ
ทำตามขั้นตอนเหล่านี้เพื่อค้นหาการตอบสนองในสาขาหนึ่ง ๆ โดยใช้ทฤษฎีบทซ้อนทับ
Step 1 - ค้นหาการตอบสนองในสาขาใดสาขาหนึ่งโดยพิจารณาแหล่งที่มาอิสระหนึ่งแหล่งและกำจัดแหล่งข้อมูลอิสระที่เหลืออยู่ในเครือข่าย
Step 2 - ทำซ้ำขั้นตอนที่ 1 สำหรับแหล่งข้อมูลอิสระทั้งหมดที่มีอยู่ในเครือข่าย
Step 3 - เพิ่มการตอบกลับทั้งหมดเพื่อให้ได้รับการตอบสนองโดยรวมในสาขาหนึ่ง ๆ เมื่อมีแหล่งข้อมูลอิสระทั้งหมดอยู่ในเครือข่าย
ตัวอย่าง
ค้นหากระแสที่ไหลผ่านตัวต้านทาน 20 Ωของวงจรต่อไปนี้โดยใช้ superposition theorem.
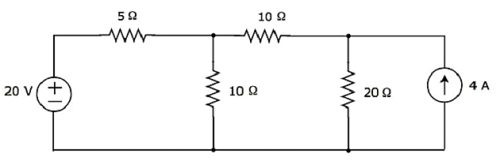
Step 1 - ให้เราหากระแสที่ไหลผ่านตัวต้านทาน 20 Ωโดยพิจารณาเฉพาะ 20 V voltage source. ในกรณีนี้เราสามารถกำจัดแหล่งจ่ายกระแส 4 A ได้โดยการสร้างวงจรเปิด แผนภาพวงจรที่แก้ไขจะแสดงในรูปต่อไปนี้

มีโหนดหลักเพียงโหนดเดียวยกเว้นกราวด์ในวงจรด้านบน ดังนั้นเราสามารถใช้nodal analysisวิธี. แรงดันไฟฟ้าของโหนด V 1มีป้ายกำกับในรูปต่อไปนี้ ที่นี่ V 1คือแรงดันไฟฟ้าจากโหนด 1 เทียบกับกราวด์
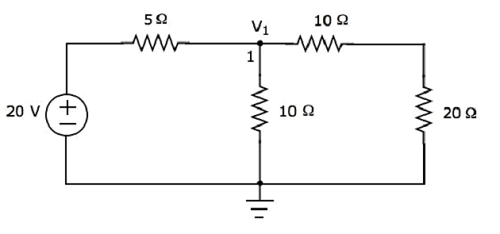
nodal equation ที่โหนด 1 คือ
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$
$$ \ Rightarrow \ frac {6V_1 - 120 + 3V_1 + V_1} {30} = 0 $$
$$ \ Rightarrow 10V_1 = 120 $$
$$ \ Rightarrow V_1 = 12V $$
current flowing through 20 Ω resistor สามารถพบได้โดยการทำให้เข้าใจง่ายต่อไปนี้
$$ I_1 = \ frac {V_1} {10 + 20} $$
แทนค่าของ V 1ในสมการด้านบน
$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0.4 A $$
ดังนั้นกระแสที่ไหลผ่านตัวต้านทาน 20 Ωคือ 0.4 Aเมื่อพิจารณาแหล่งจ่ายแรงดันไฟฟ้าเพียง 20 V
Step 2 - ให้เราหากระแสที่ไหลผ่านตัวต้านทาน 20 Ωโดยพิจารณาเฉพาะ 4 A current source. ในกรณีนี้เราสามารถกำจัดแหล่งจ่ายแรงดันไฟฟ้า 20 V ได้โดยการลัดวงจรของมัน แผนภาพวงจรที่แก้ไขจะแสดงในรูปต่อไปนี้
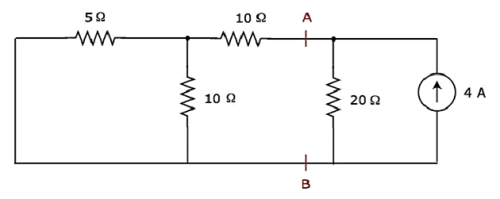
ในวงจรด้านบนมีตัวต้านทานสามตัวทางด้านซ้ายของขั้ว A & B เราสามารถแทนที่ตัวต้านทานเหล่านี้ด้วยตัวเดียว equivalent resistor. ที่นี่ตัวต้านทาน 5 Ωและ 10 Ωเชื่อมต่อแบบขนานและชุดค่าผสมทั้งหมดอยู่ในอนุกรมที่มีตัวต้านทาน 10 Ω
equivalent resistance ทางด้านซ้ายของเทอร์มินัล A & B จะเป็น
$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
แผนภาพวงจรแบบง่ายแสดงในรูปต่อไปนี้
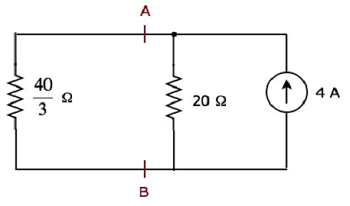
เราสามารถหากระแสที่ไหลผ่านตัวต้านทาน 20 Ωโดยใช้ current division principle.
$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
แทนที่ $ I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega $ และ $ R_2 = 20 \ Omega $ ในสมการด้านบน
$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1.6 A $$
ดังนั้นกระแสที่ไหลผ่านตัวต้านทาน 20 Ωคือ 1.6 Aเมื่อพิจารณาแหล่งที่มาปัจจุบันเพียง 4 A
Step 3 - เราจะได้กระแสที่ไหลผ่านตัวต้านทาน 20 Ωของวงจรที่กำหนดโดยทำ addition of two currents ที่เราได้รับในขั้นตอนที่ 1 และขั้นตอนที่ 2 ในทางคณิตศาสตร์สามารถเขียนเป็น
$$ I = I_1 + I_2 $$
แทนค่าของI 1และI 2ในสมการด้านบน
$$ I = 0.4 + 1.6 = 2 A $$
ดังนั้นกระแสที่ไหลผ่านตัวต้านทาน 20 Ωของวงจรที่กำหนดคือ 2 A.
Note - เราไม่สามารถใช้ทฤษฎีบทการซ้อนทับโดยตรงเพื่อหาจำนวน powerส่งไปยังตัวต้านทานใด ๆ ที่มีอยู่ในวงจรเชิงเส้นเพียงแค่ทำการเพิ่มกำลังที่ส่งไปยังตัวต้านทานนั้นเนื่องจากแหล่งที่มาอิสระแต่ละแหล่ง แต่เราสามารถคำนวณกระแสทั้งหมดที่ไหลผ่านหรือแรงดันไฟฟ้าข้ามตัวต้านทานนั้นโดยใช้ทฤษฎีบทการซ้อนทับและจากนั้นเราสามารถคำนวณปริมาณพลังงานที่ส่งไปยังตัวต้านทานนั้นโดยใช้ $ I ^ 2 R $ หรือ $ \ frac {V ^ 2} {R} $.