ทฤษฎีเครือข่าย - การวิเคราะห์ตาข่าย

ในการวิเคราะห์ตาข่ายเราจะพิจารณากระแสที่ไหลผ่านแต่ละตาข่าย ดังนั้นการวิเคราะห์ตาข่ายจึงเรียกอีกอย่างว่าMesh-current method.

ก branchเป็นเส้นทางที่รวมสองโหนดและมีองค์ประกอบวงจร หากกิ่งไม้เป็นของตาข่ายเพียงเส้นเดียวกระแสของกิ่งจะเท่ากับกระแสตาข่าย

หากกิ่งไม้เป็นแบบเดียวกันกับสองตาข่ายกระแสของกิ่งจะเท่ากับผลรวม (หรือผลต่าง) ของกระแสตาข่ายสองเส้นเมื่ออยู่ในทิศทางเดียวกัน (หรือตรงกันข้าม)

ขั้นตอนของการวิเคราะห์ตาข่าย

ทำตามขั้นตอนเหล่านี้ในขณะที่แก้ปัญหาเครือข่ายไฟฟ้าหรือวงจรโดยใช้การวิเคราะห์ตาข่าย

Step 1 - ระบุไฟล์ meshes และติดป้ายกระแสตาข่ายในทิศทางตามเข็มนาฬิกาหรือทวนเข็มนาฬิกา
Step 2 - สังเกตปริมาณของกระแสที่ไหลผ่านแต่ละองค์ประกอบในรูปของกระแสตาข่าย
Step 3 - เขียน mesh equationsกับตาข่ายทั้งหมด สมการตาข่ายได้มาจากการใช้ KVL ก่อนแล้วตามด้วยกฎของโอห์ม
Step 4 - แก้สมการตาข่ายที่ได้รับในขั้นตอนที่ 3 เพื่อรับไฟล์ mesh currents.

ตอนนี้เราสามารถค้นหากระแสที่ไหลผ่านองค์ประกอบใด ๆ และแรงดันไฟฟ้าผ่านองค์ประกอบใด ๆ ที่มีอยู่ในเครือข่ายที่กำหนดโดยใช้กระแสตาข่าย

ตัวอย่าง

ค้นหาแรงดันไฟฟ้าข้ามตัวต้านทาน 30 Ωโดยใช้ Mesh analysis.

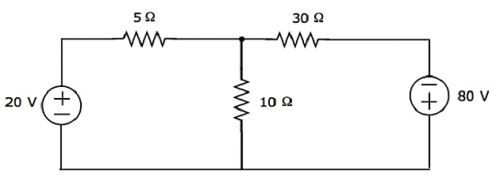
Step 1- มีสองตาข่ายในวงจรด้านบน mesh currentsI ₁และ I ₂ถือเป็นทิศทางตามเข็มนาฬิกา กระแสตาข่ายเหล่านี้แสดงในรูปต่อไปนี้

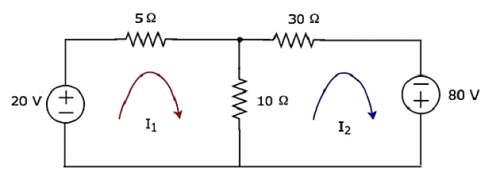
Step 2- กระแสตาข่าย I ₁ไหลผ่านแหล่งจ่ายแรงดัน 20 V และตัวต้านทาน 5 Ω ในทำนองเดียวกันกระแสตาข่าย I ₂ไหลผ่านตัวต้านทาน 30 Ωและแหล่งแรงดันไฟฟ้า -80 V แต่ความแตกต่างของกระแสตาข่ายสองเส้นคือ I ₁และ I ₂ไหลผ่านตัวต้านทาน 10 Ωเนื่องจากเป็นกิ่งก้านทั่วไปของตาข่ายสองเส้น

Step 3 - ในกรณีนี้เราจะได้รับ two mesh equationsเนื่องจากมีสองตาข่ายในวงจรที่กำหนด เมื่อเราเขียนสมการตาข่ายสมมติว่ากระแสตาข่ายของตาข่ายนั้นมากกว่ากระแสตาข่ายอื่น ๆ ทั้งหมดของวงจร

mesh equation ของตาข่ายแรกคือ

$20 - 5 I_{1} - 10 (I_{1} - I_{2}) = 0$

$R i g h t a r r o w 20 - 15 I_{1} + 10 I_{2} = 0$

$R i g h t a r r o w 10 I_{2} = 15 I_{1} - 20$

หารสมการข้างบนด้วย 5

$2 I_{2} = 3 I_{1} - 4$

คูณสมการข้างบนด้วย 2

$4 I_{2} = 6 I_{1} - 8$ Equation 1

mesh equation ของตาข่ายที่สองคือ

$- 10 (I_{2} - I_{1}) - 30 I_{2} + 80 = 0$

หารสมการข้างบนด้วย 10

$- (I_{2} - I_{1}) - 3 I_{2} + 8 = 0$

$R i g h t a r r o w - 4 I_{2} + I_{1} + 8 = 0$

$4 I_{2} = I_{1} + 8$ Equation 2

Step 4- การหากระแสตาข่ายI ₁และI ₂โดยการแก้สมการ 1 และสมการ 2

เงื่อนไขด้านซ้ายมือของสมการ 1 และสมการ 2 จะเหมือนกัน จึงถือเอาข้อตกลงทางด้านขวามือของสมการที่ 1 และ 2 สมการเพื่อหาค่าของฉัน 1

$6 I_{1} - 8 = I_{1} + 8$

$R i g h t a r r o w 5 I_{1} = 16$

$R i g h t a r r o w I_{1} = f r a c 165 A$

แทนค่าI ₁ในสมการ 2

$4 I_{2} = f r a c 165 + 8$

$R i g h t a r r o w 4 I_{2} = f r a c 565$

$R i g h t a r r o w I_{2} = f r a c 145 A$

เราจึงได้กระแสตาข่ายI ₁และI ₂เป็น $m a t h b f f r a c 165$ A และ $m a t h b f f r a c 145$ A ตามลำดับ

Step 5- กระแสที่ไหลผ่านตัวต้านทาน 30 Ωไม่ใช่อะไรนอกจากกระแสตาข่ายI ₂และเท่ากับ $f r a c 145$ A ตอนนี้เราสามารถหาแรงดันไฟฟ้าข้ามตัวต้านทาน 30 Ωได้โดยใช้กฎของโอห์ม

$V_{30 O m e g a} = I_{2} R$

แทนค่าของI ₂และRในสมการด้านบน

$V_{30 O m e g a} = l g r o u p f r a c 145 r g r o u p 30$

$R i g h t a r r o w V_{30 O m e g a} = 84 V$

ดังนั้นแรงดันไฟฟ้าข้ามตัวต้านทาน 30 Ωของวงจรที่กำหนดคือ 84 V.

Note 1- จากตัวอย่างข้างต้นเราสามารถสรุปได้ว่าเราต้องแก้สมการเมช 'm' ถ้าวงจรไฟฟ้ามีตาข่าย 'm' นั่นเป็นเหตุผลที่เราสามารถเลือกการวิเคราะห์ตาข่ายเมื่อจำนวนตาข่ายน้อยกว่าจำนวนโหนดหลัก (ยกเว้นโหนดอ้างอิง) ของวงจรไฟฟ้าใด ๆ

Note 2 - เราสามารถเลือกการวิเคราะห์โหนดหรือการวิเคราะห์แบบเมชเมื่อจำนวนตาข่ายเท่ากับจำนวนโหนดหลัก (ยกเว้นโหนดอ้างอิง) ในวงจรไฟฟ้าใด ๆ