डिजिटल सिग्नल प्रोसेसिंग - त्वरित गाइड
परिभाषा
कुछ भी जो सूचना को वहन करता है उसे संकेत कहा जा सकता है। इसे एक भौतिक मात्रा के रूप में भी परिभाषित किया जा सकता है जो समय, तापमान, दबाव या किसी स्वतंत्र चर जैसे कि भाषण संकेत या वीडियो सिग्नल के साथ बदलता रहता है।
ऑपरेशन की प्रक्रिया जिसमें एक संकेत (आयाम, आकार, चरण, आवृत्ति, आदि) की विशेषताओं में परिवर्तन होता है, सिग्नल प्रोसेसिंग के रूप में जाना जाता है।
Note- मुख्य संकेत के साथ हस्तक्षेप करने वाले किसी भी अवांछित सिग्नल को शोर कहा जाता है। तो, शोर भी एक संकेत है लेकिन अवांछित है।
उनके प्रतिनिधित्व और प्रसंस्करण के अनुसार, संकेतों को विभिन्न श्रेणियों के विवरण में वर्गीकृत किया जा सकता है जिनमें से नीचे चर्चा की गई है।
निरंतर समय संकेत
निरंतर-समय संकेतों को समय की एक निरंतरता के साथ परिभाषित किया जाता है और इस प्रकार, एक निरंतर स्वतंत्र चर द्वारा दर्शाया जाता है। निरंतर-समय संकेतों को अक्सर एनालॉग संकेतों के रूप में संदर्भित किया जाता है।
इस प्रकार का संकेत आयाम और समय दोनों में निरंतरता दर्शाता है। प्रत्येक समय में इनका मान होगा। निरंतर समय संकेत के साइन और कोसाइन कार्य सबसे अच्छे उदाहरण हैं।
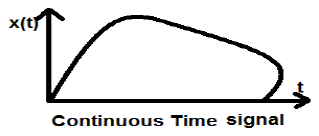
ऊपर दिखाया गया संकेत निरंतर समय संकेत का एक उदाहरण है क्योंकि हम प्रत्येक समय पर संकेत का मूल्य प्राप्त कर सकते हैं।
असतत समय संकेत
असतत समय पर परिभाषित होने वाले संकेतों को असतत संकेतों के रूप में जाना जाता है। इसलिए, प्रत्येक स्वतंत्र चर का अलग मूल्य है। इस प्रकार, उन्हें संख्याओं के अनुक्रम के रूप में दर्शाया जाता है।
यद्यपि भाषण और वीडियो संकेतों को निरंतर और असतत समय प्रारूप दोनों में प्रतिनिधित्व करने का विशेषाधिकार है; कुछ परिस्थितियों में, वे समान हैं। एम्पलीट्यूड भी असतत विशेषताओं को दर्शाता है। इसका सटीक उदाहरण एक डिजिटल सिग्नल है; जिसका आयाम और समय दोनों असतत हैं।
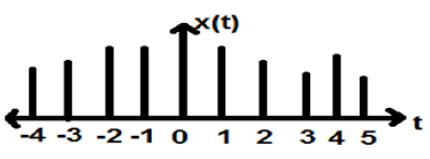
ऊपर दिए गए चित्र में एक असतत संकेत की असतत आयाम विशेषता दर्शाया गया है। गणितीय रूप से, इन प्रकार के संकेतों को औपचारिक रूप दिया जा सकता है;
$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$जहाँ, n एक पूर्णांक है।
यह संख्या x का एक क्रम है, जहां अनुक्रम में n वें नंबर को x [n] के रूप में दर्शाया जाता है।
एक प्रणाली का परीक्षण करने के लिए, आम तौर पर, मानक या बुनियादी संकेतों का उपयोग किया जाता है। ये सिग्नल कई जटिल संकेतों के लिए बुनियादी बिल्डिंग ब्लॉक हैं। इसलिए, वे संकेतों और प्रणालियों के अध्ययन में बहुत महत्वपूर्ण भूमिका निभाते हैं।
यूनिट आवेग या डेल्टा समारोह
एक संकेत, जो स्थिति को संतुष्ट करता है, $\delta(t) = \lim_{\epsilon \to \infty} x(t)$इकाई आवेग संकेत के रूप में जाना जाता है। यह संकेत अनंतता में जाता है जब t = 0 और शून्य पर जाता है जब t that 0 ऐसा होता है कि इसके वक्र के नीचे का क्षेत्र हमेशा एक के बराबर होता है। डेल्टा फ़ंक्शन में हर जगह पर शून्य आयाम है excunit_impulse.jpgept पर t = 0।

यूनिट आवेग संकेत के गुण
- δ (t) एक सम संकेत है।
- δ (t) न तो ऊर्जा और न ही पावर (NENP) सिग्नल का एक उदाहरण है।
- इकाई आवेग संकेत के क्षेत्र के रूप में लिखा जा सकता है; $$A = \int_{-\infty}^{\infty} \delta (t)dt = \int_{-\infty}^{\infty} \lim_{\epsilon \to 0} x(t) dt = \lim_{\epsilon \to 0} \int_{-\infty}^{\infty} [x(t)dt] = 1$$
- संकेत के वजन या ताकत के रूप में लिखा जा सकता है; $$y(t) = A\delta (t)$$
- भारित आवेग संकेत के क्षेत्र के रूप में लिखा जा सकता है - $$y (t) = \int_{-\infty}^{\infty} y (t)dt = \int_{-\infty}^{\infty} A\delta (t) = A[\int_{-\infty}^{\infty} \delta (t)dt ] = A = 1 = Wigthedimpulse$$
यूनिट स्टेप सिग्नल
एक संकेत, जो निम्नलिखित दो स्थितियों को संतुष्ट करता है -
- $U(t) = 1(when\quad t \geq 0 )and$
- $U(t) = 0 (when\quad t < 0 )$
एक इकाई चरण संकेत के रूप में जाना जाता है।
इसमें t = 0. पर असंतोष दिखाने की संपत्ति है। असंतोष के बिंदु पर, सिग्नल मूल्य औसत संकेत मूल्य द्वारा दिया जाता है। यह संकेत विच्छेदन के बिंदु के ठीक पहले और बाद में लिया गया है (गिब के फेनोमेना के अनुसार)।
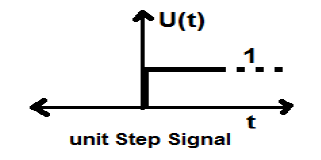
यदि हम एक और कदम सिग्नल को एक कदम संकेत जोड़ते हैं जो समय स्केल किया जाता है, तो परिणाम एकता होगा। यह एक पावर टाइप सिग्नल है और पावर का मान 0.5 है। RMS (रूट माध्य वर्ग) मान 0.707 है और इसका औसत मान भी 0.5 है
रैंप सिग्नल
एक रैंप सिग्नल में चरण सिग्नल परिणाम का एकीकरण। इसे r (t) द्वारा दर्शाया गया है। रैंप सिग्नल भी स्थिति को संतुष्ट करता है$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$। यह न तो ऊर्जा है और न ही पावर (एनईएनपी) टाइप सिग्नल है।
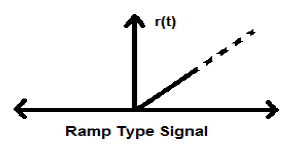
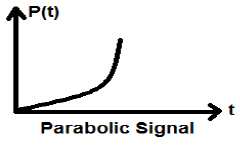
परवलयिक संकेत
रैंप सिग्नल के एकीकरण से पैराबोलिक सिग्नल होता है। यह p (t) द्वारा दर्शाया गया है। परवलयिक संकेत भी स्थिति को संतुष्ट करता है$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$। यह न तो ऊर्जा है और न ही पावर (एनईएनपी) टाइप सिग्नल है।
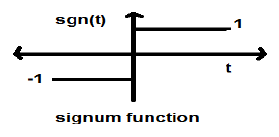
सिग्नम फंक्शन
इस फ़ंक्शन को इस रूप में दर्शाया गया है
$$sgn(t) = \begin{cases}1 & for\quad t >0\\-1 & for\quad t<0\end{cases}$$यह एक पावर टाइप सिग्नल है। इसका पावर मान और RMS (रूट माध्य वर्ग) मान, दोनों हैं। 1. साइनम फ़ंक्शन का औसत मान शून्य है।
Sinc फ़ंक्शन
यह साइन का कार्य भी है और इसे इस प्रकार लिखा जाता है -
$$SinC(t) = \frac{Sin\Pi t}{\Pi T} = Sa(\Pi t)$$Sinc फ़ंक्शन के गुण
यह एक ऊर्जा प्रकार का संकेत है।
$Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$
$Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$ (पाप की सीमा -1 से +1 के बीच भिन्न होती है लेकिन अनंत द्वारा विभाजित कुछ भी शून्य के बराबर है)
-
अगर $ \sin c(t) = 0 => \sin \Pi t = 0$
$\Rightarrow \Pi t = n\Pi$
$\Rightarrow t = n (n \neq 0)$
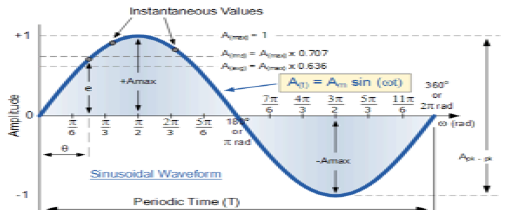
साइनसोइडल सिग्नल
एक संकेत, जो प्रकृति में निरंतर है, निरंतर संकेत के रूप में जाना जाता है। एक साइनसोइडल सिग्नल का सामान्य प्रारूप है
$$x(t) = A\sin (\omega t + \phi )$$यहाँ,
संकेत का एक = आयाम
ω = संकेत की कोणीय आवृत्ति (रेडियंस में मापी गई)
φ = संकेत का चरण कोण (रेडियंस में मापा गया)
इस संकेत की प्रवृत्ति निश्चित अवधि के बाद खुद को दोहराना है, इसलिए इसे आवधिक संकेत कहा जाता है। संकेत की समय अवधि इस प्रकार दी गई है;
$$T = \frac{2\pi }{\omega }$$साइनसॉइडल सिग्नल का आरेखीय दृश्य नीचे दिखाया गया है।
आयताकार कार्य
एक संकेत को आयताकार फ़ंक्शन प्रकार कहा जाता है यदि यह निम्न स्थिति को संतुष्ट करता है -
$$\pi(\frac{t}{\tau}) = \begin{cases}1, & for\quad t\leq \frac{\tau}{2}\\0, & Otherwise\end{cases}$$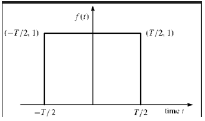
Y- अक्ष के बारे में सममित होने के नाते, इस संकेत को संकेत भी कहा जाता है।
त्रिकोणीय पल्स सिग्नल
कोई भी संकेत, जो निम्न स्थिति को संतुष्ट करता है, त्रिकोणीय संकेत के रूप में जाना जाता है।
$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & for|t|<\frac{\tau}{2}\\0 & for|t|>\frac{\tau}{2}\end{cases}$$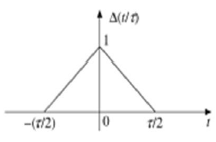
यह संकेत Y- अक्ष के बारे में सममित है। इसलिए, इसे संकेत भी कहा जाता है।
हमने देखा है कि कंटिन्युअस टाइम डोमेन में बेसिक सिग्नल्स को कैसे दर्शाया जा सकता है। आइए देखते हैं कि असतत समय डोमेन में मूल संकेतों का प्रतिनिधित्व कैसे किया जा सकता है।
यूनिट आवेग अनुक्रम
इसे असतत समय डोमेन में δ (n) के रूप में दर्शाया गया है और इसे परिभाषित किया जा सकता है;
$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$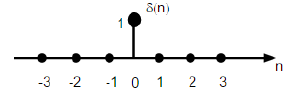
यूनिट स्टेप सिग्नल
असतत समय इकाई चरण संकेत के रूप में परिभाषित किया गया है;
$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$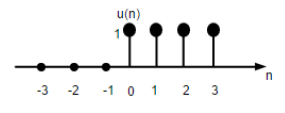
ऊपर दिया गया आंकड़ा एक असतत चरण फ़ंक्शन के चित्रमय प्रतिनिधित्व को दर्शाता है।
यूनिट रैंप फंक्शन
एक असतत इकाई रैंप फ़ंक्शन को निम्न के रूप में परिभाषित किया जा सकता है -
$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$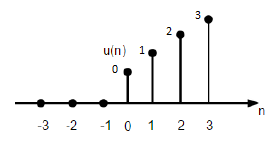
ऊपर दिया गया आंकड़ा एक असतत रैंप सिग्नल के चित्रमय प्रतिनिधित्व को दर्शाता है।
परवलयिक क्रिया
असतत इकाई परवलयिक क्रिया को p (n) के रूप में निरूपित किया जाता है और इसे परिभाषित किया जा सकता है;
$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$यूनिट स्टेप फंक्शन के संदर्भ में इसे लिखा जा सकता है;
$$P(n) = \frac{n^{2}}{2}U(n)$$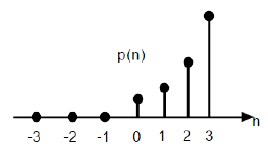
ऊपर दिया गया आंकड़ा एक परवलयिक अनुक्रम के चित्रमय प्रतिनिधित्व को दर्शाता है।
साइनसोइडल सिग्नल
सभी निरंतर-समय के संकेत आवधिक हैं। असतत समय साइनसोइडल अनुक्रम आवधिक हो सकते हैं या नहीं। वे ω के मूल्य पर निर्भर करते हैं। असतत समय संकेत समय-समय पर होने के लिए, कोणीय आवृत्ति π 2π का एक तर्कसंगत बहु होना चाहिए।
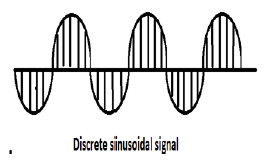
ऊपर की आकृति में एक असतत साइनसोइडल संकेत दिखाया गया है।
साइनसोइडल सिग्नल के असतत रूप को प्रारूप में दर्शाया जा सकता है -
$$x(n) = A\sin(\omega n + \phi)$$यहाँ A, n और φ का सामान्य अर्थ है और n पूर्णांक है। असतत साइनसोइडल सिग्नल की समय अवधि किसके द्वारा दी गई है -
$$N =\frac{2\pi m}{\omega}$$जहाँ, N और m पूर्णांक हैं।
संकेतों पर किए गए विभिन्न परिस्थितियों या संचालन के अनुसार निरंतर समय संकेतों को वर्गीकृत किया जा सकता है।
यहां तक कि और विषम संकेत
यहां तक कि सिग्नल भी
एक संकेत के लिए कहा जाता है भले ही यह निम्नलिखित स्थिति को संतुष्ट करता है;
$$x(-t) = x(t)$$संकेत के समय उलट यहाँ आयाम पर किसी भी परिवर्तन का मतलब नहीं है। उदाहरण के लिए, नीचे दिखाए गए त्रिकोणीय लहर पर विचार करें।
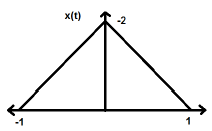
त्रिकोणीय संकेत एक भी संकेत है। चूंकि, यह Y- अक्ष के बारे में सममित है। हम कह सकते हैं कि यह Y- अक्ष के बारे में दर्पण छवि है।
नीचे दिए गए चित्र में दिखाए गए अनुसार एक और संकेत पर विचार करें।
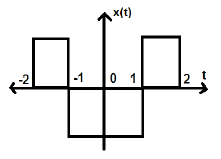
हम देख सकते हैं कि उपरोक्त संकेत यहां तक कि जैसे कि यह Y- अक्ष के बारे में सममित है।
अजीब संकेत
एक संकेत को विषम कहा जाता है, अगर यह निम्नलिखित स्थिति को संतुष्ट करता है
$$x(-t) = -x(t)$$यहाँ, दोनों समय उलट और आयाम परिवर्तन एक साथ होते हैं।
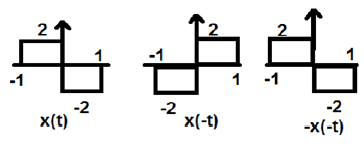
ऊपर दिए गए चित्र में, हम एक चरण सिग्नल x (t) देख सकते हैं। यह जांचने के लिए कि यह एक अजीब संकेत है या नहीं, पहले हम समय उलटा करते हैं अर्थात x (-t) और परिणाम जैसा कि चित्र में दिखाया गया है। फिर हम परिणामी संकेत के आयाम को उल्टा करते हैं - (-x) और हम परिणाम प्राप्त करते हैं जैसा कि चित्र में दिखाया गया है।
यदि हम पहली और तीसरी तरंग की तुलना करते हैं, तो हम देख सकते हैं कि वे समान हैं, अर्थात x (t) = -x (-t), जो हमारे मानदंड को संतुष्ट करता है। इसलिए, उपरोक्त संकेत एक अजीब संकेत है।
सम और विषम संकेतों से संबंधित कुछ महत्वपूर्ण परिणाम नीचे दिए गए हैं।
- यहाँ तक कि × सम =
- विषम × विषम = सम
- यहां तक कि × विषम = विषम
- सम Even सम = भी
- विषम ± विषम = विषम
- सम = विषम = न भी विषम
सम या विषम रूप में किसी भी संकेत का प्रतिनिधित्व
कुछ संकेतों को सीधे या विषम प्रकार में वर्गीकृत नहीं किया जा सकता है। इन्हें सम और विषम संकेत दोनों के संयोजन के रूप में दर्शाया गया है।
$$x(t)\rightarrow x_{e}(t)+x_{0}(t)$$जहाँ x e (t) सम संकेत का प्रतिनिधित्व करता है और x o (t) विषम संकेत का प्रतिनिधित्व करता है
$$x_{e}(t)=\frac{[x(t)+x(-t)]}{2}$$तथा
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$उदाहरण
संकेत के सम और विषम भाग ज्ञात कीजिए $x(n) = t+t^{2}+t^{3}$
Solution - एक्स (एन) को उलटने से, हमें मिलता है
$$x(-n) = -t+t^{2}-t^{3}$$
अब, सूत्र के अनुसार, समान भाग
$$x_{e}(t) = \frac{x(t)+x(-t)}{2}$$
$$= \frac{[(t+t^{2}+t^{3})+(-t+t^{2}-t^{3})]}{2}$$
$$= t^{2}$$
इसी तरह, सूत्र के अनुसार विषम भाग है
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$
$$= \frac{[(t+t^{2}+t^{3})-(-t+t^{2}-t^{3})]}{2}$$
$$= t+t^{3}$$
आवधिक और गैर-आवधिक संकेत
आवधिक संकेत
समय-समय पर निश्चित अंतराल के बाद आवधिक संकेत दोहराता है। हम इसे समीकरण रूप में दिखा सकते हैं -
$$x(t) = x(t)\pm nT$$जहां, n = एक पूर्णांक (1,2,3 ……)
टी = मौलिक समय अवधि (एफ़टीपी) ≠ 0 और time time
मौलिक समय अवधि (एफ़टीपी) समय का सबसे छोटा सकारात्मक और निश्चित मूल्य है जिसके लिए संकेत आवधिक है।
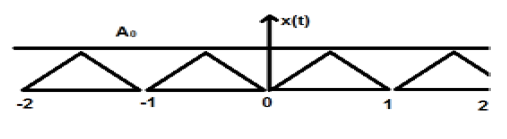
आयाम ए के ऊपर एक त्रिकोणीय संकेत दिखाया गया है। यहां, संकेत हर 1 सेकंड के बाद दोहरा रहा है। इसलिए, हम कह सकते हैं कि संकेत आवधिक है और इसका एफ़टीपी 1 सेकंड है।
गैर-आवधिक संकेत
बस, हम कह सकते हैं, संकेत, जो आवधिक नहीं हैं प्रकृति में गैर-आवधिक हैं। स्पष्ट रूप से, ये संकेत किसी भी अंतराल समय के बाद खुद को दोहराएंगे नहीं।
गैर-आवधिक संकेत एक निश्चित प्रारूप का पालन नहीं करते हैं; इसलिए, कोई विशेष गणितीय समीकरण उनका वर्णन नहीं कर सकता है।
ऊर्जा और पावर सिग्नल
एक संकेत को एक ऊर्जा संकेत कहा जाता है, यदि और केवल अगर, निहित कुल ऊर्जा परिमित और गैर-शून्य (0 <ई <<) है। इसलिए, किसी भी ऊर्जा प्रकार के संकेत के लिए, कुल सामान्यीकृत संकेत परिमित और गैर-शून्य है।
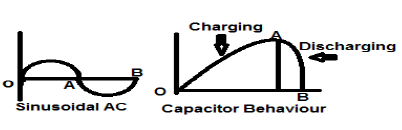
एक साइनसोइडल एसी वर्तमान संकेत ऊर्जा प्रकार संकेत का एक आदर्श उदाहरण है क्योंकि यह एक मामले में सकारात्मक आधा चक्र में है और फिर अगले आधे चक्र में नकारात्मक है। इसलिए, इसकी औसत शक्ति शून्य हो जाती है।
एक दोषरहित संधारित्र भी ऊर्जा प्रकार संकेत का एक आदर्श उदाहरण है क्योंकि जब यह स्रोत से जुड़ा होता है तो यह अपने इष्टतम स्तर तक चार्ज करता है और जब स्रोत को हटा दिया जाता है, तो यह एक लोड के माध्यम से ऊर्जा की समान मात्रा को नष्ट कर देता है और अपनी औसत शक्ति बनाता है। शून्य।
किसी भी परिमित संकेत x (t) के लिए ऊर्जा को E के रूप में दर्शाया जा सकता है और इसे लिखा जाता है;
$$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$ऊर्जा प्रकार के संकेतों का स्पेक्ट्रल घनत्व विभिन्न आवृत्ति स्तरों पर वितरित ऊर्जा की मात्रा देता है।
पावर टाइप सिग्नल
एक सिग्नल को पावर टाइप सिग्नल कहा जाता है, यदि और केवल अगर, सामान्यीकृत औसत शक्ति परिमित और गैर-शून्य है (यानी <p <be)। पावर टाइप सिग्नल के लिए, सामान्यीकृत औसत शक्ति परिमित और गैर-शून्य है। लगभग सभी आवधिक संकेत पावर सिग्नल हैं और उनकी औसत शक्ति परिमित और गैर-शून्य है।
गणितीय रूप में, एक सिग्नल x (टी) की शक्ति के रूप में लिखा जा सकता है;
$$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$ऊर्जा और पावर सिग्नल के बीच अंतर
निम्न तालिका ऊर्जा और पावर सिग्नल के अंतर को सारांशित करती है।
| पावर सिग्नल | ऊर्जा संकेत |
|---|---|
| व्यावहारिक आवधिक संकेत शक्ति संकेत हैं। | गैर-आवधिक संकेत ऊर्जा संकेत हैं। |
| यहां, सामान्यीकृत औसत शक्ति परिमित और गैर-शून्य है। | यहां, कुल सामान्यीकृत ऊर्जा परिमित और गैर-शून्य है। |
| गणित के अनुसार, $$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$ |
गणित के अनुसार, $$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$ |
| इन संकेतों का अस्तित्व समय के साथ अनंत है। | ये संकेत सीमित समय के लिए मौजूद हैं। |
| पावर सिग्नल की ऊर्जा अनंत समय पर अनंत है। | ऊर्जा सिग्नल की शक्ति अनंत समय से अधिक शून्य है। |
हल के उदाहरण
Example 1 - एक संकेत की शक्ति का पता लगाएं $z(t) = 2\cos(3\Pi t+30^{o})+4\sin(3\Pi +30^{o})$
Solution- उपर्युक्त दो संकेत एक-दूसरे के लिए ऑर्थोगोनल हैं क्योंकि उनकी आवृत्ति की शर्तें एक-दूसरे के समान होती हैं, उनमें भी समान चरण अंतर होता है। तो, कुल शक्ति व्यक्तिगत शक्तियों का योग होगी।
लश्कर $z(t) = x(t)+y(t)$
कहाँ पे $x(t) = 2\cos (3\Pi t+30^{o})$ तथा $y(t) = 4\sin(3\Pi +30^{o})$
का बल $x(t) = \frac{2^{2}}{2} = 2$
का बल $y(t) = \frac{4^{2}}{2} = 8$
इसलिए, $P(z) = p(x)+p(y) = 2+8 = 10$... उत्तर:।
Example 2 - दिए गए संकेत का परीक्षण करें $x(t) = t^{2}+j\sin t$ संयुग्म है या नहीं?
Solution- यहाँ, t 2 का वास्तविक भाग सम और विषम भाग (काल्पनिक) है$\sin t$अजीब है। तो उपरोक्त संकेत Conjugate सिग्नल है।
Example 3 - सत्यापित करें कि क्या $X(t)= \sin \omega t$ एक अजीब संकेत या एक भी संकेत है।
Solution - दिया $X(t) = \sin \omega t$
समय से उलट, हम प्राप्त करेंगे $\sin (-\omega t)$
लेकिन हम जानते हैं कि $\sin(-\phi) = -\sin \phi$।
इसलिए,
$$\sin (-\omega t) = -\sin \omega t$$यह सिग्नल के विषम होने की स्थिति को संतुष्ट करता है। इसलिए,$\sin \omega t$ एक अजीब संकेत है।
कंटीन्यू टाइम सिग्नल की तरह, डिसक्रीट टाइम सिग्नल को सिग्नल पर स्थितियां या संचालन के अनुसार वर्गीकृत किया जा सकता है।
यहां तक कि और विषम संकेत
यहां तक कि सिग्नल भी
एक संकेत को सममित या सममित कहा जाता है यदि यह निम्नलिखित स्थिति को संतुष्ट करता है;
$$x(-n) = x(n)$$
यहाँ, हम देख सकते हैं कि x (-1) = x (1), x (-2) = x (2) और x (-n) = x (n)। इस प्रकार, यह एक भी संकेत है।
अजीब संकेत
एक संकेत को विषम कहा जाता है यदि यह निम्नलिखित स्थिति को संतुष्ट करता है;
$$x(-n) = -x(n)$$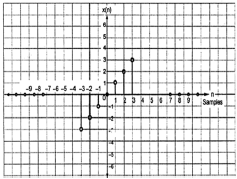
आकृति से, हम देख सकते हैं कि x (1) = -x (-1), x (2) = -x (2) और x (n) = -x (-n)। इसलिए, यह एक विषम और साथ ही एंटी-सममित संकेत है।
आवधिक और गैर-आवधिक संकेत
असतत समय संकेत आवधिक है और केवल अगर यह निम्न स्थिति को संतुष्ट करता है -
$$x(n+N) = x(n)$$यहाँ, x (n) सिग्नल N अवधि के बाद खुद को दोहराता है। यह एक कोसाइन सिग्नल पर विचार करके सबसे अच्छा समझा जा सकता है -
$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$संकेत के लिए आवधिक बनने के लिए, निम्नलिखित स्थिति को संतुष्ट किया जाना चाहिए;
$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$अर्थात $2\pi f_{0}N$ का एक अभिन्न गुण है $2\pi$
$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$असतत साइनसोइडल संकेतों की आवृत्तियों को अभिन्न एकाधिक द्वारा अलग किया जाता है $2\pi$।
ऊर्जा और पावर सिग्नल
ऊर्जा संकेत
असतत समय संकेत की ऊर्जा को ई। गणितीय रूप में निरूपित किया जाता है, इसे इस प्रकार लिखा जा सकता है;
$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$यदि प्रत्येक व्यक्ति का मान $x(n)$जोड़ा और जोड़ा जाता है, हम ऊर्जा संकेत प्राप्त करते हैं। यहाँ$x(n)$ ऊर्जा संकेत है और इसकी ऊर्जा समय के साथ परिमित होती है अर्थात $ 0 <E <\ infty $
पावर सिग्नल
असतत संकेत की औसत शक्ति को पी। गणितीय रूप में दर्शाया जाता है, इसे इस प्रकार लिखा जा सकता है;
$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$यहाँ, शक्ति परिमित है अर्थात 0 <P <ite। हालांकि, कुछ संकेत हैं, जो न तो ऊर्जा और न ही बिजली प्रकार के संकेत से संबंधित हैं।
अन्य संकेत हैं, जो उन पर किए गए ऑपरेशन का परिणाम हैं। कुछ सामान्य प्रकार के संकेतों की चर्चा नीचे की गई है।
संयुग्म संकेत
सिग्नल, जो स्थिति को संतुष्ट करता है $x(t) = x*(-t)$ संयुग्म संकेत कहलाते हैं।
लश्कर $x(t) = a(t)+jb(t)$... eqn। 1
इसलिए, $x(-t) = a(-t)+jb(-t)$
तथा $x*(-t) = a(-t)-jb(-t)$... eqn। 2
शर्त से, $x(t) = x*(-t)$
यदि हम व्युत्पन्न समीकरण 1 और 2 दोनों की तुलना करते हैं, तो हम देख सकते हैं कि वास्तविक भाग सम है, जबकि काल्पनिक भाग विषम है। यह संकेत के लिए एक संयुग्मित प्रकार होने की स्थिति है।
Conjugate एंटी-सिमेट्रिक सिग्नल
सिग्नल, जो स्थिति को संतुष्ट करते हैं $x(t) = -x*(-t)$ संयुग्म विरोधी सिमेट्रिक संकेत कहलाते हैं
लश्कर $x(t) = a(t)+jb(t)$... eqn। 1
इसलिए $x(-t) = a(-t)+jb(-t)$
तथा $x*(-t) = a(-t)-jb(-t)$
$-x*(-t) = -a(-t)+jb(-t)$... eqn। 2
दशा से $x(t) = -x*(-t)$
अब, फिर से तुलना करें, दोनों समीकरण उसी तरह जैसे हमने संकेतों को संयुग्मित करने के लिए किया था। यहां, हम पाएंगे कि वास्तविक भाग विषम है और काल्पनिक भाग सम है। यह एक संकेत के लिए संयुग्म विरोधी सममित प्रकार बनने की स्थिति है।
उदाहरण
संकेत दिया जाए $x(t) = \sin t+jt^{2}$।
यहाँ, असली हिस्सा है $\sin t$ विचित्र और काल्पनिक हिस्सा है $t^2$सम है। तो, इस संकेत को संयुग्म-विरोधी सममित संकेत के रूप में वर्गीकृत किया जा सकता है।
किसी भी फ़ंक्शन को दो भागों में विभाजित किया जा सकता है। एक हिस्सा कॉन्जुगेट सिमेट्री और दूसरा हिस्सा कंज्यूमिंग एंटी-सिमेट्रिक है। तो किसी भी संकेत x (t) के रूप में लिखा जा सकता है
$$x(t) = xcs(t)+xcas(t)$$कहाँ पे $xcs(t)$ सममित संकेत है और $xcas(t)$ संयुग्मन विरोधी सममित संकेत है
$$xcs(t) = \frac{[x(t)+x*(-t)]}{2}$$तथा
$$xcas(t) = \frac{[x(t)-x*(-t)]}{2}$$हाफ वेव सिमेट्रिक सिग्नल
जब कोई संकेत स्थिति को संतुष्ट करता है $cx(t) = -x(t\pm (\frac{T_{0}}{2}))$, इसे आधा लहर सममित संकेत कहा जाता है। यहां, सिग्नल के आयाम उलट और समय की शिफ्टिंग आधे समय तक होती है। आधा लहर सममित संकेत के लिए, औसत मूल्य शून्य होगा लेकिन स्थिति उलट होने पर ऐसा नहीं होता है।
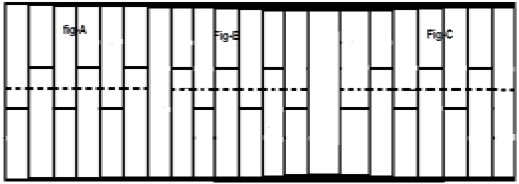
एक संकेत एक्स (टी) पर विचार करें जैसा कि ऊपर ए में दिखाया गया है। पहला कदम सिग्नल को शिफ्ट करना और बनाना है$x[t-(\frac{T}{2})]$। इसलिए, नया संकेत बदल जाता है जैसा कि आंकड़ा बी में दिखाया गया है। हम सिग्नल के आयाम को उल्टा करते हैं, अर्थात बनाते हैं$-x[t-(\frac{T}{2})]$ जैसा कि आकृति सी में दिखाया गया है। चूंकि, यह संकेत आधे समय की शिफ्टिंग और आयाम के उत्क्रमण के बाद खुद को दोहराता है, यह एक आधा लहर सममित संकेत है।
ऑर्थोगोनल सिग्नल
दो संकेतों x (t) और y (t) को ऑर्थोगोनल कहा जाता है यदि वे निम्नलिखित दो स्थितियों को पूरा करते हैं।
Condition 1 - $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [गैर-आवधिक संकेत के लिए]
Condition 2 - $\int x(t)y(t) = 0$ [समय-समय पर संकेत के लिए]
सिग्नल, जिसमें विषम हार्मोनिक्स (3 आरडी , 5 वें , 7 वें ... आदि) हैं और अलग-अलग आवृत्तियां हैं, एक-दूसरे के लिए पारस्परिक रूप से ऑर्थोगोनल हैं।
त्रिकोणमितीय प्रकार के संकेतों में, साइन फ़ंक्शंस और कोज़ाइन फ़ंक्शंस एक-दूसरे के लिए ऑर्थोगोनल भी हैं; बशर्ते, उनकी एक ही आवृत्ति हो और एक ही चरण में हों। इसी तरह से डीसी (डायरेक्ट करंट सिग्नल) और साइनसॉइडल सिग्नल भी एक-दूसरे के लिए ऑर्थोगोनल हैं। यदि x (t) और y (t) दो ऑर्थोगोनल सिग्नल हैं और$z(t) = x(t)+y(t)$ तब z (t) की शक्ति और ऊर्जा के रूप में लिखा जा सकता है;
$$P(z) = p(x)+p(y)$$ $$E(z) = E(x)+E(y)$$उदाहरण
संकेत का विश्लेषण करें: $z(t) = 3+4\sin(2\pi t+30^0)$
यहाँ, संकेत में DC संकेत (3) और एक साइन फ़ंक्शन शामिल हैं। इसलिए, संपत्ति द्वारा यह संकेत एक ऑर्थोगोनल सिग्नल है और इसमें दो उप-सिग्नल एक दूसरे से पारस्परिक रूप से ऑर्थोगोनल हैं।
शिफ्टिंग का अर्थ है सिग्नल की गति, या तो समय डोमेन (Y- अक्ष के आसपास) या आयाम डोमेन (X- अक्ष के आसपास) में। तदनुसार, हम शिफ्टिंग को दो श्रेणियों में वर्गीकृत कर सकते हैं, जिन्हें टाइम शिफ्टिंग और एम्प्लिट्यूड शिफ्टिंग के नाम से जाना जाता है, इन पर बाद में नीचे चर्चा की गई।
समय बदलता है
टाइम शिफ्टिंग का मतलब है, टाइम डोमेन में सिग्नल शिफ्ट करना। गणितीय रूप से, इसे लिखा जा सकता है
$$x(t) \rightarrow y(t+k)$$यह K मान धनात्मक हो सकता है या यह ऋणात्मक हो सकता है। K मान के संकेत के अनुसार, हमारे पास दो प्रकार की शिफ्टिंग है, जिसका नाम राइट शिफ्टिंग और लेफ्ट शिफ्टिंग है।
केस 1 (K> 0)
जब K शून्य से अधिक होता है, तो सिग्नल का स्थानांतरण समय डोमेन में "बाएं" की ओर होता है। इसलिए, इस प्रकार की शिफ्टिंग को सिग्नल के लेफ्ट शिफ्टिंग के रूप में जाना जाता है।
Example
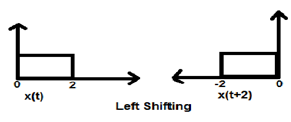
केस 2 (K <0)
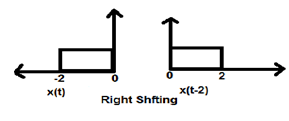
जब K शून्य से कम होता है तो सिग्नल की शिफ्टिंग टाइम डोमेन में दाईं ओर होती है। इसलिए, इस प्रकार की शिफ्टिंग को राइट शिफ्टिंग के रूप में जाना जाता है।
Example
नीचे दिया गया आंकड़ा 2 द्वारा सिग्नल के सही स्थानांतरण को दर्शाता है।
आयाम शिफ्टिंग
आयाम शिफ्टिंग का अर्थ है आयाम डोमेन में सिग्नल का स्थानांतरण (एक्स-एक्सिस के आसपास)। गणितीय रूप से, इसका प्रतिनिधित्व इस प्रकार किया जा सकता है -
$$x(t) \rightarrow x(t)+K$$यह K मान धनात्मक या ऋणात्मक हो सकता है। तदनुसार, हमारे पास दो प्रकार के आयाम हैं जो बाद में नीचे चर्चा किए गए हैं।
केस 1 (K> 0)
जब K शून्य से अधिक होता है, तो सिग्नल का स्थानांतरण एक्स-अक्ष में ऊपर की ओर होता है। इसलिए, इस प्रकार के स्थानांतरण को ऊपर की ओर स्थानांतरण के रूप में जाना जाता है।
Example
आइए एक संकेत x (t) पर विचार करें जो कि दिया गया है;
$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$हमने K = + 1 लिया है, इसलिए नए संकेत के रूप में लिखा जा सकता है -
$y(t) \rightarrow x(t)+1$ तो, वाई (टी) के रूप में अंत में लिखा जा सकता है;
$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$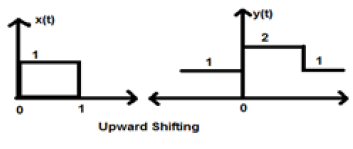
केस 2 (K <0)
जब K शून्य से कम होता है तो सिग्नल का स्थानांतरण X- अक्ष में नीचे की ओर होता है। इसलिए, इसे सिग्नल की डाउनवर्ड शिफ्टिंग कहा जाता है।
Example
आइए एक संकेत x (t) पर विचार करें जो कि दिया गया है;
$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$हमने K = -1 लिया है, इसलिए नए संकेत के रूप में लिखा जा सकता है;
$y(t)\rightarrow x(t)-1$ तो, वाई (टी) के रूप में अंत में लिखा जा सकता है;
$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$
सिग्नल के स्केलिंग का मतलब है, एक स्थिर सिग्नल के समय या आयाम के साथ गुणा किया जाता है।
टाइम स्केलिंग
यदि किसी स्थिरांक को समय अक्ष से गुणा किया जाता है तो उसे टाइम स्केलिंग के रूप में जाना जाता है। इसे गणितीय रूप में दर्शाया जा सकता है;
$x(t) \rightarrow y(t) = x(\alpha t)$ या $x(\frac{t}{\alpha})$; जहां α ≠ 0
तो y- अक्ष समान होने के नाते, x- अक्ष परिमाण घटता है या स्थिर (चाहे सकारात्मक या नकारात्मक) संकेत के अनुसार बढ़ता है। इसलिए, स्केलिंग को भी दो श्रेणियों में विभाजित किया जा सकता है जैसा कि नीचे चर्चा की गई है।
समय संपीड़न
जब भी अल्फा शून्य से अधिक होता है, सिग्नल का आयाम अल्फा से विभाजित हो जाता है जबकि Y- अक्ष का मान समान रहता है। इसे टाइम कम्प्रेशन के नाम से जाना जाता है।
Example
आइए एक संकेत x (t) पर विचार करें, जो नीचे दिए गए चित्र में दिखाया गया है। आइए हम अल्फा के मान को 2 के रूप में लेते हैं। इसलिए, y (t) x (2t) होगा, जो कि दिए गए चित्र में दर्शाया गया है।

स्पष्ट रूप से, हम उपरोक्त आंकड़ों से देख सकते हैं कि y- अक्ष में समय परिमाण समान है लेकिन x- अक्ष में आयाम 4 से घटकर 2 हो जाता है। इसलिए, यह समय संपीड़न का मामला है।
समय विस्तार
जब समय को निरंतर अल्फा द्वारा विभाजित किया जाता है, तो संकेत के वाई-अक्ष परिमाण को एक्स-अक्ष परिमाण रखते हुए, अल्फा बार गुणा किया जाता है। इसलिए, इसे टाइम एक्सपेंशन टाइप सिग्नल कहा जाता है।
Example
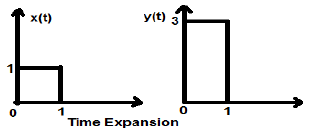
आइए एक वर्ग संकेत x (t) पर विचार करें, परिमाण 1. जब हम समय को लगातार 3 से घटाते हैं, तो ऐसा $x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$, फिर सिग्नल के आयाम को 3 गुना संशोधित किया जाता है जो नीचे दिए गए आंकड़े में दिखाया गया है।
आयाम स्केलिंग
सिग्नल के आयाम के साथ एक स्थिरांक का गुणा आयाम स्केलिंग का कारण बनता है। स्थिरांक के संकेत के आधार पर, यह या तो आयाम स्केलिंग या क्षीणन हो सकता है। आइए एक वर्ग तरंग संकेत x (t) = t (t / 4) पर विचार करें।
मान लीजिए कि हम एक और फ़ंक्शन y (t) = 2 t (t / 4) परिभाषित करते हैं। इस स्थिति में, y- अक्ष का मान दोगुना हो जाएगा, समय के अक्ष का मान रखते हुए। नीचे दिए गए आंकड़े में सचित्र है।
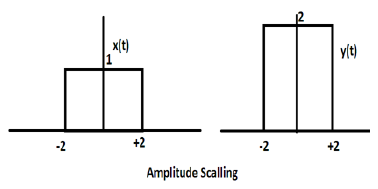
Z (t) के रूप में परिभाषित एक और वर्ग तरंग फ़ंक्शन पर विचार करें जहाँ z (t) = 0.5 Consider (t / 4)। यहां, फ़ंक्शन z (t) का आयाम x (t) का आधा होगा अर्थात समय अक्ष एक ही शेष रहेगा, आयाम अक्ष को आधा किया जाएगा। यह नीचे दिए गए आंकड़े से दर्शाया गया है।
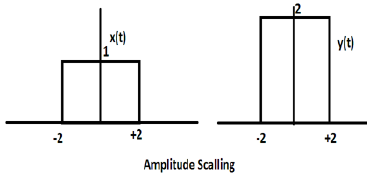
जब भी किसी सिग्नल में समय -1 से गुणा हो जाता है, तो सिग्नल उलट हो जाता है। यह Y या X- अक्ष के बारे में अपनी दर्पण छवि का निर्माण करता है। इसे सिग्नल के रिवर्सल के रूप में जाना जाता है।
रिवर्सल को इस स्थिति के आधार पर दो प्रकारों में वर्गीकृत किया जा सकता है कि क्या संकेत के समय या आयाम को 1 से गुणा किया जाता है।
समय उलटा
जब भी सिग्नल के समय को 1 से गुणा किया जाता है, तो इसे सिग्नल के समय उलट के रूप में जाना जाता है। इस मामले में, संकेत वाई-अक्ष के बारे में अपनी दर्पण छवि का उत्पादन करता है। गणितीय रूप से, इसे इस प्रकार लिखा जा सकता है;
$$x(t) \rightarrow y(t) \rightarrow x(-t)$$इसे निम्नलिखित उदाहरण से सबसे अच्छा समझा जा सकता है।

उपरोक्त उदाहरण में, हम स्पष्ट रूप से देख सकते हैं कि सिग्नल को इसके वाई-अक्ष के बारे में उलट दिया गया है। तो, यह एक प्रकार का समय स्केलिंग भी है, लेकिन यहां स्केलिंग मात्रा हमेशा (-1) होती है।
आयाम उलटा
जब भी किसी सिग्नल के आयाम को 1 से गुणा किया जाता है, तो इसे आयाम उलट के रूप में जाना जाता है। इस स्थिति में, संकेत एक्स-अक्ष के बारे में अपनी दर्पण छवि का उत्पादन करता है। गणितीय रूप से, इसे इस प्रकार लिखा जा सकता है;
$$x(t)\rightarrow y(t)\rightarrow -x(t)$$निम्नलिखित उदाहरण पर विचार करें। आयाम उलट स्पष्ट रूप से देखा जा सकता है।
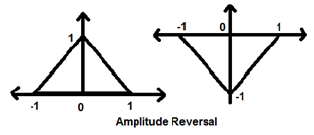
संकेतों पर किए गए दो बहुत ही महत्वपूर्ण संचालन विभेदीकरण और एकीकरण हैं।
भेदभाव
किसी भी सिग्नल x (t) का विभेदन का अर्थ है समय के संबंध में उस सिग्नल का ढलान प्रतिनिधित्व। गणितीय रूप से, इसे इस रूप में दर्शाया गया है;
$$x(t)\rightarrow \frac{dx(t)}{dt}$$OPAMP भेदभाव के मामले में, यह कार्यप्रणाली बहुत मददगार है। हम सूत्र का उपयोग करने के बजाय आसानी से एक संकेत को रेखांकन में अंतर कर सकते हैं। हालांकि, शर्त यह है कि संकेत या तो आयताकार या त्रिकोणीय प्रकार का होना चाहिए, जो ज्यादातर मामलों में होता है।
| मूल संकेत | विभेदित संकेत |
|---|---|
| बढ़ाना | कदम |
| कदम | आवेग |
| आवेग | 1 |
उपरोक्त तालिका विभेदित होने के बाद संकेत की स्थिति को दर्शाती है। उदाहरण के लिए, एक रैंप सिग्नल विभेदन के बाद एक स्टेप सिग्नल में परिवर्तित हो जाता है। इसी तरह, एक इकाई चरण संकेत एक आवेग संकेत बन जाता है।
उदाहरण
संकेत हमें दिया जाए $x(t) = 4[r(t)-r(t-2)]$। जब यह संकेत दिया जाता है, तो यह नीचे दी गई आकृति के बाईं ओर एक जैसा दिखेगा। अब, हमारा उद्देश्य दिए गए संकेत को अलग करना है।
शुरू करने के लिए, हम दिए गए समीकरण को अलग करना शुरू करेंगे। हम जानते हैं कि भेदभाव के बाद रैंप सिग्नल यूनिट स्टेप सिग्नल देता है।
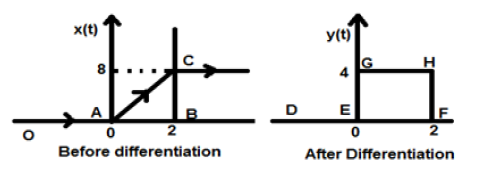
तो हमारे परिणामस्वरूप संकेत y (t) के रूप में लिखा जा सकता है;
$y(t) = \frac{dx(t)}{dt}$
$= \frac{d4[r(t)-r(t-2)]}{dt}$
$= 4[u(t)-u(t-2)]$
अब इस सिग्नल को अंत में प्लॉट किया गया है, जो कि ऊपर के आंकड़े के दाहिने हाथ में दिखाया गया है।
किसी भी सिग्नल के एकीकरण का मतलब है कि संशोधित सिग्नल प्राप्त करने के लिए विशेष समय डोमेन के तहत उस सिग्नल का योग। गणितीय रूप से, इसे इस रूप में दर्शाया जा सकता है -
$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$यहां भी, ज्यादातर मामलों में हम गणितीय एकीकरण कर सकते हैं और परिणामी संकेत प्राप्त कर सकते हैं लेकिन त्वरित उत्तराधिकार में प्रत्यक्ष एकीकरण उन संकेतों के लिए संभव है जो आयताकार प्रारूप में चित्रित किए गए हैं। भेदभाव की तरह, यहां भी, हम परिणाम प्राप्त करने के लिए एक तालिका का उल्लेख करेंगे।
| मूल संकेत | एकीकृत संकेत |
|---|---|
| 1 | आवेग |
| आवेग | कदम |
| कदम | बढ़ाना |
उदाहरण
आइए हम एक संकेत पर विचार करें $x(t) = u(t)-u(t-3)$। इसे नीचे चित्र -1 में दिखाया गया है। स्पष्ट रूप से, हम देख सकते हैं कि यह एक कदम संकेत है। अब हम इसे एकीकृत करेंगे। तालिका का उल्लेख करते हुए, हम जानते हैं कि स्टेप सिग्नल के एकीकरण से रैंप सिग्नल की पैदावार होती है।
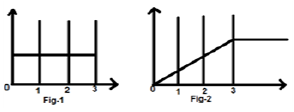
हालाँकि, हम गणितीय रूप से इसकी गणना करेंगे,
$y(t) = \int_{-\infty}^{t}x(t)dt$
$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$
$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$
$= r(t)-r(t-3)$
जैसा कि अंजीर -2 में दिखाया गया है,
टाइम डोमेन में दो सिग्नलों का कनवल्शन फ़्रीक्वेंसी डोमेन में उनके प्रतिनिधित्व के गुणन के बराबर है। गणितीय रूप से, हम दो संकेतों के दृढ़ संकल्प को लिख सकते हैं
$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$दृढ़ संकल्प के लिए कदम
- संकेत x 1 (t) लें और t = p को वहां रखें ताकि वह x 1 (p) हो जाए।
- सिग्नल x 2 (t) लें और चरण 1 करें और इसे x 2 (p) करें।
- सिग्नल को फोल्ड करना यानी x 2 (-p)।
- उपरोक्त संकेत x 2 [- (pt)] की शिफ्टिंग समय पर करें
- फिर दोनों संकेतों का गुणा करें। अर्थात$x_{1}(p).x_{2}[−(p−t)]$
उदाहरण
आइए हम एक स्टेप सिग्नल u (t) का कनवल्शन अपनी तरह से करें।
$y(t) = u(t)*u(t)$
$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$
अब यह टी शून्य से अधिक या कम हो सकती है, जो नीचे दिए गए आंकड़ों में दिखाई गई हैं
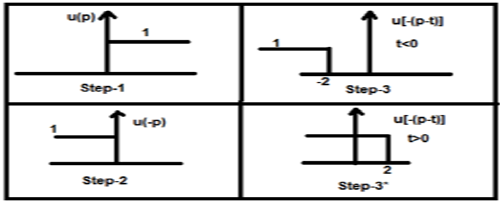
तो, उपरोक्त मामले के साथ, परिणाम निम्न संभावनाओं के साथ उत्पन्न होता है
$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$
$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$
बातचीत के गुण
विनिमेय
इसमें कहा गया है कि सजा का आदेश कोई मायने नहीं रखता है, जिसे गणितीय रूप से दिखाया जा सकता है
$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$जोड़नेवाला
इसमें कहा गया है कि तीन संकेतों को शामिल करते हुए सजा का आदेश कुछ भी हो सकता है। गणितीय रूप से, इसे इस रूप में दिखाया जा सकता है;
$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$विभाजित करनेवाला
दो संकेतों को पहले जोड़ा जा सकता है, और फिर उनके संकेत को तीसरे संकेत के लिए बनाया जा सकता है। यह तीसरे संकेत के साथ व्यक्तिगत रूप से दो संकेतों के दृढ़ीकरण के बराबर है और अंत में जोड़ा गया है। गणितीय रूप से, इसे इस प्रकार लिखा जा सकता है;
$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$क्षेत्र
यदि एक संकेत दो संकेतों के दृढ़ीकरण का परिणाम है तो संकेत का क्षेत्र उन व्यक्तिगत संकेतों का गुणन है। गणितीय रूप से यह लिखा जा सकता है
अगर $y(t) = x_{1}*x_{2}(t)$
फिर, y का क्षेत्रफल (t) = x 1 का क्षेत्रफल (t) x 2 का क्षेत्रफल (t)
स्केलिंग
यदि दो संकेतों को कुछ अज्ञात निरंतर "और" के लिए स्केल किया जाता है, तो परिणामी संकेत भी उसी निरंतर "ए" के लिए दृढ़ हो जाएगा और उस मात्रा से विभाजित किया जाएगा जैसा कि नीचे दिखाया गया है।
अगर, $x_{1}(t)*x_{2}(t) = y(t)$
फिर, $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$
विलंब
मान लीजिए कि एक संकेत y (t) दो संकेतों X1 (t) और x2 (t) के दृढ़ संकल्प का परिणाम है। यदि दो संकेतों को क्रमशः समय t1 और t2 द्वारा विलंबित किया जाता है, तो परिणामी संकेत y (t) देरी से (t1 + t2) होगा। गणितीय रूप से, इसे इस प्रकार लिखा जा सकता है -
अगर, $x_{1}(t)*x_{2}(t) = y(t)$
फिर, $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$
हल के उदाहरण
Example 1 - संकेतों u (t-1) और u (t-2) के दृढ़ संकल्प का पता लगाएं।
Solution- दिए गए संकेत यू (टी -1) और यू (टी -2) हैं। उनका कनविक्शन नीचे दिखाए अनुसार किया जा सकता है -
$y(t) = u(t-1)*u(t-2)$
$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$
$= r(t-1)+r(t-2)$
$= r(t-3)$
Example 2 - दिए गए दो संकेतों के दृढ़ संकल्प का पता लगाएं
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$
Solution -
x 2 (n) के रूप में डिकोड किया जा सकता है$x_{2}(n) = \lbrace 2,2,2,2,2\rbrace Originalfirst$
x 1 (n) पहले दिया गया है$= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$
इसी तरह, $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
परिणामी संकेत,
$X(Z) = X_{1}(Z)X_{2}(z)$
$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$
उपरोक्त के Z- परिवर्तन को उलटते हुए, हमें परिणामी संकेत मिलेगा
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ पहले की उत्पत्ति
Example 3 - निम्नलिखित 2 संकेतों के दृढ़ संकल्प का निर्धारण करें -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
संकेतों के जेड-परिवर्तन को लेते हुए, हम प्राप्त करते हैं,
$x(z) = 2+2Z^{-1}+2Z^{-3}$
तथा $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$
अब दो सिग्नल के दोषी होने का मतलब है उनके जेड-ट्रांसफॉर्मेशन का गुणा
अर्थात् $Y(Z) = X(Z) \times h(Z)$
$= \lbrace 2+2Z^{-1}+2Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$
$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+3Z^{-5}+Z^{-6}\rbrace$
उलटा Z- परिवर्तन लेते हुए, परिणामी संकेत के रूप में लिखा जा सकता है;
$y(n) = \lbrace 2,5,8,6,6,1 \rbrace Originalfirst$
कुछ सिस्टम में फीडबैक है और कुछ में नहीं है। जिनके पास फीडबैक सिस्टम नहीं है, उनका आउटपुट केवल इनपुट के वर्तमान मूल्यों पर निर्भर करता है। उस समय डेटा का पिछला मान मौजूद नहीं है। इस प्रकार के सिस्टम को स्टैटिक सिस्टम के रूप में जाना जाता है। यह भविष्य के मूल्यों पर भी निर्भर नहीं करता है।
चूंकि इन प्रणालियों का कोई पिछला रिकॉर्ड नहीं है, इसलिए उनके पास कोई मेमोरी भी नहीं है। इसलिए, हम कहते हैं कि सभी स्टैटिक सिस्टम मेमोरी-कम सिस्टम हैं। आइए हम इस अवधारणा को बेहतर तरीके से समझने के लिए एक उदाहरण लें।
उदाहरण
आइए हम सत्यापित करें कि निम्नलिखित सिस्टम स्थिर सिस्टम हैं या नहीं।
- $y(t) = x(t)+x(t-1)$
- $y(t) = x(2t)$
- $y(t) = x = \sin [x(t)]$
ए) $y(t) = x(t)+x(t-1)$
यहाँ, x (t) वर्तमान मान है। इसका उस समय के पुराने मूल्यों से कोई संबंध नहीं है। तो, यह एक स्थिर प्रणाली है। हालाँकि, x (t-1) के मामले में, यदि हम t = 0 डालते हैं, तो यह x (-1) तक कम हो जाएगा जो कि पिछले मान पर निर्भर है। तो, यह स्थिर नहीं है। इसलिए यहाँ y (t) एक स्थिर प्रणाली नहीं है।
ख) $y(t) = x(2t)$
यदि हम t = 2 को प्रतिस्थापित करते हैं, तो परिणाम y (t) = x (4) होगा। फिर, यह भविष्य के मूल्य पर निर्भर है। तो, यह भी एक स्थिर प्रणाली नहीं है।
सी) $y(t) = x = \sin [x(t)]$
इस अभिव्यक्ति में, हम साइन फ़ंक्शन के साथ काम कर रहे हैं। साइन फंक्शन की सीमा -1 से +1 के बीच होती है। इसलिए, x (t) के लिए हम जो भी मान लेते हैं, वह -1 से +1 के बीच में मिलेगा। इसलिए, हम कह सकते हैं कि यह किसी भी अतीत या भविष्य के मूल्यों पर निर्भर नहीं है। इसलिए, यह एक स्थिर प्रणाली है।
उपरोक्त उदाहरणों से, हम निम्नलिखित निष्कर्ष निकाल सकते हैं -
- किसी भी समय शिफ्टिंग प्रणाली स्थिर नहीं है।
- आयाम शिफ्टिंग वाली कोई भी प्रणाली भी स्थिर नहीं है।
- एकीकरण और भेदभाव के मामले भी स्थिर नहीं हैं।
यदि कोई प्रणाली उस समय के किसी भी समय सिग्नल के अतीत और भविष्य के मूल्य पर निर्भर करती है तो इसे डायनामिक सिस्टम के रूप में जाना जाता है। स्टैटिक सिस्टम के विपरीत, ये मेमोरी कम सिस्टम नहीं हैं। वे अतीत और भविष्य के मूल्यों को संग्रहीत करते हैं। इसलिए, उन्हें कुछ मेमोरी की आवश्यकता होती है। आइए इस सिद्धांत को कुछ उदाहरणों के माध्यम से बेहतर ढंग से समझते हैं।
उदाहरण
पता लगाएँ कि क्या निम्न प्रणालियाँ गतिशील हैं।
a) $y(t) = x(t+1)$
इस मामले में यदि हम समीकरण में t = 1 डालते हैं, तो इसे x (2) में बदल दिया जाएगा, जो कि भविष्य पर निर्भर मूल्य है। क्योंकि यहाँ हम 1 के रूप में इनपुट दे रहे हैं लेकिन यह x (2) के लिए मान दिखा रहा है। चूंकि यह भविष्य पर निर्भर संकेत है, इसलिए स्पष्ट रूप से यह एक गतिशील प्रणाली है।
b) $y(t) = Real[x(t)]$
$$= \frac{[x(t)+x(t)^*]}{2}$$इस मामले में, हम जो भी मूल्य डालेंगे वह उस समय वास्तविक मूल्य संकेत दिखाएगा। इसका भविष्य या अतीत के मूल्यों पर कोई निर्भरता नहीं है। इसलिए, यह एक गतिशील प्रणाली नहीं है, बल्कि यह एक स्थिर प्रणाली है।
c) $y(t) = Even[x(t)]$
$$= \frac{[x(t)+x(-t)]}{2}$$यहां, यदि हम t = 1 को स्थानापन्न करेंगे, तो एक संकेत x (1) दिखाता है और दूसरा x (-1) दिखाएगा जो कि एक अतीत मान है। इसी तरह, अगर हम t = -1 डालेंगे तो एक सिग्नल x (-1) और दूसरा x (1) दिखाएगा जो कि भविष्य का मान है। इसलिए, स्पष्ट रूप से यह गतिशील प्रणाली का मामला है।
d) $y(t) = \cos [x(t)]$
इस मामले में, जैसा कि सिस्टम कॉशन फ़ंक्शन है, इसमें मूल्यों का एक निश्चित डोमेन है जो -1 से +1 के बीच स्थित है। इसलिए, हम जो भी मूल्य डालेंगे, उसका परिणाम हमें निर्दिष्ट सीमा के भीतर मिलेगा। इसलिए, यह एक स्थिर प्रणाली है
उपरोक्त उदाहरणों से, हम निम्नलिखित निष्कर्ष निकाल सकते हैं -
- हर समय शिफ्टिंग केस सिग्नल डायनेमिक सिग्नल होते हैं।
- समय स्केलिंग के मामले में भी, सभी सिग्नल गतिशील सिग्नल हैं।
- एकीकरण मामलों के संकेत गतिशील संकेत हैं।
पहले, हमने देखा कि सिस्टम को स्थिर होने के लिए भविष्य और पिछले मूल्यों से स्वतंत्र होने की आवश्यकता है। इस मामले में, हालत थोड़ा संशोधन के साथ लगभग समान है। यहां, सिस्टम को कार्य-कारण होने के लिए, इसे केवल भविष्य के मूल्यों से स्वतंत्र होना चाहिए। इसका मतलब है कि पिछली निर्भरता प्रणाली के लिए कोई कारण नहीं बनेगी क्योंकि यह कारण बन सकती है।
व्यावहारिक या व्यावहारिक रूप से वास्तविक प्रणाली हैं। आइए इसे बेहतर समझने के लिए कुछ उदाहरणों पर विचार करें।
उदाहरण
आइए हम निम्नलिखित संकेतों पर विचार करें।
a) $y(t) = x(t)$
यहाँ, संकेत केवल x के वर्तमान मूल्यों पर निर्भर है। उदाहरण के लिए यदि हम t = 3 को प्रतिस्थापित करते हैं, तो परिणाम केवल उस समय के लिए दिखाई देगा। इसलिए, चूंकि भविष्य के मूल्य पर इसकी कोई निर्भरता नहीं है, इसलिए हम इसे कॉसल सिस्टम कह सकते हैं।
b) $y(t) = x(t-1)$
यहां, सिस्टम पिछले मानों पर निर्भर करता है। उदाहरण के लिए यदि हम t = 3 को प्रतिस्थापित करते हैं, तो अभिव्यक्ति x (2) तक कम हो जाएगी, जो कि हमारे इनपुट के खिलाफ एक पिछले मूल्य है। उदाहरण के लिए, यह भविष्य के मूल्यों पर निर्भर करता है। इसलिए, यह प्रणाली भी एक कारण प्रणाली है।
c) $y(t) = x(t)+x(t+1)$
इस मामले में, सिस्टम के दो भाग हैं। भाग एक्स (टी), जैसा कि हमने पहले चर्चा की है, केवल वर्तमान मूल्यों पर निर्भर करता है। इसलिए, इसके साथ कोई मुद्दा नहीं है। हालाँकि, यदि हम x (t + 1) के मामले को लेते हैं, तो यह स्पष्ट रूप से भविष्य के मूल्यों पर निर्भर करता है क्योंकि यदि हम t = 1 डालते हैं, तो अभिव्यक्ति x (2) तक कम हो जाएगी, जो कि भविष्य का मूल्य है। इसलिए, यह कारण नहीं है।
एक गैर-कारण प्रणाली, कार्य-प्रणाली के ठीक विपरीत है। यदि कोई सिस्टम किसी भी समय इनपुट के भविष्य के मूल्यों पर निर्भर करता है, तो सिस्टम को गैर-कारण प्रणाली कहा जाता है।
उदाहरण
आइए हम कुछ उदाहरण लेते हैं और इसे बेहतर तरीके से समझने की कोशिश करते हैं।
a) $y(t) = x(t+1)$
इस प्रणाली की चर्चा हम पहले ही कर चुके हैं। किसी भी इनपुट के लिए, यह सिस्टम को उसके भविष्य के मूल्य तक कम कर देगा। उदाहरण के लिए, यदि हम t = 2 रखते हैं, तो यह x (3) तक कम हो जाएगा, जो कि भविष्य का मूल्य है। इसलिए, सिस्टम गैर-कारण है।
b) $y(t) = x(t)+x(t+2)$
इस स्थिति में, x (t) विशुद्ध रूप से एक वर्तमान मूल्य पर निर्भर कार्य है। हमने पहले ही चर्चा की है कि x (t + 2) फ़ंक्शन भविष्य पर निर्भर है क्योंकि t = 3 के लिए यह x (5) के लिए मान देगा। इसलिए, यह गैर-कारण है।
c) $y(t) = x(t-1)+x(t)$
इस प्रणाली में, यह दिए गए इनपुट के वर्तमान और पिछले मूल्यों पर निर्भर करता है। हम जो भी मूल्य प्रतिस्थापित करते हैं, वह कभी भी भविष्य की निर्भरता नहीं दिखाएगा। स्पष्ट रूप से, यह एक गैर-कारण प्रणाली नहीं है; बल्कि यह एक Causal प्रणाली है।
एक विरोधी-कारण प्रणाली एक गैर-कारण प्रणाली का केवल थोड़ा संशोधित संस्करण है। सिस्टम केवल इनपुट के भविष्य के मूल्यों पर निर्भर करता है। इसकी वर्तमान या पिछले मूल्यों पर कोई निर्भरता नहीं है।
उदाहरण
पता लगाएँ कि क्या निम्नलिखित सिस्टम विरोधी कारण हैं।
a) $y(t) = x(t)+x(t-1)$
सिस्टम के दो उप-कार्य हैं। एक उप फ़ंक्शन x (t + 1) इनपुट के भविष्य के मूल्य पर निर्भर करता है लेकिन एक अन्य उप-फ़ंक्शन x (t) केवल वर्तमान पर निर्भर करता है। जैसा कि सिस्टम भविष्य के मूल्य के अलावा वर्तमान मूल्य पर भी निर्भर है, यह प्रणाली विरोधी-कारण नहीं है।
b) $y(t) = x(t+3)$
यदि हम उपरोक्त सिस्टम का विश्लेषण करते हैं, तो हम देख सकते हैं कि सिस्टम केवल सिस्टम के भविष्य के मूल्यों पर निर्भर करता है, यदि हम t = 0 डालते हैं, तो यह x (3) तक कम हो जाएगा, जो कि भविष्य का मूल्य है। यह प्रणाली विरोधी-कारण प्रणाली का एक आदर्श उदाहरण है।
एक रेखीय प्रणाली सुपरपोजिशन के नियमों का पालन करती है। यह कानून व्यवस्था की रैखिकता को साबित करने के लिए आवश्यक और पर्याप्त स्थिति है। इसके अलावा, प्रणाली दो प्रकार के कानूनों का एक संयोजन है -
- संवेदनशीलता का नियम
- समरूपता का नियम

दोनों, समरूपता का कानून और नशे की लत के कानून को उपरोक्त आंकड़ों में दिखाया गया है। हालांकि, यह जांचने के लिए कुछ अन्य शर्तें हैं कि सिस्टम रैखिक है या नहीं।
The conditions are -
- शून्य इनपुट के लिए आउटपुट शून्य होना चाहिए।
- सिस्टम में कोई भी गैर-रेखीय ऑपरेटर मौजूद नहीं होना चाहिए।
गैर-रेखीय ऑपरेटरों के उदाहरण -
(ए) त्रिकोणमितीय ऑपरेटर- पाप, कॉस, टैन, कॉट, सेक, कोसेक आदि।
(b) घातांक, लघुगणक, मापांक, वर्ग, घन आदि।
(c) sa (i / p), Sinc (i / p), Sqn (i / p) आदि।
या तो इनपुट x या आउटपुट y में ये नॉन-लीनियर ऑपरेटर्स नहीं होने चाहिए।
उदाहरण
आइए जानें कि क्या निम्नलिखित प्रणालियां रैखिक हैं।
a) $y(t) = x(t)+3$
यह प्रणाली एक रैखिक प्रणाली नहीं है क्योंकि यह पहली शर्त का उल्लंघन करती है। यदि हम इनपुट को शून्य के रूप में रखते हैं, तो x (t) = 0 बनाते हैं, तो आउटपुट शून्य नहीं है।
b) $y(t) = \sin tx(t)$
इस प्रणाली में, यदि हम शून्य के रूप में इनपुट देते हैं, तो आउटपुट शून्य हो जाएगा। इसलिए, पहली शर्त स्पष्ट रूप से संतुष्ट है। फिर से, कोई गैर-रेखीय ऑपरेटर नहीं है जिसे x (t) पर लागू किया गया है। इसलिए, दूसरी शर्त भी संतुष्ट है। इसलिए, सिस्टम एक रैखिक प्रणाली है।
c) $y(t) = \sin (x(t))$
उपरोक्त प्रणाली में, पहली शर्त संतुष्ट है क्योंकि अगर हम x (t) = 0 डालते हैं, तो आउटपुट भी पाप होगा (0) = 0. हालांकि, दूसरी स्थिति संतुष्ट नहीं है, क्योंकि एक गैर-रेखीय ऑपरेटर है जो संचालित एक्स (टी)। इसलिए, सिस्टम रैखिक नहीं है।
यदि हम इस प्रणाली को परिभाषित करना चाहते हैं, तो हम कह सकते हैं कि सिस्टम, जो रैखिक नहीं हैं, गैर-रेखीय प्रणाली हैं। स्पष्ट रूप से, सभी स्थितियों, जिन्हें रैखिक प्रणालियों में उल्लंघन किया जा रहा है, को इस मामले में संतुष्ट होना चाहिए।
शर्तेँ
इनपुट लागू होने पर आउटपुट शून्य नहीं होना चाहिए।
किसी भी गैर-रेखीय ऑपरेटर को सिस्टम पर गैर-रैखिक बनाने के लिए इनपुट या आउटपुट पर लागू किया जा सकता है।
उदाहरण
यह पता लगाने के लिए कि दिए गए सिस्टम रैखिक या गैर-रैखिक हैं या नहीं।
a) $y(t) = e^{x(t)}$
उपरोक्त सिस्टम में, पहली शर्त संतुष्ट है क्योंकि अगर हम इनपुट को शून्य बनाते हैं, तो आउटपुट 1. है इसके अलावा, एक्सपोनेंशियल नॉन-लीनियर ऑपरेटर इनपुट पर लागू होता है। स्पष्ट रूप से, यह गैर-रैखिक प्रणाली का मामला है।
b) $y(t) = x(t+1)+x(t-1)$
उपरोक्त प्रकार की प्रणाली अतीत और भविष्य के मूल्यों से संबंधित है। हालाँकि, यदि हम इसके इनपुट को शून्य कर देंगे, तो इसका कोई भी मान मौजूद नहीं है। इसलिए, हम कह सकते हैं कि यदि इनपुट शून्य है, तो इनपुट की समय-सीमा और समय स्थानांतरित संस्करण भी शून्य होगा, जो हमारी पहली शर्त का उल्लंघन करता है। फिर से, कोई गैर-रेखीय ऑपरेटर मौजूद नहीं है। इसलिए, दूसरी शर्त का भी उल्लंघन किया जाता है। स्पष्ट रूप से, यह प्रणाली एक गैर-रेखीय प्रणाली नहीं है; बल्कि यह एक रैखिक प्रणाली है।
एक समय-अपरिवर्तनीय प्रणाली के लिए, आउटपुट और इनपुट को कुछ समय इकाई द्वारा विलंबित किया जाना चाहिए। इनपुट में प्रदान की गई किसी भी देरी को आउटपुट में एक समय अपरिवर्तनीय प्रणाली के लिए प्रतिबिंबित किया जाना चाहिए।
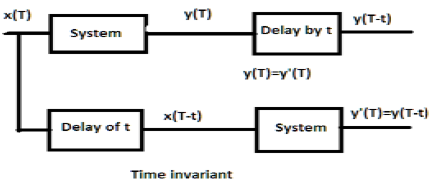
उदाहरण
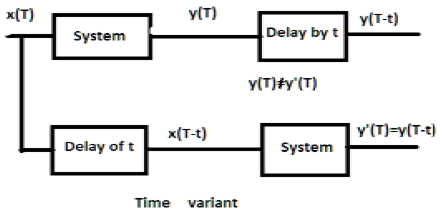
a) $y(T) = x(2T)$
यदि उपरोक्त अभिव्यक्ति, यह पहले सिस्टम के माध्यम से और फिर समय की देरी से गुजरता है (जैसा कि आंकड़े के ऊपरी हिस्से में दिखाया गया है); तब आउटपुट बन जाएगा$x(2T-2t)$। अब, उसी अभिव्यक्ति को पहले एक समय की देरी से और फिर सिस्टम के माध्यम से पारित किया जाता है (जैसा कि आंकड़े के निचले हिस्से में दिखाया गया है)। आउटपुट बन जाएगा$x(2T-t)$।
इसलिए, प्रणाली एक समय-अपरिवर्तनीय प्रणाली नहीं है।
b) $y(T) = \sin [x(T)]$
यदि सिग्नल पहले सिस्टम के माध्यम से और फिर समय की देरी प्रक्रिया के माध्यम से पारित किया जाता है, तो आउटपुट हो सकता है $\sin x(T-t)$। इसी प्रकार, यदि सिस्टम को पहले देरी के माध्यम से पारित किया जाता है तो सिस्टम के माध्यम से फिर आउटपुट होगा$\sin x(T-t)$। हम स्पष्ट रूप से देख सकते हैं कि दोनों आउटपुट समान हैं। इसलिए, सिस्टम समय अपरिवर्तनीय है।
एक समय संस्करण प्रणाली के लिए, आउटपुट और इनपुट में कुछ समय के लिए देरी हो सकती है, लेकिन इनपुट में देरी आउटपुट पर प्रतिबिंबित नहीं होनी चाहिए। सभी समय स्केलिंग के मामले समय संस्करण प्रणाली के उदाहरण हैं। इसी तरह, जब सिस्टम रिलेशनशिप में गुणांक समय का एक फ़ंक्शन होता है, तब भी, सिस्टम टाइम वेरिएंट होता है।
उदाहरण
a) $y(t) = x[\cos T]$
यदि उपरोक्त संकेत पहले सिस्टम के माध्यम से और फिर समय की देरी के माध्यम से पारित किया जाता है, तो आउटपुट होगा $x\cos (T-t)$। यदि इसे पहले देरी से और फिर सिस्टम के माध्यम से पारित किया जाता है, तो यह होगा$x(\cos T-t)$। चूंकि आउटपुट एक जैसे नहीं होते हैं, सिस्टम टाइम वेरिएंट होता है।
b) $y(T) = \cos T.x(T)$
यदि उपरोक्त अभिव्यक्ति को पहले सिस्टम के माध्यम से और फिर समय की देरी के माध्यम से पारित किया जाता है, तो आउटपुट होगा $\cos(T-t)x(T-t)$। हालांकि, यदि अभिव्यक्ति को पहले समय और फिर सिस्टम के माध्यम से पारित किया जाता है, तो आउटपुट होगा$\cos T.x(T-t)$। जैसा कि आउटपुट समान नहीं हैं, स्पष्ट रूप से सिस्टम समय रूप है।
एक स्थिर प्रणाली BIBO (बाध्य आउटपुट के लिए बाध्य इनपुट) को संतुष्ट करती है। यहाँ, बंधे का मतलब आयाम में परिमित है। एक स्थिर प्रणाली के लिए, आउटपुट को परिमित या सीमित इनपुट के लिए परिमित या सीमित किया जाना चाहिए, हर समय।
बंधे हुए इनपुट के कुछ उदाहरण साइन, कोसाइन, डीसी, साइनम और यूनिट स्टेप के कार्य हैं।
उदाहरण
a) $y(t) = x(t)+10$
यहां, एक निश्चित बाउंड इनपुट के लिए, हम निश्चित बाउंडेड आउटपुट प्राप्त कर सकते हैं अर्थात यदि हम डालते हैं $x(t) = 2, y(t) = 12$जो प्रकृति में बँधा हुआ है। इसलिए, सिस्टम स्थिर है।
b) $y(t) = \sin [x(t)]$
दी गई अभिव्यक्ति में, हम जानते हैं कि साइन फ़ंक्शंस में मूल्यों की एक निश्चित सीमा होती है, जो -1 से +1 के बीच होती है। इसलिए, हम x (t) में जो भी मान रखेंगे, हम अपनी सीमा के भीतर मान प्राप्त करेंगे। इसलिए, सिस्टम स्थिर है।
अस्थिर सिस्टम BIBO स्थितियों को संतुष्ट नहीं करते हैं। इसलिए, एक बंधे हुए इनपुट के लिए, हम अस्थिर प्रणालियों के मामले में एक बंधे हुए आउटपुट की उम्मीद नहीं कर सकते।
उदाहरण
a) $y(t) = tx(t)$
यहाँ, एक परिमित इनपुट के लिए, हम एक परिमित आउटपुट की अपेक्षा नहीं कर सकते हैं। उदाहरण के लिए, अगर हम डाल देंगे$x(t) = 2 \Rightarrow y(t) = 2t$। यह एक परिमित मूल्य नहीं है क्योंकि हम टी के मूल्य को नहीं जानते हैं। इसलिए, इसे कहीं से भी लगाया जा सकता है। इसलिए, यह प्रणाली स्थिर नहीं है। यह एक अस्थिर प्रणाली है।
b) $y(t) = \frac{x(t)}{\sin t}$
हमने पहले चर्चा की है, कि साइन फ़ंक्शन में -1 से +1 तक एक निश्चित सीमा होती है; लेकिन यहाँ, यह हर में मौजूद है। तो, सबसे खराब स्थिति में, यदि हम t = 0 डालते हैं और साइन फंक्शन शून्य हो जाता है, तो पूरी प्रणाली अनंत हो जाएगी। इसलिए, इस प्रकार की प्रणाली बिल्कुल स्थिर नहीं है। जाहिर है, यह एक अस्थिर प्रणाली है।
Example 1 - जाँच करें कि क्या $y(t) = x*(t)$ रैखिक या गैर-रैखिक है।
Solution- फ़ंक्शन इनपुट के संयुग्म का प्रतिनिधित्व करता है। यह या तो एकरूपता के पहले कानून और नशे की लत के कानून या दो नियमों द्वारा सत्यापित किया जा सकता है। हालांकि, नियमों के माध्यम से पुष्टि करना बहुत आसान है, इसलिए हम इसके द्वारा जाएंगे।
यदि सिस्टम में इनपुट शून्य है, तो आउटपुट भी शून्य हो जाता है। इसलिए, हमारी पहली शर्त संतुष्ट है। इनपुट पर न तो कोई नॉन-लीनियर ऑपरेटर इस्तेमाल होता है और न ही आउटपुट। इसलिए, सिस्टम रैखिक है।
Example 2 - जाँच करें कि क्या $y(t)=\begin{cases}x(t+1), & t > 0\\x(t-1), & t\leq 0\end{cases}$ रैखिक या गैर रेखीय है
Solution- स्पष्ट रूप से, हम देख सकते हैं कि जब शून्य शून्य से कम या बराबर हो जाता है तो इनपुट शून्य हो जाता है। तो, हम कह सकते हैं कि शून्य इनपुट पर आउटपुट भी शून्य है और हमारी पहली शर्त संतुष्ट है।
फिर से, न तो इनपुट पर और न ही आउटपुट पर गैर-रेखीय ऑपरेटर का उपयोग किया जाता है। इसलिए, सिस्टम रैखिक है।
Example 3 - जाँच करें कि क्या $y(t) = \sin t.x(t)$ स्थिर है या नहीं।
Solution - मान लीजिए, हमने x (t) के मान को 3 के रूप में लिया है। यहां, साइन फ़ंक्शन को इसके साथ गुणा किया गया है और साइन फ़ंक्शन का अधिकतम और न्यूनतम मान -1 से +1 के बीच भिन्न होता है।
इसलिए, पूरे फ़ंक्शन का अधिकतम और न्यूनतम मूल्य भी -3 और +3 के बीच भिन्न होगा। इस प्रकार, सिस्टम स्थिर है क्योंकि यहां हमें एक बंधे हुए आउटपुट के लिए एक बाध्य इनपुट मिल रहा है।
ऊर्जा और बिजली संकेतों के लिए असतत समय फूरियर ट्रांसफॉर्म (DTFT) मौजूद है। ज़ेड-ट्रांसफ़ॉर्मेशन न तो ऊर्जा और न ही पावर (एनईएनपी) टाइप सिग्नल के लिए मौजूद है, केवल एक निश्चित सीमा तक। प्रतिस्थापन$z=e^{jw}$ का उपयोग Z- रूपांतरण के लिए DTFT रूपांतरण के लिए किया जाता है, केवल बिल्कुल संकेत के लिए।
तो, एक बिजली श्रृंखला में असतत समय सिग्नल x (n) के Z- रूपांतर को लिखा जा सकता है -
$$X(z) = \sum_{n-\infty}^\infty x(n)Z^{-n}$$उपरोक्त समीकरण दो-पक्षीय जेड-ट्रांसफ़ॉर्म समीकरण का प्रतिनिधित्व करता है।
आमतौर पर, जब कोई सिग्नल Z- रूपांतरित होता है, तो इसे निम्न रूप में दर्शाया जा सकता है -
$$X(Z) = Z[x(n)]$$या $x(n) \longleftrightarrow X(Z)$
यदि यह एक निरंतर समय संकेत है, तो जेड-ट्रांसफॉर्म की आवश्यकता नहीं है क्योंकि लाप्लास ट्रांसफॉर्मेशन का उपयोग किया जाता है। हालांकि, असतत समय संकेतों का विश्लेषण केवल जेड-ट्रांसफॉर्म के माध्यम से किया जा सकता है।
अभिसरण का क्षेत्र
कन्वर्जेंस का क्षेत्र जेड-प्लेन में जटिल वैरिएबल Z की श्रेणी है। संकेत का Z- परिवर्तन परिमित या अभिसरण है। तो, ROC Z के मानों के उन सेटों का प्रतिनिधित्व करता है, जिनके लिए X (Z) का परिमित मूल्य है।
आरओसी के गुण
- आरओसी में कोई पोल शामिल नहीं है।
- दाएं तरफा संकेत के लिए, आरओसी जेड-प्लेन में सर्कल के बाहर होगा।
- बाएं तरफा सिग्नल के लिए, आरओसी जेड-प्लेन में सर्कल के अंदर होगा।
- स्थिरता के लिए, आरओसी में जेड-प्लेन में यूनिट सर्कल शामिल है।
- दोनों पक्षीय संकेत के लिए, आरओसी जेड-प्लेन में एक रिंग है।
- परिमित अवधि के संकेत के लिए, आरओसी संपूर्ण जेड-प्लेन है।
Z- रूपांतर इसकी विशिष्ट विशेषता है -
- एक्स (जेड) की अभिव्यक्ति
- X (Z) का ROC
सिग्नल और उनके आरओसी
| एक्स (एन) | एक्स (जेड) | रूह |
|---|---|---|
| $\delta(n)$ | $1$ | पूरा जेड प्लेन |
| $U(n)$ | $1/(1-Z^{-1})$ | मॉड (जेड)> 1 |
| $a^nu(n)$ | $1/(1-aZ^{-1})$ | मॉड (जेड)> मॉड (क) |
| $-a^nu(-n-1)$ | $1/(1-aZ^{-1})$ | मॉड (जेड) <मॉड (क) |
| $na^nu(n)$ | $aZ^{-1}/(1-aZ^{-1})^2$ | मॉड (जेड)> मॉड (क) |
| $-a^nu(-n-1)$ | $aZ^{-1}/(1-aZ^{-1})^2$ | मॉड (जेड) <मॉड (क) |
| $U(n)\cos \omega n$ | $(Z^2-Z\cos \omega)/(Z^2-2Z \cos \omega +1)$ | मॉड (जेड)> 1 |
| $U(n)\sin \omega n$ | $(Z\sin \omega)/(Z^2-2Z \cos \omega +1)$ | मॉड (जेड)> 1 |
उदाहरण
हमें दिए गए सिग्नल के Z- ट्रांसफ़ॉर्मेशन और ROC को ढूंढना चाहिए $x(n) = \lbrace 7,3,4,9,5\rbrace$, जहां श्रृंखला का मूल 3 पर है।
Solution - हमारे पास जो फॉर्मूला है उसे लागू करना -
$X(z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-1}^3 x(n)Z^{-n}$
$= x(-1)Z+x(0)+x(1)Z^{-1}+x(2)Z^{-2}+x(3)Z^{-3}$
$= 7Z+3+4Z^{-1}+9Z^{-2}+5Z^{-3}$
ROC, Z = 0, ∞,-Z को छोड़कर संपूर्ण Z- विमान है
इस अध्याय में, हम Z- परिवर्तनों के मूल गुणों को समझेंगे।
रैखिकता
यह बताता है कि जब दो या अधिक व्यक्तिगत असतत संकेतों को स्थिरांक से गुणा किया जाता है, तो उनके संबंधित Z- परिवर्तन भी उसी स्थिरांक से गुणा किए जाएंगे।
गणित के अनुसार,
$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$Proof - हम जानते हैं कि,
$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$
$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= a_1X_1(z)+a_2X_2(z)$ (इसलिए साबित)
यहां, आरओसी है $ROC_1\bigcap ROC_2$।
समय बदलता है
प्रॉपर्टी शिफ्टिंग में यह दर्शाया गया है कि असतत सिग्नल में टाइम डोमेन में परिवर्तन जेड-डोमेन को कैसे प्रभावित करेगा, जिसे इस प्रकार लिखा जा सकता है;
$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$या $x(n-1)\longleftrightarrow Z^{-1}X(Z)$
Proof -
लश्कर $y(P) = X(P-K)$
$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$
$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$
आज्ञा देना = पीके
$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$
$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$
$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$
$= Z^{-k}X(Z)$ (इसलिए साबित)
यहाँ, ROC को Z = 0 (p> 0) या Z = p (p <0) के रूप में लिखा जा सकता है
उदाहरण
U (n) और U (n-1) को निम्नानुसार प्लॉट किया जा सकता है
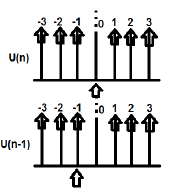
U (n) कैब के Z- परिवर्तन के रूप में लिखा जा सकता है;
$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$
U (Z-1) के Z- परिवर्तन के रूप में लिखा जा सकता है;
$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$
अच्छा यहाँ $x(n-n_0) = Z^{-n_0}X(Z)$ (इसलिए साबित)
टाइम स्केलिंग
टाइम स्केलिंग प्रॉपर्टी हमें बताती है, जब समय के असतत रूप में स्केल किया जाता है, तो सिग्नल का Z- डोमेन क्या होगा, जिसे लिखा जा सकता है;
$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$Proof -
लश्कर $y(p) = a^{p}x(p)$
$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$
$= X(a^{-1}Z)$(इसलिए)
ROC: = mod (ar1) <mod (Z) <mod (ar2) जहां mod = modulus है
उदाहरण
आइए हम Z- परिवर्तन का निर्धारण करते हैं $x(n) = a^n \cos \omega n$ समय स्केलिंग संपत्ति का उपयोग करना।
Solution -
हम पहले से ही जानते हैं कि संकेत का जेड-परिवर्तन $\cos (\omega n)$ द्वारा दिया गया है -
$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$
अब, टाइम स्केलिंग संपत्ति को लागू करना, का Z- परिवर्तन $a^n \cos \omega n$ के रूप में लिखा जा सकता है;
$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$
$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$
$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$
क्रमिक विभेदीकरण
क्रमिक विभेदीकरण गुण से पता चलता है कि जब हम समय क्षेत्र में समय के संबंध में असतत संकेत को अलग करते हैं तो Z- परिवर्तन होगा। यह नीचे दिखाया गया है।
$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$Proof -
समीकरण के LHS पर विचार करें - $\frac{dx(n)}{dn}$
$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$$= x(n)-X(n-1)$
$= x(Z)-Z^{-1}x(Z)$
$= (1-Z^{-1})x(Z)$ (इसलिए साबित)
ROC: R1 <Mod (Z) <R2
उदाहरण
आइए हम दिए गए संकेत के Z- परिवर्तन को खोजें $x(n) = n^2u(n)$
संपत्ति से हम लिख सकते हैं
$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$
$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$
$= Z/((Z-1)^2$
$= y(let)$
अब, Z [ny] को संपत्ति को फिर से लागू करके पता लगाया जा सकता है,
$Z(n,y) = -Z\frac{dy}{dz}$
$= -Z\frac{d[Z/(Z-1)^3]}{dz}$
$= Z(Z+1)/(Z-1)^2$
कनवल्शन
यह सिस्टम के Z- डोमेन में बदलाव को दर्शाता है जब एक असततता असतत सिग्नल फॉर्म में होती है, जिसे इस प्रकार लिखा जा सकता है -
$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$
Proof -
$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$
चलो nk = l, तो उपरोक्त समीकरण टैक्सी के रूप में लिखा जाना चाहिए -
$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$
$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$
$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$
$= X_1(Z).X_2(Z)$ (इसलिए साबित)
आरओसी:$ROC\bigcap ROC2$
उदाहरण
आइए हम दो संकेतों द्वारा दिए गए दृढ़ संकल्प को खोजें
$x_1(n) = \lbrace 3,-2,2\rbrace$ ... (eq 1)
$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ... (eq 2)
पहले समीकरण के Z- परिवर्तन के रूप में लिखा जा सकता है;
$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$
$= 3-2Z^{-1}+2Z^{-2}$
दूसरे संकेत के Z- परिवर्तन के रूप में लिखा जा सकता है;
$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
तो, ऊपर दिए गए दो संकेतों का दृढ़ संकल्प है -
$X(Z) = [x_1(Z)^*x_2(Z)]$
$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$
उलटा Z- परिवर्तन हम ले,
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$
प्रारंभिक मूल्य प्रमेय
यदि x (n) एक कारण अनुक्रम है, जिसमें X (z) के रूप में इसका Z- परिवर्तन है, तो प्रारंभिक मूल्य प्रमेय के रूप में लिखा जा सकता है;
$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$
Proof - हम जानते हैं कि,
$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$
उपरोक्त श्रृंखला का विस्तार करते हुए, हम प्राप्त करते हैं;
$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
उपरोक्त मामले में यदि Z →। तब $Z^{-n}\rightarrow 0$ (क्योंकि n> 0)
इसलिए, हम कह सकते हैं;
$\lim_{z \to \infty}X(z) = X(0)$ (इसलिए साबित)
अंतिम मूल्य प्रमेय
फाइनल वैल्यू प्रमेय में कहा गया है कि यदि किसी सिग्नल के Z- ट्रांसफॉर्मेशन को X (Z) के रूप में दर्शाया जाता है और डंडे सभी सर्कल के अंदर होते हैं, तो उसके फाइनल वैल्यू को x (n) या X (∞) के रूप में दर्शाया जाता है और इसे लिखा जा सकता है। -
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$
Conditions -
- यह केवल कारण प्रणालियों के लिए लागू है।
- $X(Z)(1-Z^{-1})$ जेड-प्लेन में यूनिट सर्कल के अंदर पोल होना चाहिए।
Proof - हम जानते हैं कि
$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$
$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$
$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$
यहां, हम एक तरफा जेड-परिवर्तन की उन्नत संपत्ति को लागू कर सकते हैं। तो, उपरोक्त समीकरण को फिर से लिखा जा सकता है;
$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$
अब उपरोक्त समीकरण में z = 1 डालते हैं, हम उपरोक्त समीकरण का विस्तार कर सकते हैं -
$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$
इस रूप में तैयार किया जा सकता है;
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(इसलिए साबित)
उदाहरण
आइए x (n) का आरंभिक और अंतिम मान ज्ञात करें जिसका संकेत किसके द्वारा दिया गया है
$X(Z) = 2+3Z^{-1}+4Z^{-2}$
Solution - हमें पहले, प्रमेय को लागू करके संकेत के प्रारंभिक मूल्य का पता लगाएं
$x(0) = \lim_{z \to \infty}X(Z)$
$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$
$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$
अब हमें प्रमेय को लागू करने वाले सिग्नल का अंतिम मान ज्ञात करते हैं
$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$
$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$
$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$
$= 2+1+1-4 = 0$
Some other properties of Z-transform are listed below -
फ्रीक्वेंसी में अंतर
यह सिग्नल के जेड-डोमेन में परिवर्तन देता है, जब इसके असतत सिग्नल को समय के संबंध में विभेदित किया जाता है।
$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$
इसकी आरओसी के रूप में लिखा जा सकता है;
$r_2< Mod(Z)< r_1$
उदाहरण
आइए आवृत्ति में विभेदन के माध्यम से x (n) का मान ज्ञात करें, जिसका Z- डोमेन में असतत संकेत द्वारा दिया गया है $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$
संपत्ति से, हम लिख सकते हैं कि
$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$
$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$
$= (aZ^{-1})/(1+aZ^{-1})$
$= 1-1/(1+aZ^{-1})$
$nx(n) = \delta(n)-(-a)^nu(n)$
$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$
समय में गुणा
यह सिग्नल के जेड-डोमेन में बदलाव देता है जब असतत सिग्नल स्तर पर गुणा होता है।
$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$
समय में समझौता
यह Z- डोमेन में संयुग्मित असतत संकेत के प्रतिनिधित्व को दर्शाता है।
$X^*(n)\longleftrightarrow X^*(Z^*)$
एक प्रणाली, जिसमें सिस्टम फ़ंक्शन होता है, केवल तभी स्थिर हो सकता है जब सभी पोल यूनिट सर्कल के अंदर झूठ बोलते हैं। सबसे पहले, हम जांचते हैं कि सिस्टम कार्य-कारण है या नहीं। यदि सिस्टम कोसल है, तो हम इसके बीआईबीओ स्थिरता निर्धारण के लिए जाते हैं; जहां BIBO स्थिरता बाउंड आउटपुट स्थिति के लिए बंधे इनपुट को संदर्भित करता है।
इसे इस प्रकार लिखा जा सकता है;
$Mod(X(Z))< \infty$
$= Mod(\sum x(n)Z^{-n})< \infty$
$= \sum Mod(x(n)Z^{-n})< \infty$
$= \sum Mod[x(n)(re^{jw})^{-n}]< 0$
$= \sum Mod[x(n)r^{-n}]Mod[e^{-jwn}]< \infty$
$= \sum_{n = -\infty}^\infty Mod[x(n)r^{-n}]< \infty$
उपरोक्त समीकरण जेड-परिवर्तन के अस्तित्व के लिए स्थिति को दर्शाता है।
हालाँकि, DTFT सिग्नल के अस्तित्व की शर्त है
$$\sum_{n = -\infty}^\infty Mod(x(n)< \infty$$उदाहरण 1
आइए हम सिग्नल के जेड-ट्रांसफॉर्मेशन का पता लगाने की कोशिश करें, जो कि नीचे दिया गया है
$x(n) = -(-0.5)^{-n}u(-n)+3^nu(n)$
$= -(-2)^nu(n)+3^nu(n)$
Solution - यहाँ, के लिए $-(-2)^nu(n)$ ROC लेफ्ट साइडेड है और Z <2 है
के लिये $3^nu(n)$ ROC सही पक्षीय है और Z> 3
इसलिए, यहाँ संकेत का Z- रूपांतर मौजूद नहीं होगा क्योंकि कोई सामान्य क्षेत्र नहीं है।
उदाहरण 2
आइए हम दिए गए सिग्नल के जेड-ट्रांसफॉर्म का पता लगाने की कोशिश करते हैं
$x(n) = -2^nu(-n-1)+(0.5)^nu(n)$
Solution - यहाँ, के लिए $-2^nu(-n-1)$ सिग्नल का आरओसी लेफ्ट साइडेड है और Z <2 है
संकेत के लिए $(0.5)^nu(n)$ आरओसी सही पक्षीय है और जेड> 0.5 है
तो, आम आरओसी का गठन 0.5 <Z <2 के रूप में किया जा रहा है
इसलिए, Z- परिवर्तन के रूप में लिखा जा सकता है;
$X(Z) = \lbrace\frac{1}{1-2Z^{-1}}\rbrace+\lbrace\frac{1}{(1-0.5Z)^{-1}}\rbrace$
उदाहरण 3
आइए हम सिग्नल के जेड-ट्रांसफॉर्मेशन का पता लगाने की कोशिश करें, जो कि नीचे दिया गया है $x(n) = 2^{r(n)}$
Solution- r (n) रैंप सिग्नल है। तो संकेत के रूप में लिखा जा सकता है;
$x(n) = 2^{nu(n)}\lbrace 1, n<0 (u(n)=0)\quad and\quad2^n, n\geq 0(u(n) = 1)\rbrace$
$= u(-n-1)+2^nu(n)$
यहाँ, संकेत के लिए $u(-n-1)$ और आरओसी जेड <1 और के लिए $2^nu(n)$ ROC के साथ Z> 2 है।
तो, संकेत का Z- परिवर्तन मौजूद नहीं होगा।
जेड-क्रॉसल सिस्टम के लिए ट्रांसफॉर्मर
कारण के रूप में परिभाषित किया जा सकता है $h(n) = 0,n<0$। कारण प्रणाली के लिए, आरओसी जेड-प्लेन में सर्कल के बाहर होगा।
$H(Z) = \displaystyle\sum\limits_{n = 0}^{\infty}h(n)Z^{-n}$
उपरोक्त समीकरण का विस्तार,
$H(Z) = h(0)+h(1)Z^{-1}+h(2)Z^{-2}+...\quad...\quad...$
$= N(Z)/D(Z)$
कारण प्रणालियों के लिए, ट्रांसफर फ़ंक्शन के विस्तार में जेड की सकारात्मक शक्तियां शामिल नहीं हैं। कारण प्रणाली के लिए, अंश का क्रम संप्रेषक के आदेश से अधिक नहीं हो सकता। इसे इस प्रकार लिखा जा सकता है-
$\lim_{z \rightarrow \infty}H(Z) = h(0) = 0\quad or\quad Finite$
कारण प्रणाली की स्थिरता के लिए, ट्रांसफर फ़ंक्शन के डंडे जेड-प्लेन में यूनिट सर्कल के अंदर होना चाहिए।
एंटी-कारण प्रणाली के लिए Z- परिवर्तन
विरोधी कारण प्रणाली के रूप में परिभाषित किया जा सकता है $h(n) = 0, n\geq 0$। एंटी-कारण प्रणाली के लिए, ट्रांसफर फ़ंक्शन के डंडे जेड-प्लेन में यूनिट सर्कल के बाहर झूठ होना चाहिए। विरोधी-कारण प्रणाली के लिए, आरओसी जेड-प्लेन में सर्कल के अंदर होगा।
यदि हम एक सिस्टम का विश्लेषण करना चाहते हैं, जो पहले से ही आवृत्ति डोमेन में दर्शाया गया है, असतत समय संकेत के रूप में तो हम व्युत्क्रम जेड-परिवर्तन के लिए जाते हैं।
गणितीय रूप से, इसे इस रूप में दर्शाया जा सकता है;
$$x(n) = Z^{-1}X(Z)$$जहाँ x (n) समय क्षेत्र में संकेत है और X (Z) आवृत्ति डोमेन में संकेत है।
यदि हम अभिन्न प्रारूप में उपरोक्त समीकरण का प्रतिनिधित्व करना चाहते हैं तो हम इसे लिख सकते हैं
$$x(n) = (\frac{1}{2\Pi j})\oint X(Z)Z^{-1}dz$$यहां, इंटीग्रल एक बंद पथ सी पर है। यह पथ एक्स (जेड) के आरओसी के भीतर है और इसमें मूल शामिल है।
व्युत्क्रम जेड-ट्रांसफ़ॉर्म खोजने की विधियाँ
जब असतत प्रारूप में विश्लेषण की आवश्यकता होती है, तो हम उलटा Z- परिवर्तन के माध्यम से आवृत्ति डोमेन सिग्नल को असतत प्रारूप में परिवर्तित करते हैं। उलटा Z- परिवर्तन निर्धारित करने के लिए हम निम्नलिखित चार तरीके अपनाते हैं।
- लंबी विभाजन प्रणाली
- आंशिक विवर्तन विस्तार विधि
- अवशेष या कंटूर अभिन्न विधि
लंबी विभाजन प्रणाली
इस विधि में, संकेत x (z) के Z- परिवर्तन को नीचे दिखाए गए अनुसार बहुपद के अनुपात के रूप में दर्शाया जा सकता है;
$$x(z)=N(Z)/D(Z)$$अब, यदि हम भाजक को भाजक से विभाजित करते हैं, तो हमें नीचे दिखाए गए अनुसार एक श्रृंखला मिलेगी
$$X(z) = x(0)+x(1)Z^{-1}+x(2)Z^{-2}+...\quad...\quad...$$उपरोक्त अनुक्रम दिए गए संकेत के व्युत्क्रम Z- परिवर्तन की श्रृंखला का प्रतिनिधित्व करता है (n series0 के लिए) और उपरोक्त प्रणाली कारण है।
हालाँकि n <0 के लिए श्रृंखला के रूप में लिखा जा सकता है;
$$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...\quad...\quad...$$आंशिक अंश विस्तार विधि
यहाँ भी संकेत पहले N (z) / D (z) फॉर्म में व्यक्त किया गया है।
यदि यह एक तर्कसंगत अंश है तो इसे निम्नानुसार दर्शाया जाएगा;
$x(z) = b_0+b_1Z^{-1}+b_2Z^{-2}+...\quad...\quad...+b_mZ^{-m})/(a_0+a_1Z^{-1}+a_2Z^{-2}+...\quad...\quad...+a_nZ^{-N})$
M <n और। 0 होने पर उपरोक्त एक अनुचित है
यदि अनुपात उचित नहीं है (यानी अनुचित), तो हमें इसे हल करने के लिए उचित रूप में बदलना होगा।
अवशेष या कंटूर इंटीग्रल विधि
इस पद्धति में, हम संक्षेप के अवशेषों द्वारा व्युत्क्रम Z- परिवर्तन x (n) प्राप्त करते हैं $[x(z)Z^{n-1}]$सभी डंडों पर। गणितीय रूप से, इसे इस रूप में व्यक्त किया जा सकता है
$$x(n) = \displaystyle\sum\limits_{all\quad poles\quad X(z)}residues\quad of[x(z)Z^{n-1}]$$यहाँ, आदेश m के किसी भी पोल के लिए अवशेष $z = \beta$ है
$$Residues = \frac{1}{(m-1)!}\lim_{Z \rightarrow \beta}\lbrace \frac{d^{m-1}}{dZ^{m-1}}\lbrace (z-\beta)^mX(z)Z^{n-1}\rbrace$$उदाहरण 1
सिस्टम की प्रतिक्रिया का पता लगाएं $s(n+2)-3s(n+1)+2s(n) = \delta (n)$, जब सभी प्रारंभिक शर्तें शून्य हैं।
Solution - उपरोक्त समीकरण के दोनों किनारों पर Z- रूपांतर करने पर, हमें मिलता है
$$S(z)Z^2-3S(z)Z^1+2S(z) = 1$$$\Rightarrow S(z)\lbrace Z^2-3Z+2\rbrace = 1$
$\Rightarrow S(z) = \frac{1}{\lbrace z^2-3z+2\rbrace}=\frac{1}{(z-2)(z-1)} = \frac{\alpha _1}{z-2}+\frac{\alpha _2}{z-1}$
$\Rightarrow S(z) = \frac{1}{z-2}-\frac{1}{z-1}$
उपरोक्त समीकरण के व्युत्क्रम जेड-परिवर्तन को लेते हुए, हम प्राप्त करते हैं
$S(n) = Z^{-1}[\frac{1}{Z-2}]-Z^{-1}[\frac{1}{Z-1}]$
$= 2^{n-1}-1^{n-1} = -1+2^{n-1}$
उदाहरण 2
सिस्टम फंक्शन H (z) और यूनिट सैंपल रिस्पॉन्स h (n) सिस्टम का पता लगाएं जिसका अंतर समीकरण नीचे वर्णित है
$y(n) = \frac{1}{2}y(n-1)+2x(n)$
जहाँ, y (n) और x (n) क्रमशः सिस्टम का आउटपुट और इनपुट हैं।
Solution - उपरोक्त अंतर समीकरण के Z- परिवर्तन को लेते हुए, हम प्राप्त करते हैं
$y(z) = \frac{1}{2}Z^{-1}Y(Z)+2X(z)$
$= Y(Z)[1-\frac{1}{2}Z^{-1}] = 2X(Z)$
$= H(Z) = \frac{Y(Z)}{X(Z)} = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$
इस प्रणाली में एक पोल है $Z = \frac{1}{2}$ तथा $Z = 0$ तथा $H(Z) = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$
इसलिए, ऊपर के उलटा Z- रूपांतर लेते हुए, हम प्राप्त करते हैं
$h(n) = 2(\frac{1}{2})^nU(n)$
उदाहरण 3
निम्नलिखित मामले में Y (z), n≥0 निर्धारित करें -
$y(n)+\frac{1}{2}y(n-1)-\frac{1}{4}y(n-2) = 0\quad given\quad y(-1) = y(-2) = 1$
Solution - उपरोक्त समीकरण के लिए Z- परिवर्तन लागू करना, हम प्राप्त करते हैं
$Y(Z)+\frac{1}{2}[Z^{-1}Y(Z)+Y(-1)]-\frac{1}{4}[Z^{-2}Y(Z)+Z^{-1}Y(-1)+4(-2)] = 0$
$\Rightarrow Y(Z)+\frac{1}{2Z}Y(Z)+\frac{1}{2}-\frac{1}{4Z^2}Y(Z)-\frac{1}{4Z}-\frac{1}{4} = 0$
$\Rightarrow Y(Z)[1+\frac{1}{2Z}-\frac{1}{4Z^2}] =\frac{1}{4Z}-\frac{1}{2}$
$\Rightarrow Y(Z)[\frac{4Z^2+2Z-1}{4Z^2}] = \frac{1-2Z}{4Z}$
$\Rightarrow Y(Z) = \frac{Z(1-2Z)}{4Z^2+2Z-1}$
निरंतर समय सिग्नल फूरियर रूपांतरण की तरह, असतत समय फूरियर ट्रांसफॉर्म का उपयोग इसके बराबर आवृत्ति डोमेन प्रतिनिधित्व और LTI असतत समय प्रणाली में एक असतत अनुक्रम का प्रतिनिधित्व करने के लिए किया जा सकता है और विभिन्न कम्प्यूटेशनल एल्गोरिदम विकसित कर सकते हैं।
एक्स (j function) निरंतर एफटी में, एक्स (एन) का एक निरंतर कार्य है। हालाँकि, DFT अपने स्पेक्ट्रम X (।) के नमूनों के साथ x (n) का प्रतिनिधित्व करने से संबंधित है। इसलिए, यह गणितीय उपकरण सुविधाजनक प्रतिनिधित्व में कम्प्यूटेशनल रूप से बहुत महत्व रखता है। दोनों, आवधिक और गैर-आवधिक अनुक्रमों को इस उपकरण के माध्यम से संसाधित किया जा सकता है। आवधिक अनुक्रमों को अवधि को अनंत तक विस्तारित करके नमूना बनाने की आवश्यकता है।
फ़्रीक्वेंसी डोमेन सैंपलिंग
परिचय से, यह स्पष्ट है कि हमें यह जानने की जरूरत है कि आवृत्ति डोमेन नमूनाकरण (सैंपलिंग एक्स) (ω) के माध्यम से कैसे आगे बढ़ना है। इसलिए, नमूना फूरियर रूपांतरण और डीएफटी के बीच संबंध निम्नलिखित तरीके से स्थापित किया गया है।
इसी प्रकार, आवधिक क्रम एन से अनंत तक की अवधि का विस्तार करके इस उपकरण के लिए फिट हो सकते हैं।
एक गैर आवधिक अनुक्रम हो, $X(n) = \lim_{N \to \infty}x_N(n)$
अपने फूरियर रूपांतरण को परिभाषित करते हुए,
$X(\omega ) = \sum_{n=-\infty}^\infty x(n)e^{-jwn}X(K\delta \omega)$
यहां, हर (रेडियन अंतराल पर X (ω) का समय-समय पर नमूना लिया जाता है।
जैसा कि X (ians) 2 (रेडियन में आवधिक है, हमें केवल मौलिक रेंज में नमूनों की आवश्यकता होती है। नमूनों को आवृत्ति रेंज 0π2 equ में समकालिक अंतराल के बाद लिया जाता है। बराबर अंतराल के बीच अंतर है$\delta \omega = \frac{2\pi }{N}k$ रेडियन।
अब मूल्यांकन कर रहा है, $\omega = \frac{2\pi}{N}k$
$X(\frac{2\pi}{N}k) = \sum_{n = -\infty}^\infty x(n)e^{-j2\pi nk/N},$ ... eq (2)
जहां k = 0,1, …… N-1
ऊपर उपविभाजित करने के बाद, और सम्मिश्रण के क्रम को बदलना
$X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}[\displaystyle\sum\limits_{l = -\infty}^\infty x(n-Nl)]e^{-j2\pi nk/N}$ ... eq (3)
$\sum_{l=-\infty}^\infty x(n-Nl) = x_p(n) = a\quad periodic\quad function\quad of\quad period\quad N\quad and\quad its\quad fourier\quad series\quad = \sum_{k = 0}^{N-1}C_ke^{j2\pi nk/N}$
जहाँ, n = 0,1,… .., एन -1; 'पी'- का मतलब आवधिक इकाई या कार्य है
फूरियर गुणांक हैं,
$C_k = \frac{1}{N}\sum_{n = 0}^{N-1}x_p(n)e^{-j2\pi nk/N}$k = 0,1,…, N-1 ... eq (4)
3 और 4 के समीकरणों की तुलना करें, तो हम प्राप्त करते हैं;
$NC_k = X(\frac{2\pi}{N}k)$k = 0,1,…, N-1 ... eq (5)
$NC_k = X(\frac{2\pi}{N}k) = X(e^{jw}) = \displaystyle\sum\limits_{n = -\infty}^\infty x_p(n)e^{-j2\pi nk/N}$... eq (6)
फूरियर श्रृंखला विस्तार से,
$x_p(n) = \frac{1}{N}\displaystyle\sum\limits_{k = 0}^{N-1}NC_ke^{j2\pi nk/N} = \frac{1}{N}\sum_{k = 0}^{N-1}X(\frac{2\pi}{N}k)e^{j2\pi nk/N}$... eq (7)
जहां n = 0,1,…, एन -1
यहां, हमें एक्स (।) से आवधिक संकेत मिला। $x(n)$ से निकाला जा सकता है $x_p(n)$ केवल, यदि समय डोमेन में कोई उपद्रव नहीं है। $N\geq L$
एन = की अवधि $x_p(n)$ एल = की अवधि $x(n)$
$x(n) = \begin{cases}x_p(n), & 0\leq n\leq N-1\\0, & Otherwise\end{cases}$
इस तरीके से मैपिंग हासिल की जाती है।
डीएफटी के गुण
रैखिकता
यह बताता है कि संकेतों के संयोजन का डीएफटी व्यक्तिगत संकेतों के डीएफटी के योग के बराबर है। आइए हम दो संकेत लेते हैं x 1 (n) और x 2 (n), जिनके DFT s क्रमशः X 1 (ω) और X 2 ( X ) हैं। तो अगर
$x_1(n)\rightarrow X_1(\omega)$तथा$x_2(n)\rightarrow X_2(\omega)$
फिर $ax_1(n)+bx_2(n)\rightarrow aX_1(\omega)+bX_2(\omega)$
कहाँ पे a तथा b निरंतर हैं।
समरूपता
डीएफटी के समरूपता गुणों को उसी तरह से प्राप्त किया जा सकता है जैसे हमने डीटीएफटी समरूपता गुणों को प्राप्त किया है। हम जानते हैं कि अनुक्रम x (n) के DFT को X (K) द्वारा निरूपित किया जाता है। अब, यदि x (n) और X (K) जटिल मूल्यवान अनुक्रम हैं, तो इसे निम्न के रूप में दर्शाया जा सकता है
$x(n) = x_R(n)+jx_1(n),0\leq n\leq N-1$
तथा $X(K) = X_R(K)+jX_1(K),0\leq K\leq N-1$
द्वैत संपत्ति
आइए एक सिग्नल x (n) पर विचार करें, जिसका DFT X (K) के रूप में दिया गया है। बता दें कि परिमित अवधि अनुक्रम एक्स (एन) है। फिर द्वंद्व प्रमेय के अनुसार,
अगर, $x(n)\longleftrightarrow X(K)$
फिर, $X(N)\longleftrightarrow Nx[((-k))_N]$
इसलिए, इस प्रमेय का उपयोग करके यदि हम डीएफटी को जानते हैं, तो हम आसानी से परिमित अवधि अनुक्रम पा सकते हैं।
जटिल संयुग्म गुण
मान लीजिए, एक संकेत x (n) है, जिसका DFT हमें X (K) के रूप में भी जाना जाता है। अब, यदि संकेत के जटिल संयुग्म को x * (n) के रूप में दिया जाता है, तो हम नीचे दिखाए गए प्रमेय का उपयोग करके बहुत अधिक गणना किए बिना आसानी से डीएफटी पा सकते हैं।
अगर, $x(n)\longleftrightarrow X(K)$
फिर, $x*(n)\longleftrightarrow X*((K))_N = X*(N-K)$
सर्कुलर फ्रीक्वेंसी शिफ्ट
जटिल घातीय अनुक्रम के साथ अनुक्रम x (n) का गुणन $e^{j2\Pi kn/N}$आवृत्ति में L इकाइयों द्वारा DFT के गोलाकार बदलाव के बराबर है। यह सर्कुलर टाइम शिफ्टिंग प्रॉपर्टी के लिए दोहरी है।
अगर, $x(n)\longleftrightarrow X(K)$
फिर, $x(n)e^{j2\Pi Kn/N}\longleftrightarrow X((K-L))_N$
दो अनुक्रमों का गुणा
यदि दो सिग्नल x 1 (n) और x 2 (n) हैं और उनके संबंधित DFT X 1 (k) और X 2 (K) हैं, तो समय अनुक्रम में संकेतों का गुणा उनके DFT के परिपत्र कनवल्शन से मेल खाता है।
अगर, $x_1(n)\longleftrightarrow X_1(K)\quad\&\quad x_2(n)\longleftrightarrow X_2(K)$
फिर, $x_1(n)\times x_2(n)\longleftrightarrow X_1(K)© X_2(K)$
पारसेवल की प्रमेय
सामान्य रूप से जटिल मूल्यवान अनुक्रम x (n) और y (n) के लिए
अगर, $x(n)\longleftrightarrow X(K)\quad \&\quad y(n)\longleftrightarrow Y(K)$
फिर, $\sum_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\sum_{k = 0}^{N-1}X(K)Y^*(K)$
हम जानते हैं कि जब $\omega = 2\pi K/N$ तथा $N\rightarrow \infty,\omega$ एक सतत चर बन जाता है और सीमा योग बन जाता है $-\infty$ सेवा $+\infty$।
इसलिए,
$$NC_k = X(\frac{2\pi}{N}k) = X(e^{j\omega}) = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{\frac{-j2\pi nk}{N}} = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{-j\omega n}$$असतत समय फूरियर रूपांतरण (DTFT)
हम जानते हैं कि, $X(e^{j\omega}) = \sum_{n = -\infty}^\infty x(n)e^{-j\omega n}$
कहाँ पे, $X(e^{j\omega})$निरंतर और आवधिक है ω और अवधि 2 and के साथ। ... eq (1)
अभी,
$x_p(n) = \sum_{k = 0}^{N-1}NC_ke^{j2 \pi nk/N}$ ... फूरियर श्रृंखला से
$x_p(n) = \frac{1}{2\pi}\sum_{k=0}^{N-1}NC_ke^{j2\pi nk/N}\times \frac{2\pi}{N}$
and निरंतर और हो जाता है $\frac{2\pi}{N}\rightarrow d\omega$, उपरोक्त कारणों के कारण।
$x(n) = \frac{1}{2\pi}\int_{n = 0}^{2\pi}X(e^{j\omega})e^{j\omega n}d\omega$... eq (2)
प्रतिलोम असतत समय फूरियर रूपांतरण
प्रतीकात्मक,
$x(n)\Longleftrightarrow x(e^{j\omega})$(फूरियर ट्रांसफॉर्म जोड़ी)
गैर-आवधिक अनुक्रम x (n) के लिए असतत समय फूरियर रूपांतरण के अस्तित्व के लिए आवश्यक और पर्याप्त स्थिति पूर्ण योग है।
अर्थात$\sum_{n = -\infty}^\infty|x(n)|<\infty$
DTFT के गुण
Linearity : $a_1x_1(n)+a_2x_2(n)\Leftrightarrow a_1X_1(e^{j\omega})+a_2X_2(e^{j\omega})$
Time shifting - $x(n-k)\Leftrightarrow e^{-j\omega k}.X(e^{j\omega})$
Time Reversal - $x(-n)\Leftrightarrow X(e^{-j\omega})$
Frequency shifting - $e^{j\omega _0n}x(n)\Leftrightarrow X(e^{j(\omega -\omega _0)})$
Differentiation frequency domain - $nx(n) = j\frac{d}{d\omega}X(e^{j\omega})$
Convolution - $x_1(n)*x_2(n)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Multiplication - $x_1(n)\times x_2(n)\Leftrightarrow X_1(e^{j\omega})*X_2(e^{j\omega})$
Co-relation - $y_{x_1\times x_2}(l)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Modulation theorem - $x(n)\cos \omega _0n = \frac{1}{2}[X_1(e^{j(\omega +\omega _0})*X_2(e^{jw})$
Symmetry -$x^*(n)\Leftrightarrow X^*(e^{-j\omega})$ ;
$x^*(-n)\Leftrightarrow X^*(e^{j\omega})$ ;
$Real[x(n)]\Leftrightarrow X_{even}(e^{j\omega})$ ;
$Imag[x(n)]\Leftrightarrow X_{odd}(e^{j\omega})$ ;
$x_{even}(n)\Leftrightarrow Real[x(e^{j\omega})]$ ;
$x_{odd}(n)\Leftrightarrow Imag[x(e^{j\omega})]$ ;
Parseval’s theorem - $\sum_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$
इससे पहले, हमने आवृत्ति डोमेन में नमूने का अध्ययन किया। उस बुनियादी ज्ञान के साथ, हम नमूना लेते हैं$X(e^{j\omega})$आवृत्ति डोमेन में, ताकि उस सैंपल किए गए डेटा से एक सुविधाजनक डिजिटल विश्लेषण किया जा सके। इसलिए, DFT को समय और आवृत्ति डोमेन दोनों में नमूना लिया जाता है। धारणा के साथ$x(n) = x_p(n)$
इसलिए, DFT द्वारा दिया गया है -
$X(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{-\frac{j2\pi nk}{N}}$, k = 0,1,…।, N e 1 … eq (3)
और IDFT द्वारा दिया गया है -
$X(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k)e^{\frac{j2\pi nk}{N}}$, n = 0,1,…।, N e 1 … eq (4)
$\therefore x(n)\Leftrightarrow X(k)$
ट्विडल फैक्टर
इसे के रूप में चिह्नित किया जाता है $W_N$ और के रूप में परिभाषित किया गया $W_N = e^{-j2\pi /N}$। इसकी विशालता हमेशा एकता में बनी रहती है। का चरण$W_N = -2\pi /N$। यह यूनिट सर्कल पर एक वेक्टर है और इसका उपयोग कम्प्यूटेशनल सुविधा के लिए किया जाता है। गणितीय रूप से, इसे इस प्रकार दिखाया जा सकता है -
$W_N^r = W_N^{r\pm N} = W_N^{r\pm 2N} = ...$
यह r और अवधि N का कार्य है।
एन = 8, आर = 0,1,2,3,… .14,15,16,… पर विचार करें।
$\Longleftrightarrow W_8^0 = W_8^8 = W_8^{16} = ... = ... = W_8^{32} = ... =1= 1\angle 0$
$W_8^1 = W_8^9 = W_8^{17} = ... = ... = W_8^{33} = ... =\frac{1}{\sqrt 2}= j\frac{1}{\sqrt 2} = 1\angle-\frac{\pi}{4}$
रैखिक परिवर्तन
आइए हम समझते हैं रैखिक परिवर्तन -
हम जानते हैं कि,
$DFT(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \sum_{n = 0}^{N-1}x(n).W_n^{-nk};\quad k = 0,1,….,N−1$
$x(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k).W_N^{-nk};\quad n = 0,1,….,N−1$
Note- डीएफटी की गणना एन 2 जटिल गुणा और एन (एन -1) जटिल जोड़ के साथ किया जा सकता है ।
$x_N = \begin{bmatrix}x(0)\\x(1)\\.\\.\\x(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad x_N$
$X_N = \begin{bmatrix}X(0)\\X(1)\\.\\.\\X(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad X_N$
$\begin{bmatrix}1 & 1 & 1 & ... & ... & 1\\1 & W_N & W_N^2 & ... & ... & W_N^{N-1}\\. & W_N^2 & W_N^4 & ... & ... & W_N^{2(N-1)}\\.\\1 & W_N^{N-1} & W_N^{2(N-1)} & ... & ... & W_N^{(N-1)(N-1)} \end{bmatrix}$
मैट्रिक्स शब्द में N - बिंदु DFT द्वारा दिया गया है - $X_N = W_Nx_N$
$W_N\longmapsto$ रैखिक परिवर्तन का मैट्रिक्स
$Now,\quad x_N = W_N^{-1}X_N$
मैट्रिक्स फॉर्म में IDFT द्वारा दिया जाता है
$$x_N = \frac{1}{N}W_N^*X_N$$के दोनों भावों की तुलना करना $x_N,\quad W_N^{-1} = \frac{1}{N}W_N^*$ तथा $W_N\times W_N^* = N[I]_{N\times N}$
इसलिए, $W_N$ एक रैखिक परिवर्तन मैट्रिक्स, एक ऑर्थोगोनल (एकात्मक) मैट्रिक्स है।
की आवधिक संपत्ति से $W_N$ और इसकी सममित संपत्ति से, यह निष्कर्ष निकाला जा सकता है कि, $W_N^{k+N/2} = -W_N^k$
वृत्ताकार समरूपता
N ,L की परिमित अवधि x (n) के N- बिंदु DFT, x (n) के आवधिक विस्तार के N- बिंदु DFT के बराबर है, अर्थात $x_p(n)$ की अवधि एन। और $x_p(n) = \sum_{l = -\infty}^\infty x(n-Nl)$। अब, यदि हम अनुक्रम को स्थानांतरित करते हैं, जो कि कश्मीर इकाइयों द्वारा दाईं ओर एक आवधिक अनुक्रम है, तो एक और आवधिक अनुक्रम प्राप्त होता है। यह परिपत्र पारी के रूप में जाना जाता है और इस द्वारा दिया जाता है,
$$x_p^\prime (n) = x_p(n-k) = \sum_{l = -\infty}^\infty x(n-k-Nl)$$नए परिमित अनुक्रम का प्रतिनिधित्व किया जा सकता है
$$x_p^\prime (n) = \begin{cases}x_p^\prime(n), & 0\leq n\leq N-1\\0 & Otherwise\end{cases}$$Example - x (n) = {1,2,4,3}, N = 4,
$x_p^\prime (n) = x(n-k,modulo\quad N)\equiv x((n-k))_N\quad;ex-if\quad k=2i.e\quad 2\quad unit\quad right\quad shift\quad and\quad N = 4,$
सकारात्मक दिशा के रूप में दक्षिणावर्त दिशा मान ली गई।
हमें मिला, $x\prime(n) = x((n-2))_4$
$x\prime(0) = x((-2))_4 = x(2) = 4$
$x\prime(1) = x((-1))_4 = x(3) = 3$
$x\prime(2) = x((-2))_4 = x(0) = 1$
$x\prime(3) = x((1))_4 = x(1) = 2$
Conclusion - एन-पॉइंट अनुक्रम की परिपत्र पारी इसके आवधिक विस्तार और इसके विपरीत की एक रैखिक पारी के बराबर है।
अनुक्रमिक रूप से भी अनुक्रम - $x(N-n) = x(n),\quad 1\leq n\leq N-1$
$i.e.x_p(n) = x_p(-n) = x_p(N-n)$
सम्मिलित करें -$x_p(n) = x_p^*(N-n)$
परिपत्र विषम अनुक्रम - $x(N-n) = -x(n),\quad 1\leq n\leq N-1$
$i.e.x_p(n) = -x_p(-n) = -x_p(N-n)$
आकस्मिक विषम - $x_p(n) = -x_p^*(N-n)$
अभी, $x_p(n) = x_{pe}+x_{po}(n)$, कहाँ पे,
$x_{pe}(n) = \frac{1}{2}[x_p(n)+x_p^*(N-n)]$
$x_{po}(n) = \frac{1}{2}[x_p(n)-x_p^*(N-n)]$
किसी भी वास्तविक संकेत x (n) के लिए,$X(k) = X^*(N-k)$
$X_R(k) = X_R(N-k)$
$X_l(k) = -X_l(N-k)$
$\angle X(k) = -\angle X(N-K)$
Time reversal- 0 वें नमूने के बारे में नमूना उलट । इसे इस प्रकार दिया गया है;
$x((-n))_N = x(N-n),\quad 0\leq n\leq N-1$
समय उलट क्रम के नमूनों की साजिश रच रहा है, दक्षिणावर्त दिशा में अर्थात नकारात्मक दिशा ग्रहण की।
कुछ अन्य महत्वपूर्ण गुण
अन्य महत्वपूर्ण आईडीएफटी गुण $x(n)\longleftrightarrow X(k)$
Time reversal - $x((-n))_N = x(N-n)\longleftrightarrow X((-k))_N = X(N-k)$
Circular time shift - $x((n-l))_N \longleftrightarrow X(k)e^{j2\pi lk/N}$
Circular frequency shift - $x(n)e^{j2\pi ln/N} \longleftrightarrow X((k-l))_N$
Complex conjugate properties -
$x^*(n)\longleftrightarrow X^*((-k))_N = X^*(N-k)\quad and$
$x^*((-n))_N = x^*(N-n)\longleftrightarrow X^*(-k)$
Multiplication of two sequence -
$x_1(n)\longleftrightarrow X_1(k)\quad and\quad x_2(n)\longleftrightarrow X_2(k)$
$\therefore x_1(n)x_2(n)\longleftrightarrow X_1(k)\quadⓃ X_2(k)$
Circular convolution - और दो डीएफटी का गुणा
$x_1(k)\quad Ⓝ x_2(k) =\sum_{k = 0}^{N-1}x_1(n).x_2((m-n))_n,\quad m = 0,1,2,... .,N-1 $
$x_1(k)\quad Ⓝ x_2(k)\longleftrightarrow X_1(k).X_2(k)$
Circular correlation - अगर $x(n)\longleftrightarrow X(k)$ तथा $y(n)\longleftrightarrow Y(k)$ , तो वहाँ मौजूद है एक क्रॉस सहसंबंध अनुक्रम के रूप में चिह्नित $\bar Y_{xy}$ ऐसा है कि $\bar Y_{xy}(l) = \sum_{n = 0}^{N-1}x(n)y^*((n-l))_N = X(k).Y^*(k)$
Parseval’s Theorem - अगर $x(n)\longleftrightarrow X(k)$ तथा $y(n)\longleftrightarrow Y(k)$;
$\displaystyle\sum\limits_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\displaystyle\sum\limits_{n =0}^{N-1}X(k).Y^*(k)$
आइए हम दो परिमित अवधि क्रम x 1 (n) और x 2 (n) लेते हैं , पूर्णांक लंबाई N के रूप में रखते हैं। उनके DFT क्रमशः X 1 (K) और X 2 (K) हैं, जो नीचे दिखाया गया है -
$$X_1(K) = \sum_{n = 0}^{N-1}x_1(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$ $$X_2(K) = \sum_{n = 0}^{N-1}x_2(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$अब, हम दूसरे क्रम x 3 (n) के DFT को खोजने का प्रयास करेंगे , जिसे X 3 (K) के रूप में दिया गया है।
$X_3(K) = X_1(K)\times X_2(K)$
ऊपर के IDFT को लेने से हम प्राप्त करते हैं
$x_3(n) = \frac{1}{N}\displaystyle\sum\limits_{n = 0}^{N-1}X_3(K)e^{\frac{j2\Pi kn}{N}}$
उपरोक्त समीकरण को हल करने के बाद, आखिरकार, हम प्राप्त करते हैं
$x_3(n) = \displaystyle\sum\limits_{m = 0}^{N-1}x_1(m)x_2[((n-m))_N]\quad m = 0,1,2...N-1$
| तुलना अंक | रैखिक रूपांतरण | सर्कुलर कन्वेंशन |
|---|---|---|
| स्थानांतरण | रैखिक स्थानांतरण | परिपत्र स्थानांतरण |
| परिणय परिणाम में नमूने | $N_1+N_2−1$ | $Max(N_1,N_2)$ |
| एक फिल्टर की प्रतिक्रिया ढूँढना | मुमकिन | शून्य गद्दी के साथ संभव |
सर्कुलर कन्वेंशन के तरीके
आम तौर पर, दो विधियाँ हैं, जिन्हें परिपत्र कनवल्शन करने के लिए अपनाया जाता है और वे हैं -
- कंसेंट्रिक सर्कल विधि,
- मैट्रिक्स गुणन विधि।
कंसेंट्रिक सर्कल विधि
लश्कर $x_1(n)$ तथा $x_2(n)$दो दिए गए क्रम हो। के परिपत्र सजा के लिए कदम का पालन किया$x_1(n)$ तथा $x_2(n)$ कर रहे हैं
दो संकेंद्रित मंडलियां लें। के प्लॉट एन सैंपल$x_1(n)$ बाहरी घेरे की परिधि पर (समान दूरी के क्रमिक बिंदुओं को बनाए रखते हुए) एंटी-क्लॉकवाइज दिशा में।
साजिश रचने के लिए $x_2(n)$, के एन नमूने के आधार पर $x_2(n)$आंतरिक चक्र पर दक्षिणावर्त दिशा में, उसी बिंदु पर रखा गया नमूना जिसे 0 वें नमूने के रूप में रखा गया है$x_1(n)$
दो हलकों पर संबंधित नमूनों को गुणा करें और उन्हें आउटपुट प्राप्त करने के लिए जोड़ें।
एक बार में एक नमूने के साथ आंतरिक चक्र विरोधी घड़ी को घुमाएं।
मैट्रिक्स गुणन विधि
मैट्रिक्स विधि दो दिए गए अनुक्रम का प्रतिनिधित्व करती है $x_1(n)$ तथा $x_2(n)$ मैट्रिक्स रूप में।
दिए गए अनुक्रमों में से एक NXN मैट्रिक्स बनाने के लिए एक समय में एक नमूने के परिपत्र बदलाव के माध्यम से दोहराया जाता है।
अन्य अनुक्रम को कॉलम मैट्रिक्स के रूप में दर्शाया गया है।
दो मैट्रिसेस का गुणा सर्कुलर कनविक्शन का परिणाम देता है।
डीएफटी समय डोमेन कनवल्शन के लिए एक वैकल्पिक दृष्टिकोण प्रदान करता है। इसका उपयोग फ़्रीक्वेंसी डोमेन में रैखिक फ़िल्टरिंग करने के लिए किया जा सकता है।
इस प्रकार,$Y(\omega) = X(\omega).H(\omega)\longleftrightarrow y(n)$।
इस आवृत्ति डोमेन दृष्टिकोण में समस्या यह है कि $Y(\omega)$, $X(\omega)$ तथा $H(\omega)$are का निरंतर कार्य कर रहे हैं, जो कंप्यूटर पर डिजिटल गणना के लिए उपयोगी नहीं है। हालांकि, DFT उद्देश्य को हल करने के लिए इन तरंगों का नमूना संस्करण प्रदान करता है।
इसका लाभ यह है कि, एफएफटी की तरह तेजी से डीएफटी तकनीकों का ज्ञान होने से, समय-समय पर दृष्टिकोण के साथ तुलना में डिजिटल कंप्यूटर कम्प्यूटेशन के लिए एक कम्प्यूटेशनल रूप से उच्च कुशल एल्गोरिदम विकसित किया जा सकता है।
एक परिमित अवधि अनुक्रम पर विचार करें, $[x(n) = 0,\quad for,n<0\quad and\quad n\geq L]$ (सामान्यीकृत समीकरण), आवेग प्रतिक्रिया के साथ एक रैखिक फिल्टर को उत्तेजित करता है $[h(n) = 0,\quad forn<0\quad and\quad n\geq M]$।
$$x(n)y(n)$$ $$output = y(n) = \sum_{k = 0}^{M-1}h(k).x(n-k)$$दृढ़ संकल्प विश्लेषण से, यह स्पष्ट है कि, y (n) की अवधि L + M। 1 है।
फ़्रीक्वेंसी डोमेन में,
$$Y(\omega) = X(\omega).H(\omega)$$अभी, $Y(\omega)$ at का एक सतत कार्य है और इसे अलग-अलग नमूनों की संख्या के साथ असतत आवृत्तियों के एक सेट पर नमूना किया जाता है जो कि या उसके बराबर होना चाहिए $L+M-1$।
$$DFT\quad size = N\geq L+M-1$$साथ में $\omega = \frac{2\pi}{N}k$,
$Y(\omega) = X(k).H(k)$, जहां k = 0,1,…।, N-1
जहाँ, X (k) और H (k) क्रमशः x (n) और h (n) के N-बिंदु DFT हैं। $x(n)\& h(n)$ लंबाई के साथ शून्य तक गद्देदार हैं। यह निरंतर स्पेक्ट्रा को विकृत नहीं करेगा $X(\omega)$ तथा $H(\omega)$। जबसे$N\geq L+M-1$, उत्पादन क्रम y (n) के N- बिंदु DFT आवृत्ति डोमेन में y (n) का प्रतिनिधित्व करने के लिए पर्याप्त है और ये तथ्य अनुमान लगाते हैं कि X (k) और H (k) के N-बिंदु DFTs का गुणन, उसके बाद गणना एन-पॉइंट आईडीएफटी की उपज y (n) होनी चाहिए।
इसका तात्पर्य है, शून्य अंकन के साथ x (n) और H (n) का N- बिंदु वृत्ताकार विक्षेपण, x (n) और h (n) के रेखीय अभिसरण के बराबर है।
इस प्रकार, डीएफटी का उपयोग रैखिक फ़िल्टरिंग के लिए किया जा सकता है।
Caution - एन हमेशा से अधिक या बराबर होना चाहिए $L+M-1$। अन्यथा, अलियासिंग प्रभाव आउटपुट अनुक्रम को दूषित करेगा।
मान लीजिए, लंबी अवधि के इनपुट अनुक्रम x (n) को एक सिस्टम के साथ संसाधित किया जाना है जिसमें दो अनुक्रमों को हल करके परिमित अवधि आवेग प्रतिक्रिया है। चूंकि, डीएफटी के माध्यम से किए गए रैखिक फ़िल्टरिंग में एक निश्चित आकार के डेटा ब्लॉक पर ऑपरेशन शामिल है, प्रसंस्करण से पहले इनपुट अनुक्रम को विभिन्न निश्चित आकार के डेटा ब्लॉक में विभाजित किया जाता है।
क्रमिक ब्लॉकों को तब एक समय में संसाधित किया जाता है और परिणाम शुद्ध परिणाम के लिए संयुक्त होते हैं।
चूंकि लंबी इनपुट अनुक्रम को अलग-अलग निश्चित आकार के खंडों में विभाजित करके सजा का प्रदर्शन किया जाता है, इसलिए इसे खंडित रूपांतरण कहा जाता है। एफआईआर फ़िल्टर प्रसंस्करण से पहले एक लंबे इनपुट अनुक्रम को निश्चित आकार के खंडों में विभाजित किया जाता है।
असतत सजा के मूल्यांकन के लिए दो विधियों का उपयोग किया जाता है -
Overlap-save method
Overlap-add method
ओवरलैप सेव मेथड
ओवरलैप-सेव एक बहुत लंबे सिग्नल x (n) और एक परिमित आवेग प्रतिक्रिया (FIR) फ़िल्टर h (n) के बीच असतत सजा का मूल्यांकन करने के लिए एक कुशल तरीके के लिए पारंपरिक नाम है। नीचे दिए गए ओवरलैप सेव विधि के चरण दिए गए हैं -
इनपुट डेटा ब्लॉक की लंबाई दें = N = L + M-1। इसलिए, DFT और IDFT लंबाई = N. प्रत्येक डेटा ब्लॉक पिछले ब्लॉक के M-1 डेटा बिंदुओं का पालन करता है, उसके बाद L नया डेटा बिंदुओं की लंबाई N = L + M-1 का डेटा अनुक्रम बनाता है।
सबसे पहले, एन-पॉइंट डीएफटी की गणना प्रत्येक डेटा ब्लॉक के लिए की जाती है।
(एल -1) शून्य को जोड़कर, एफआईआर फिल्टर की आवेग प्रतिक्रिया लंबाई में बढ़ जाती है और एन बिंदु डीएफटी की गणना और संग्रहीत किया जाता है।
दो N- बिंदु DFTs H (k) और X m (k) का गुणा : Y ( m (k) = H (k) .X m (k), जहां K = 0,1,2,… N-1
फिर, IDFT [Y ( m ((k)] = y (((n) = [y, m (0), y ( m (1), y ( m (2), ....... y ' मीटर (एम 1), वाई' मीटर (एम), ....... वाई ' मीटर (एन -1)]
(यहां, एन -1 = एल + एम -2)
पहले M-1 अंक अलियासिंग के कारण दूषित होते हैं और इसलिए, उन्हें छोड़ दिया जाता है क्योंकि डेटा रिकॉर्ड लंबाई N का है।
अंतिम एल बिंदु दृढ़ संकल्प के परिणामस्वरूप बिल्कुल समान हैं, इसलिए
y) m (n) = y m (n) जहां n = M, M + 1,… .N-1
उपनाम से बचने के लिए, प्रत्येक डेटा रिकॉर्ड के अंतिम M-1 तत्व सहेजे जाते हैं और ये बिंदु बाद के रिकॉर्ड को आगे बढ़ाते हैं और 1 सेंट M-1 तत्व बन जाते हैं।

आईडीएफटी के परिणाम, जहां पहले एम -1 अंक से परहेज किया जाता है, अलियासिंग और शेष एल बिंदुओं को शून्य करने के लिए रैखिक परिणाम के रूप में वांछित परिणाम का गठन होता है।
ओवरलैप जोड़ें विधि
ओवरलैप विधि का उपयोग करके असतत आक्षेप का पता लगाने के लिए नीचे दिए गए चरण हैं -
इनपुट डेटा ब्लॉक का आकार L होने दें। इसलिए, DFT और IDFT का आकार: N = L + M-1
प्रत्येक डेटा ब्लॉक को अंतिम रूप से M-1 शून्य के साथ जोड़ा जाता है।
एन-पॉइंट डीएफटी की गणना करें।

दो N- बिंदु DFTs गुणा किए जाते हैं: Y m (k) = H (k) .X m (k), जहां k = 0, 1,2,…।, N-1।
IDFT [Y m (k)] लंबाई N के ब्लॉक का उत्पादन करता है जो अलियासिंग से प्रभावित नहीं होते हैं क्योंकि DFT का आकार N = L + M-1 है और प्रत्येक के लिए M-1 शून्य जोड़कर N- बिंदुओं के अनुक्रम की लंबाई बढ़ा दी है खंड मैथा।
प्रत्येक ब्लॉक के अंतिम एम -1 अंक को ओवरलैप किया जाना चाहिए और सफल ब्लॉक के पहले एम -1 अंक में जोड़ा जाना चाहिए।
(कारण: प्रत्येक डेटा ब्लॉक M-1 शून्य के साथ समाप्त होता है)
इसलिए, इस विधि को ओवरलैप-ऐड विधि के रूप में जाना जाता है। इस प्रकार, हम प्राप्त करते हैं -
y (n) = {y 1 (0), y 1 (1), y 1 (2),… .., y 1 (L-1), y 1 (L) + y 2 (0), y 1 (L + 1) + y 2 (1),… .., y 1 (N-1) + y 2 (M-1), y 2 (M),… .. । ... ... ...}
DCT (असतत कोसाइन ट्रांसफॉर्म) एक एन-इनपुट अनुक्रम x (n), 0≤n≤N-1 है, जो रैखिक परिवर्तन या जटिल घातांक के संयोजन के रूप में है। परिणामस्वरूप, DFT गुणांक सामान्य रूप से जटिल होते हैं, भले ही x (n) वास्तविक हो।
मान लीजिए, हम एक ऑर्थोगोनल परिवर्तन का पता लगाने की कोशिश करते हैं जिसमें एन × एन संरचना है जिसने एक वास्तविक अनुक्रम x (n) को कोसाइन अनुक्रम के रैखिक संयोजन के रूप में व्यक्त किया है। हम पहले से ही जानते हैं कि -
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$
तथा $x(n) = \frac{1}{N}\sum_{k = 0}^{N-1}x(k)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$
यह संभव है यदि N बिंदु अनुक्रम x (n) वास्तविक और सम है। इस प्रकार,$x(n) = x(N-n),0\leq n \leq (N-1)$। परिणामी DFT ही वास्तविक है और यहां तक कि। इन बातों से यह स्पष्ट होता है कि हम संभवतः एक असतत कोसाइन ट्रांसफ़ॉर्म कर सकते हैं, किसी भी एन पॉइंट वास्तविक अनुक्रम के लिए अनुक्रम के 2N बिंदु डीएफटी को ले कर।
डीसीटी, मूल रूप से, छवि और भाषण प्रसंस्करण में उपयोग किया जाता है। इसका उपयोग छवियों और भाषण संकेतों के संपीड़न में भी किया जाता है।
$DFT[s(n)] = S(k) = \sum_{n = 0}^{2N-1}s(n)W_{2N}^{nk},\quad where\quad 0\leq k \leq 2N-1$
$S(k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)W_{2N}^{nk}+\displaystyle\sum\limits_{n = N}^{2N-1}x(2N-n-1)W_{2N}^{nk};\quad where\quad 0\leq k\leq 2N-1$
$\Rightarrow S(k) = W_{2N}^{-k/2}+\sum_{n = 0}^{N-1}x(n) [W_{2N}^{nk}W_{2N}^{k/2}+W_{2N}^{-nk}W_{2N}^{-k/2}];\quad where\quad 0\leq k\leq 2N-1$
$\Rightarrow S(k) = W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{N}(n+\frac{1}{2})k];\quad where\quad 0\leq k\leq 2N-1$
DCT द्वारा परिभाषित किया गया है,
$V(k) = 2\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{2}(n+\frac{1}{2})k]\quad where\quad 0\leq k\leq N-1$
$\Rightarrow V(k) = W_{2N}^{\frac{k}{2}}S(k)\quad or\quad S(k) = W_{2N}^{\frac{k}{2}}V(k),\quad where\quad 0\leq k\leq N-1$
$\Rightarrow V(k) = 2R[W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)W_{2N}^{nk}],\quad where\quad 0\leq k\leq N-1$
उदाहरण 1
अनुक्रम के पारसेवल प्रमेय को सत्यापित करें $x(n) = \frac{1^n}{4}u(n)$
Solution - $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$
एलएचएस $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2$
$= \displaystyle\sum\limits_{-\infty}^{\infty}x(n)x^*(n)$
$= \displaystyle\sum\limits_{-\infty}^\infty(\frac{1}{4})^{2n}u(n) = \frac{1}{1-\frac{1}{16}} = \frac{16}{15}$
आरएचएस $X(e^{j\omega}) = \frac{1}{1-\frac{1}{4}e-j\omega} = \frac{1}{1-0.25\cos \omega+j0.25\sin \omega}$
$\Longleftrightarrow X^*(e^{j\omega}) = \frac{1}{1-0.25\cos \omega-j0.25\sin \omega}$
गिना जा रहा है, $X(e^{j\omega}).X^*(e^{j\omega})$
$= \frac{1}{(1-0.25\cos \omega)^2+(0.25\sin \omega)^2} = \frac{1}{1.0625-0.5\cos \omega}$
$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega$
$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega = 16/15$
हम देख सकते हैं कि, LHS = RHS। (इसलिए साबित)
उदाहरण 2
के एन-पॉइंट डीएफटी की गणना करें $x(n) = 3\delta (n)$
Solution - हम जानते हैं कि,
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$
$= \displaystyle\sum\limits_{n = 0}^{N-1}3\delta(n)e^{\frac{j2\Pi kn}{N}}$
$ = 3\delta (0)\times e^0 = 1$
इसलिए,$x(k) = 3,0\leq k\leq N-1$… Ans।
उदाहरण 3
के एन-पॉइंट डीएफटी की गणना करें $x(n) = 7(n-n_0)$
Solution - हम जानते हैं कि,
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$
X (n) के मान को प्रतिस्थापित करते हुए,
$\displaystyle\sum\limits_{n = 0}^{N-1}7\delta (n-n_0)e^{-\frac{j2\Pi kn}{N}}$
$= e^{-kj14\Pi kn_0/N}$… Ans
पहले के डीएफटी तरीकों में, हमने देखा है कि कम्प्यूटेशनल भाग बहुत लंबा है। हम इसे कम करना चाहते हैं। यह एफएफटी या तेज फूरियर ट्रांसफॉर्म के माध्यम से किया जा सकता है। इसलिए, हम कह सकते हैं कि FFT एक एल्गोरिथम प्रारूप में असतत फूरियर रूपांतरण की गणना के अलावा कुछ भी नहीं है, जहां कम्प्यूटेशनल भाग कम हो जाएगा।
एफएफटी होने का मुख्य लाभ यह है कि इसके माध्यम से हम एफआईआर फिल्टर डिजाइन कर सकते हैं। गणितीय रूप से, एफएफटी को निम्नानुसार लिखा जा सकता है;
$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$इसे बेहतर तरीके से समझने के लिए एक उदाहरण लेते हैं। हमने नाम से आठ बिंदुओं पर विचार किया है$x_0\quad to\quad x_7$। हम एक समूह में समान शब्द और दूसरे में विषम शब्द चुनेंगे। ऊपर कहा गया है की आरेखीय दृश्य नीचे दिखाया गया है -
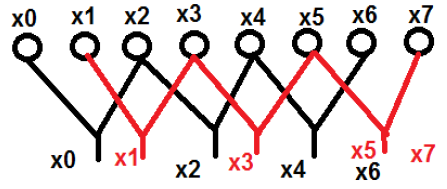
यहाँ, अंक x 0 , x 2 , x 4 और x 6 को एक श्रेणी में बांटा गया है और इसी तरह, अंक x 1 , x 3 , x 5 और x 7 को अन्य श्रेणी में रखा गया है। अब, हम उन्हें दो के समूह में आगे बना सकते हैं और संगणना के साथ आगे बढ़ सकते हैं। अब, देखते हैं कि कैसे आगे दो में टूटने से गणना में मदद मिल रही है।
$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$
$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$
$= G[k]+H[k]\times W_N^k$
शुरू में, हमने आठ-बिंदु क्रम लिया, लेकिन बाद में हमने उस एक को दो भागों में तोड़ दिया [जी] और एच [के]। G [k] का अर्थ सम भाग के लिए है जबकि H [k] विषम भाग के लिए है। यदि हम इसे आरेख के माध्यम से महसूस करना चाहते हैं, तो इसे नीचे दिखाया जा सकता है -
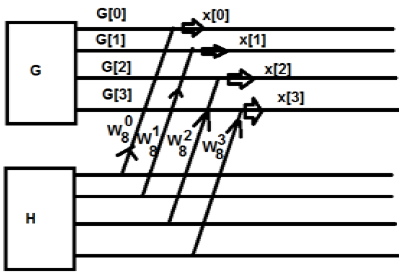
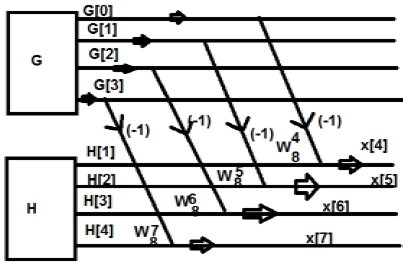
उपरोक्त आंकड़े से, हम यह देख सकते हैं
$W_8^4 = -1$
$W_8^5 = -W_8^1$
$W_8^6 = -W_8^2$
$W_8^7 = -W_8^3$
इसी प्रकार, अंतिम मान निम्न प्रकार लिखे जा सकते हैं -
$G[0]-H[0] = x[4]$
$G[1]-W_8^1H[1] = x[5]$
$G[2]-W_8^2H[2] = x[6]$
$G[1]-W_8^3H[3] = x[7]$
उपरोक्त एक आवधिक श्रृंखला है। इस प्रणाली का नुकसान यह है कि K को 4 बिंदु से परे नहीं तोड़ा जा सकता है। अब हम उपरोक्त को आगे तोड़ते हैं। हम संरचनाओं को कुछ इस तरह से प्राप्त करेंगे
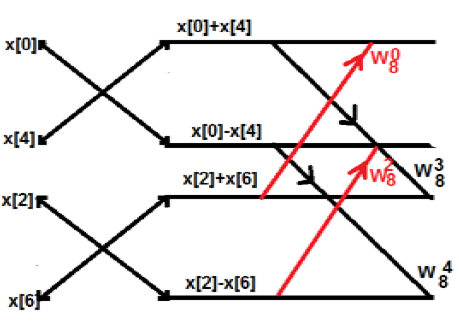
उदाहरण
अनुक्रम x [n] = {2,1, -1, -3,0,1,2,1} पर विचार करें। FFT की गणना करें।
Solution - दिया गया क्रम x [n] = {2,1, -1, -3,0,1,2,1} है
नीचे दिखाए अनुसार शब्दों को व्यवस्थित करें;
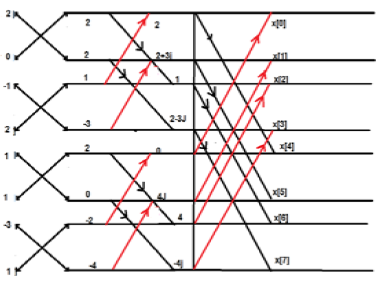
FFT की गणना करने के लिए तेजी से हार्डवेयर डिजाइन करने के लिए मेमोरी का यह कुशल उपयोग महत्वपूर्ण है। इस मेमोरी उपयोग का वर्णन करने के लिए इन-प्लेस अभिकलन शब्द का उपयोग किया जाता है।
समय अनुक्रम में गिरावट
इस संरचना में, हम द्विआधारी प्रारूप में 0 और 1 में सभी बिंदुओं का प्रतिनिधित्व करते हैं। फिर, हम उन संरचनाओं को उलट देते हैं। उसके बाद हमें जो क्रम मिलता है, उसे बिट रिवर्सल अनुक्रम के रूप में जाना जाता है। इसे समय क्रम में विघटन के रूप में भी जाना जाता है। एक आठ-सूत्रीय डीएफटी का इन-प्लेस संगणना एक सारणीबद्ध प्रारूप में दिखाया गया है जैसा कि नीचे दिखाया गया है -
| अंक | द्विआधारी प्रारूप | उलट | एक्वैरियम अंक |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
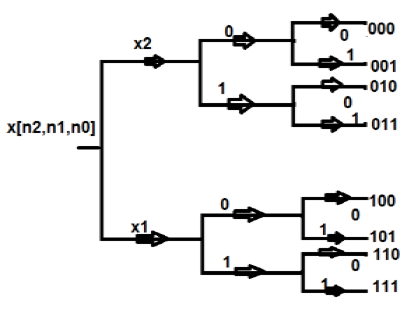
फ्रीक्वेंसी सीक्वेंस में गिरावट
समय अनुक्रम के अलावा, एन-पॉइंट अनुक्रम को आवृत्ति में भी दर्शाया जा सकता है। इसे बेहतर तरीके से समझने के लिए हम चार सूत्री क्रम लेते हैं।
अनुक्रम होने दो $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$। हम शुरू में दो बिंदुओं को एक समूह में बाँटेंगे। गणितीय रूप से, इस क्रम को इस प्रकार लिखा जा सकता है;
$$x[k] = \sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$अब हम क्रम संख्या ० से ३ का एक समूह बनाते हैं और क्रम ४ से group से group तक एक और समूह बनाते हैं। गणितीय रूप से इसे इस प्रकार दिखाया जा सकता है;
$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[n]W_N^{nk}+\displaystyle\sum\limits_{n = N/2}^{N-1}x[n]W_N^{nk}$$N से r को प्रतिस्थापित करते हैं, जहाँ r = 0, 1, 2…। (N / 2-1)। गणित के अनुसार,
$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[r]W_{N/2}^{nr}$$हम शुरू में पहले चार अंक (x [0], x [1], x [2], x [3]) लेते हैं और निम्नानुसार गणितीय रूप से उनका प्रतिनिधित्व करने का प्रयास करते हैं -
$\sum_{n = 0}^3x[n]W_8^{nk}+\sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$
$= \lbrace \sum_{n = 0}^3x[n]+\sum_{n = 0}^3x[n+4]W_8^{(4)k}\rbrace \times W_8^{nk}$
अभी $X[0] = \sum_{n = 0}^3(X[n]+X[n+4])$
$X[1] = \sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$
$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$
हम इसे दो और भागों में तोड़ सकते हैं, जिसका अर्थ है कि उन्हें 4-बिंदु अनुक्रम के रूप में तोड़ने के बजाय, हम उन्हें 2-बिंदु अनुक्रम में तोड़ सकते हैं।
एफआईआर फिल्टर फिल्टर के कंप्यूटर एडेड डिजाइन बनाने में उपयोगी हो सकते हैं। आइए एक उदाहरण लें और देखें कि यह कैसे काम करता है। नीचे दिए गए वांछित फिल्टर का एक आंकड़ा है।

कंप्यूटर डिजाइनिंग करते समय, हम पूरे निरंतर ग्राफ के आंकड़ों को असतत मानों में तोड़ देते हैं। कुछ सीमाओं के भीतर, हम असतत परिमाण वाले भागों की संख्या 64, 256 या 512 (और इसी तरह) तोड़ते हैं।
उपरोक्त उदाहरण में, हमने-above से + we के बीच की सीमाएँ ली हैं। हमने इसे 256 भागों में विभाजित किया है। अंक को H (0), H (1),… .up से H (256) के रूप में दर्शाया जा सकता है। यहां, हम IDFT एल्गोरिथ्म लागू करते हैं और यह हमें रैखिक चरण की विशेषताएं देगा।
कभी-कभी, हमें फ़िल्टर के कुछ विशेष क्रम में दिलचस्पी हो सकती है। हम कहते हैं कि हम 9 वें क्रम फ़िल्टर के माध्यम से ऊपर दिए गए डिज़ाइन को महसूस करना चाहते हैं । इसलिए, हम h0, h1, h2… .h9 के रूप में फ़िल्टर मान लेते हैं। गणितीय रूप से, इसे नीचे दिखाया जा सकता है
$$H(e^{j\omega}) = h_0+h_1e^{-j\omega}+h_2e^{-2j\omega}+.....+h_9e^{-9j\omega}$$जहां बड़ी संख्या में अव्यवस्थाएं हैं, हम अधिकतम अंक लेते हैं।
उदाहरण के लिए, उपरोक्त आकृति में, बिंदु B और C. के बीच अचानक से गिरावट होती है, इसलिए, हम इस बिंदु पर अधिक असतत मान लेने का प्रयास करते हैं, लेकिन बिंदु C और D के बीच एक निरंतर ढलान है। असतत मूल्यों की कम संख्या।
उपरोक्त फिल्टर को डिजाइन करने के लिए, हम निम्न प्रक्रिया से गुजरते हैं;
$H(e^{j\omega1}) = h_0+h_1e^{-j\omega1}+h_2e^{-2j\omega1}+.....+h_9e^{-9j\omega1}$
$H(e^{j\omega2}) = h_0+h_1e^{-j\omega2}+h_2e^{-2j\omega2}+.....+h_9e^{-9j\omega2}$
इसी तरह,
$(e^{j\omega1000}) = h_0+h_1eH^{-j\omega1000}h_2e^{-2j\omega1000}+.....+h_9+e^{-9j\omega1000}$
मैट्रिक्स समीकरण में उपरोक्त समीकरण का प्रतिनिधित्व, हमारे पास है -
$$\begin{bmatrix}H(e^{j\omega_1})\\.\\.\\H(e^{j\omega_{1000}}) \end{bmatrix} = \begin{bmatrix}e^{-j\omega_1} & ... & e^{-j9\omega_1} \\. & & . \\. & & . \\e^{-j\omega_{1000}} &... & e^{j9\omega_{1000}} \end{bmatrix}\begin{bmatrix}h_0\\.\\.\\h_9\end{bmatrix}$$आइए हम 1000 × 1 मैट्रिक्स को B, 1000 × 9 मैट्रिक्स को A और 9 × 1 मैट्रिक्स के रूप में लेते हैं $\hat{h}$।
तो, उपरोक्त मैट्रिक्स को हल करने के लिए, हम लिखेंगे
$\hat{h} = [A^TA]^{-1}A^{T}B$
$= [A^{*T}A]^{-1}A^{*T}B$
जहां A * मैट्रिक्स A के जटिल संयुग्म का प्रतिनिधित्व करता है।